学做网站要代码/dz论坛如何seo
9,图
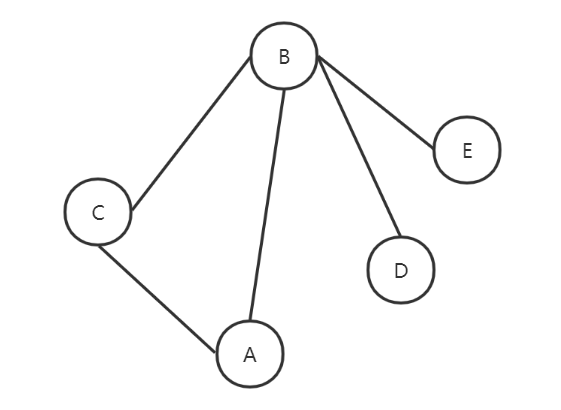
图是一种能够表示多对多关系的数据结构。
图的创建及表示方式:
1)邻接矩阵:用二维数组表示顶点之间的关系;
2)邻接表:因为邻接矩阵的表示方式会把每个顶点都分配n个空间,造成空间浪费,采用数组+链表的方式。
9.1,图的遍历:
1)深度优先遍历(Deep First Search,DFS)
首先访问第一个结点的邻接结点,然后以该邻接结点作为初始结点,继续访问它的第一个邻接结点。它是一个递归的过程。每次访问后都需要做个标记。可以看到,访问策略是优先纵向往深度挖掘。
思路:
1,访问初始结点V,并标记已访问;
2,查找结点V的第一个邻接结点w;
3,如果w存在,则继续执行步骤4,否则,回到步骤1,从v的下一个结点开始;
4,如果w没有访问,对w进行深度优先遍历(即递归执行123);
5,查找结点v的w的下一个邻接结点,回到步骤3。
核心代码:
int getFirstNeighbor(int index):用于找到初始结点的第一个邻接结点位置;
int getNeighbor(int v1,int v2):找到当前结点的邻接结点,v1、v2分别表示二维矩阵的i,j;
void dfs(boolean[] isVisted,int index):主方法,传入记录当前结点是否被访问的数组和当前结点下标;
public int getNeighbor(int index){//vertex,edges分别为顶点集合和边的二维数组for(int i =0;i<vertex.size();i++){if(edges[index][i]==1){return i;}return -1;}
}
public int getNeighbor(int v1,int v2){for(int j = v2+1;j<vertex.size();j++){if(edges[v1][j]==1){return j;}return -1;}
}
public void dfs(boolean[] isVisted,int index){sout("访问了->"+getVetrex(index));//标记为已访问isVisted[index] = true;//找到第一个邻接结点位置int w = getFirstNeighbor(int index);while(w!=-1){if(!isVisted[w]){dfs(isVisted,w);}w = getNeighbor(index,w);}
}
2)广度优先遍历(BFS,Broad First Search)
从第一个结点开始,试图遍历他的所有邻接结点值,直到遍历完。然后从开始的上一结点重复进行相似的动作。实则是分层遍历,此处运用了队列的结构。所以,它是优先广度遍历完相邻的结点。
思路:
1,访问初始结点并标记;
2,结点v入队;
3,队列非空,继续;否则结束当前算法;
4,出队列,取头结点u;
5,查找u的第一个邻接结点w;
6,若w不存在,回到步骤3;否则循环执行:
6.1,w未被访问,则访问并标记;
6.2,w入队
6.3,查找w的下一邻接结点w,回到步骤6。
核心代码:
private void bfs(boolean[] isVisited, int index){//定义对头位置和邻接结点int u;int w;System.out.print(getVertex(index)+"->");isVisited[index] = true;//构造一个队列LinkedList queue = new LinkedList();queue.addLast(index);while (!queue.isEmpty()){//出队u = (Integer) queue.removeFirst();w = getFirstNeighbor(u);while(w!=-1){if(!isVisited[w]){System.out.print(getVertex(w)+"->");isVisited[w] = true;queue.addLast(w);}w = getNeighbor(u,w);}}}
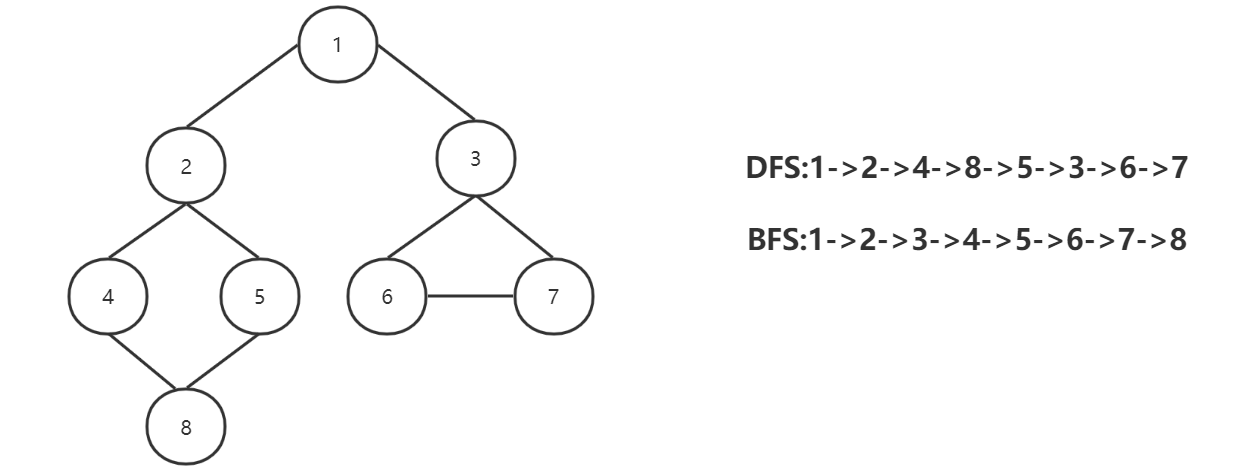
BFS和DFS的特点分析
对于遍历问题来说,二者是没有什么区别的,因为都要访问所有的结点。那么对于一些最短路径问题,二者或有不同:
- 时间复杂度上:BFS因为是以“面”的形式展开,各条路径是齐头并进,所以可能会在没有遍历完树的情况下,最先找到最短的路径;DFS依靠递归的形式遍历树,需要遍历完整棵树才知道结果。所以此时BFS由于DFS。虽然,他们的平均时间复杂度均为T(N)。
- 空间复杂度:在满二叉树的情况下,DFS的空间复杂度就是树的高度,为O(logN);BFS的空间复杂度就是树的叶子结点数列,为O(N/2)。所以此时DFS优于BFS。
