WordPress页脚添加日期/百度谷歌seo优化

数据结构与算法 二叉树

一、简述

       记--简单的有序链式二叉树添加、删除、遍历操作例子，有序：左孩子<父节点<右孩子。

二、例子

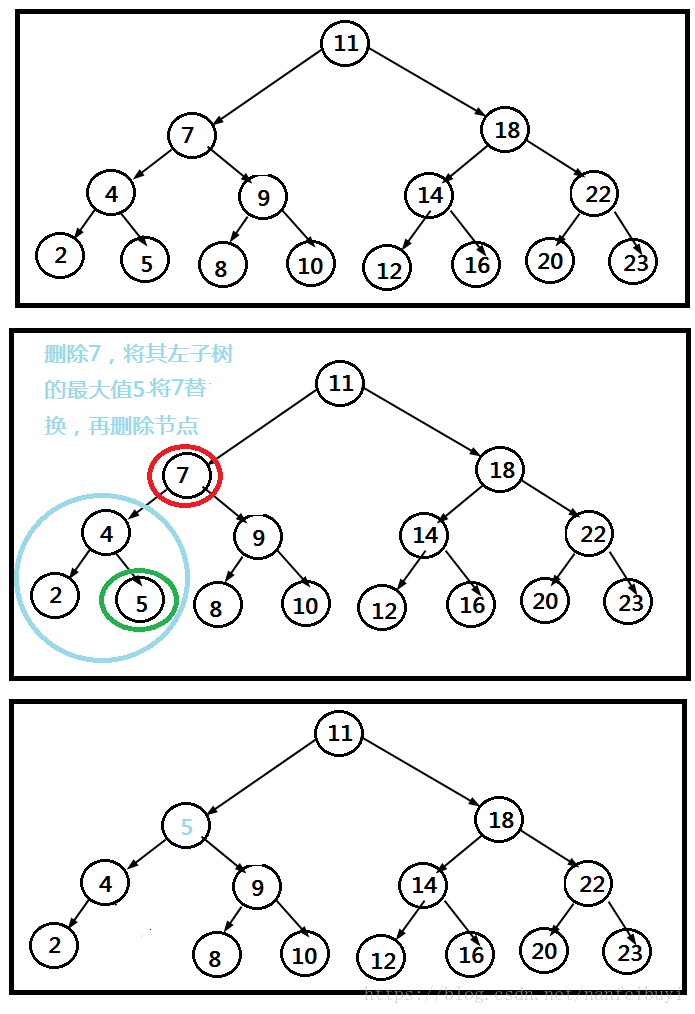
       输入正数就添加到二叉树，负数就删除对应的节点，输入0释放整个二叉树。例如输入7，就将7作为新的节点加到二叉树中，输入-7就将二叉树中的数据为7的节点删除。添加节点是会插入到响应顺序的位置，删除节点：如果是叶子节点（左右子树为NULL）就直接删除，要是有左子树，就将左子树的最大值B将要删除的节点A替换掉，再删除节点A，要是只有右子树，就将右子树的最大值C将删除的节点A替换掉，再删除节点A。

        

       测试代码：

#include <stdio.h>
#include <stdlib.h>//节点的定义
typedef struct bs_tree
{int data;struct bs_tree *lchild;struct bs_tree *rchild;
}TNode;TNode* m_root = NULL;//根节点TNode* create_node(int data)//创建节点
{TNode *new_node = (TNode*)malloc(sizeof(TNode));if(new_node == NULL){printf("%d:create new_node failed!\n",__LINE__);return NULL;}new_node->data = data;new_node->lchild = NULL;new_node->rchild = NULL;return new_node;
}TNode* add_node(TNode* root,TNode* new_node)//添加节点到合适的位置（满足 左<根<右）
{if(root == NULL){return new_node;}if(new_node->data > root->data)//新的节点大于当前节点，将新的节点添加到右子树{root->rchild = add_node(root->rchild,new_node);}else if(new_node->data < root->data)//新的节点小于当前节点，将新的节点添加到左子树{root->lchild = add_node(root->lchild,new_node);}return root;
}int indent(TNode* root,int data)//打印所有元素时缩进
{int ret;if(data == root->data){return 1;}if(data<root->data){if(root->lchild != NULL){ret = indent(root->lchild,data);if(ret == 0)//如果不是根节点，才打印{printf("|  ");}}}else{if(root->rchild != NULL){ret = indent(root->rchild,data);if(ret == 0)//如果不是根节点，才打印{printf("|  ");}}}return 0;
}
void display_tree(TNode* root)//打印所有元素
{int ret;if(root == NULL){return;}ret = indent(m_root,root->data);if(ret == 0)//如果不是根节点，才打印{printf("├──");}printf("%d \n",root->data);if(root->lchild != NULL){display_tree(root->lchild);}if(root->rchild != NULL){display_tree(root->rchild);}}TNode* free_tree(TNode* root)//释放内存空间
{if(root == NULL){return NULL;}if(root->lchild != NULL){root->lchild = free_tree(root->lchild);}if(root->rchild != NULL){root->rchild = free_tree(root->rchild);}if(root->lchild == NULL && root->rchild == NULL){printf("free=%d \n",root->data);free(root);return NULL;}return root;
}TNode*  remove_node(TNode* root,int data)//移除节点，并调整位置（满足 左<根<右）
{if(root == NULL){return NULL;}if(root->data == data){if(root->lchild == NULL && root->rchild == NULL){free(root);return NULL;}if(root->lchild != NULL){TNode* tp = NULL;for(tp = root->lchild;tp->rchild != NULL;tp = tp->rchild){}root->data = tp->data;root->lchild = remove_node(root->lchild,tp->data);}else if(root->rchild != NULL){TNode* tp = NULL;for(tp = root->rchild;tp->rchild != NULL;tp = tp->rchild){}root->data = tp->data;root->rchild = remove_node(root->rchild,tp->data);}return root;}if(root->lchild != NULL){root->lchild = remove_node(root->lchild,data);}if(root->rchild != NULL){root->rchild = remove_node(root->rchild,data);}return root;}int main(int argc,char* argv[])
{int data;TNode *root = NULL;TNode *new_node = NULL;while(1){scanf("%d",&data);if(data>0)//正数添加到树{new_node = create_node(data);root = add_node(root,new_node);m_root = root;printf("--------------------\n");display_tree(root);printf("--------------------\n\n\n");}else{if(data == 0)//退出程序{free_tree(root);break;}else //负数，移除对应的节点{root = remove_node(root,-data);m_root = root;printf("--------------------\n");display_tree(root);printf("--------------------\n");}}}return 0;
}

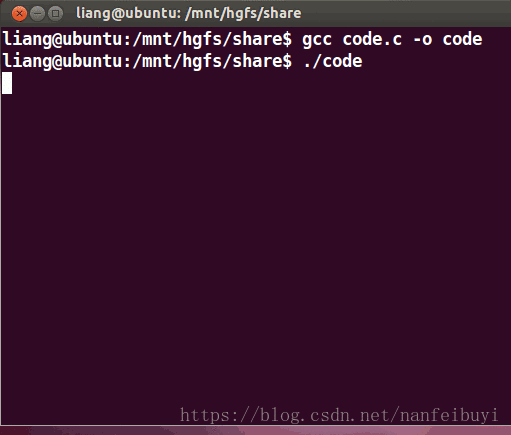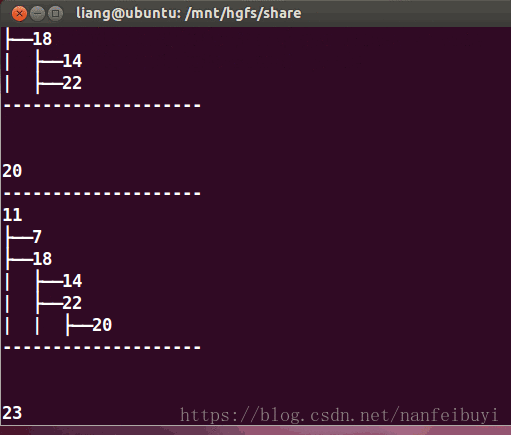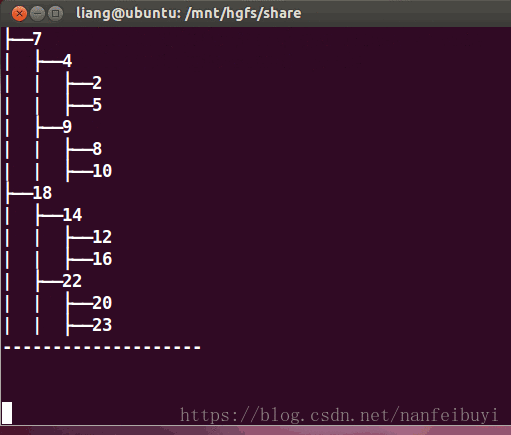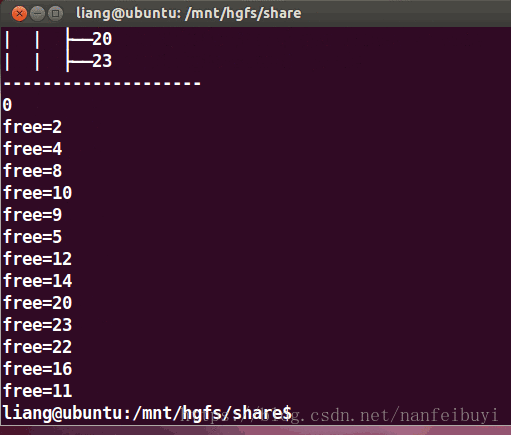
       测试结果：

                                    

      

三、二叉树的遍历

         

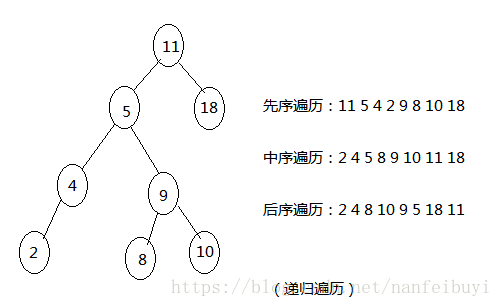
  先序遍历：先访问根节点，先序遍历左子树，先序遍历右子树。

  中序遍历： 中序遍历左子树，访问根节点，中序遍历右子树。

  后序遍历：后序遍历左子树，后序遍历右子树，访问根节点。

     图示：

                                        

     代码结构：

     测试代码：

#include <stdio.h>
#include <stdlib.h>//节点的定义
typedef struct bs_tree
{int data;struct bs_tree *lchild;struct bs_tree *rchild;
}TNode;TNode* m_root = NULL;//根节点TNode* create_node(int data)//创建节点
{TNode *new_node = (TNode*)malloc(sizeof(TNode));if(new_node == NULL){printf("%d:create new_node failed!\n",__LINE__);return NULL;}new_node->data = data;new_node->lchild = NULL;new_node->rchild = NULL;return new_node;
}TNode* add_node(TNode* root,TNode* new_node)//添加节点到合适的位置（满足 左<根<右）
{if(root == NULL){return new_node;}if(new_node->data > root->data)//新的节点大于当前节点，将新的节点添加到右子树{root->rchild = add_node(root->rchild,new_node);}else if(new_node->data < root->data)//新的节点小于当前节点，将新的节点添加到左子树{root->lchild = add_node(root->lchild,new_node);}return root;
}
/*根结点D、左子树L、右子树R*D=Degree*L=Left*R=Right*结点拥有的子树数称为结点的度（Degree）*根 (Root)*子树 (Sub Tree)*先序遍历: DLR*中序遍历；LDR*后续遍历：LRD*/void display_tree_DLR(TNode* root)//先序遍历
{if(root == NULL){return;}printf("%d ",root->data);if(root->lchild != NULL){display_tree_DLR(root->lchild);}if(root->rchild != NULL){display_tree_DLR(root->rchild);}}void display_tree_LDR(TNode* root)//中序遍历
{if(root == NULL){return;}if(root->lchild != NULL){display_tree_LDR(root->lchild);}printf("%d ",root->data);if(root->rchild != NULL){display_tree_LDR(root->rchild);}
}void display_tree_LRD(TNode* root)//后序遍历
{if(root == NULL){return;}if(root->lchild != NULL){display_tree_LRD(root->lchild);}if(root->rchild != NULL){display_tree_LRD(root->rchild);}printf("%d ",root->data);}TNode* free_tree(TNode* root)//释放内存空间
{if(root == NULL){return NULL;}if(root->lchild != NULL){root->lchild = free_tree(root->lchild);}if(root->rchild != NULL){root->rchild = free_tree(root->rchild);}if(root->lchild == NULL && root->rchild == NULL){printf("free=%d \n",root->data);free(root);return NULL;}return root;
}TNode*  remove_node(TNode* root,int data)//移除节点，并调整位置（满足 左<根<右）
{if(root == NULL){return NULL;}if(root->data == data){if(root->lchild == NULL && root->rchild == NULL)//没有孩子节点的直接移除{free(root);return NULL;}if(root->lchild != NULL){TNode* tp = NULL;for(tp = root->lchild;tp->rchild != NULL;tp = tp->rchild){}root->data = tp->data;root->lchild = remove_node(root->lchild,tp->data);}else if(root->rchild != NULL){TNode* tp = NULL;for(tp = root->rchild;tp->rchild != NULL;tp = tp->rchild){}root->data = tp->data;root->rchild = remove_node(root->rchild,tp->data);}return root;}if(root->lchild != NULL){root->lchild = remove_node(root->lchild,data);}if(root->rchild != NULL){root->rchild = remove_node(root->rchild,data);}return root;}int main(int argc,char* argv[])
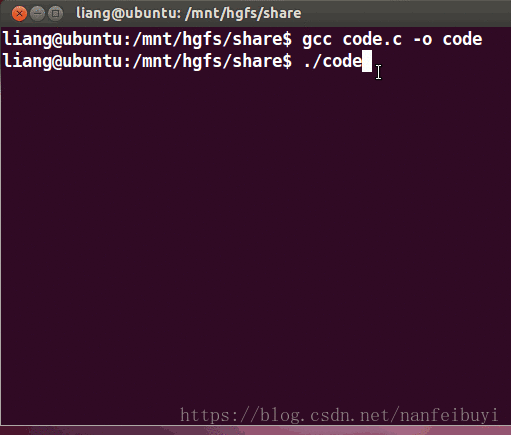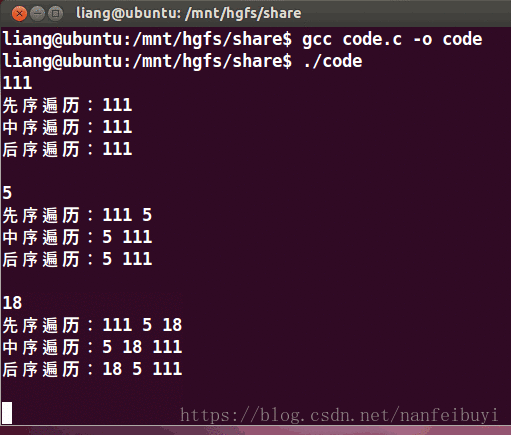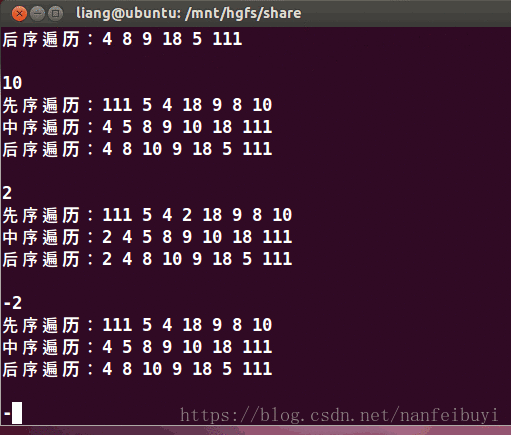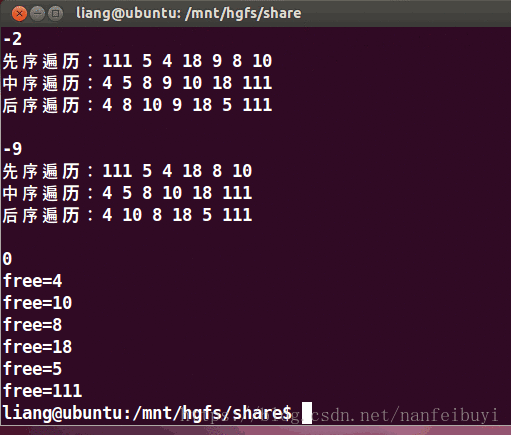
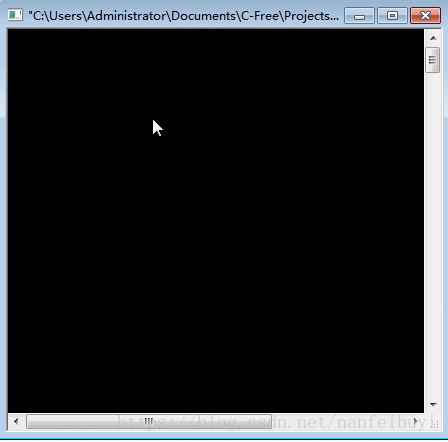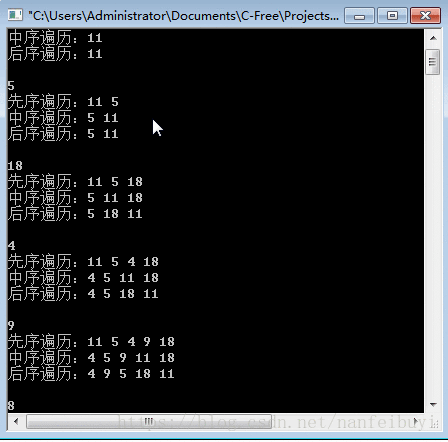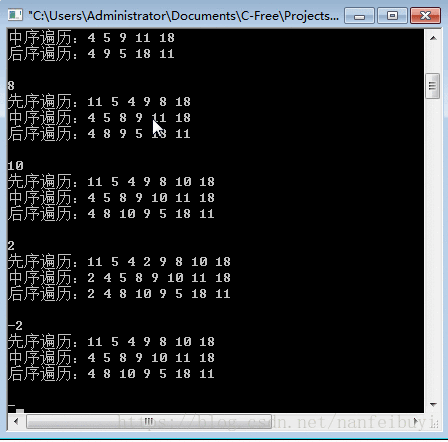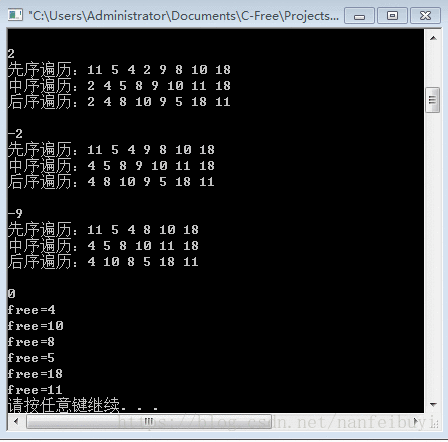
{int data;TNode *root = NULL;TNode *new_node = NULL;while(1){scanf("%d",&data);if(data>0)//正数添加到树{new_node = create_node(data);root = add_node(root,new_node);m_root = root;printf("先序遍历：");display_tree_DLR(root);printf("\n中序遍历：");display_tree_LDR(root);printf("\n后序遍历：");display_tree_LRD(root);printf("\n\n");}else{if(data == 0)//退出程序{free_tree(root);break;}else //负数，移除对应的节点{root = remove_node(root,-data);m_root = root;printf("先序遍历：");display_tree_DLR(root);printf("\n中序遍历：");display_tree_LDR(root);printf("\n后序遍历：");display_tree_LRD(root);printf("\n\n");}}}return 0;
}

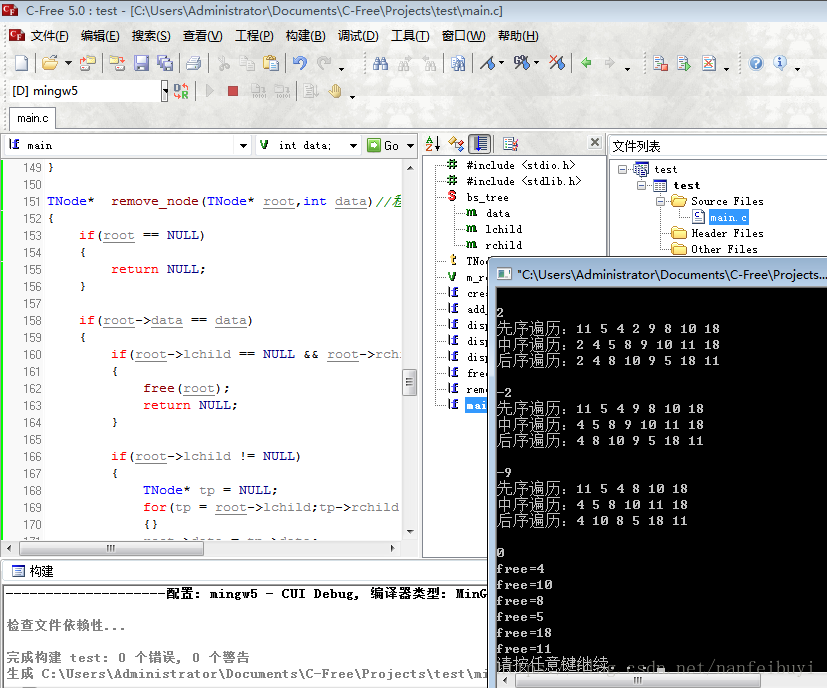
     运行结果：