【Matlab】

笔记开源：

关注微信公众号二进制人工智能并回复matlab,即可获取本文的md文件。
回复md,可获得md文件编辑器安装包，可对本文进行二次笔记。

A 数值微分与数值积分

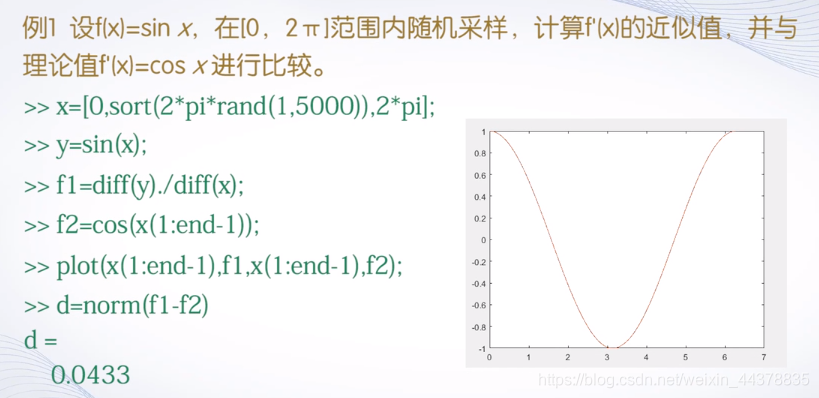
A.a数值微分(diff)

<1>数值差分与差商
任意函数$f(x)$在$x0$点的导数是通过极限定义的：

<2>数值微分的实现
MATLAB提供了求向前差分的函数diff，其调用格式有三种：

• dx=diff(x)：计算向量x的一阶向前差分，dx(i)=x(i+1)-x(i),i=1,2,...,n-1
• dx=diff(x, n) ：计算向量x的n阶向前差分。例如：diff(x, 2)=diff(diff(x))
• dx=diff(A,n,dim)：计算矩阵A的n阶差分，dim=1时（默认状态），按列计算差分；dim=2时，按行计算差分。

计算差分之后，可以计算$f（x）$在某点的差商，计算$f^{\prime }(x)$的近似值。
例子：

A.b 数值积分

<1>数值积分基本原理
牛顿-莱布尼茨公式：

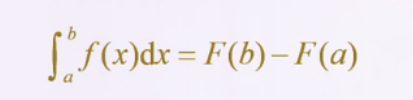
按积分区间[a, b]分成n个子区间$[x_i,x_{i+1}]，i=1,2,...,n$，其中$x_1=a,x_{n+1}=b$，这样求定积分的问题就分解为下面的求和问题：

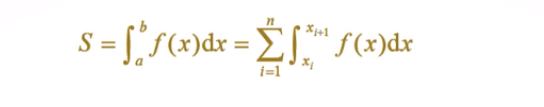
<2>数值积分的实现

• 基于自适应辛普森方法：[l.n]=quad(filename, a, b, tol, trace)
• 基于自适应Gauss-Lobatto方法：[l, n]=quadl(filename, a,b,tol, trace)

其中，filename是被积函数名；a和b分别是定积分的上限和下限，积分限[a, b]必须是有限的，不能是无穷大；tol用来控制积分精度，默认时取$tol=10^{-6}$；trace控制是否展现积分过程，若取非0则展现积分过程，取0则不展现，默认trace=0；返回参数I即定积分的值。n为被积函数的调用次数。

例子：

• 基于全局自适应积分方法
  I=integral(filename,a,b)
  其中，I是计算得到的积分；filename是被积函数；a和b分别是定积分的下限和上限，积分限可以是无穷大。

• 基于自适应高斯-克朗罗德方法
  [I,err]=quadgk(filename, a, b)
  其中，err返回近似误差范围，其他参数的含义和用法与quad函数想相同。积分上下限可以是无穷大，也可以是复数。如果积分上下限为复数，则quadgk函数在复平面上求积分。

例子：

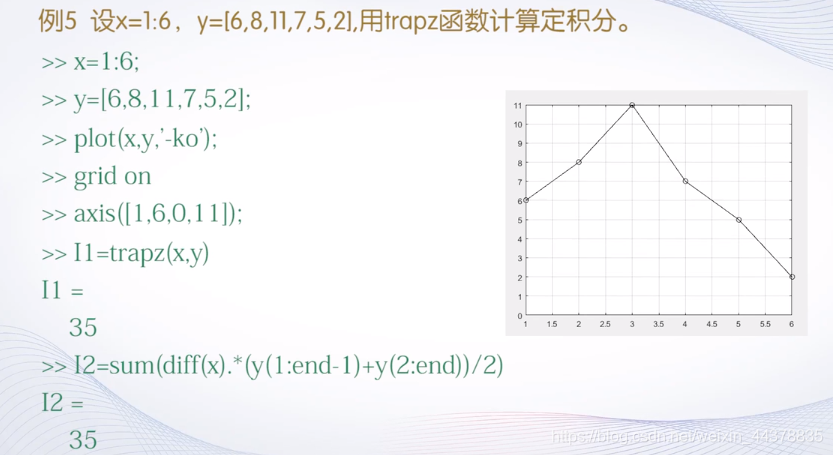
• 基于梯形积分
  

例子：

<3>多重定积分的数值求解

例子：

B 线性方程组求解

B.a 直接法

• 高斯消去法
• 列主元消去法
• 矩阵的三角分解法

<1>利用左除运算符直接解法
Ax=b ====> x=A\b
注意：如果矩阵A是奇异的或者接近奇异的，则MATLAB会给出警告信息。

<2>利用矩阵分解求解线性方程组
1 LU分解
LU分解的基本方法：

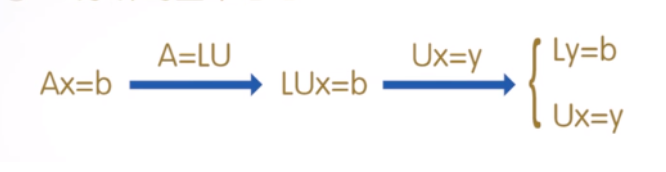
MATLAB的LU分解函数：
[L,U]=lu(A)：产生一个上三角阵U和一个变换形式的下三角阵L，使之满足A=LU。注意，这里的矩阵A必须是方阵。
[L,U,P]=lu(A)：产生一个上三三角阵U和一个下三角阵L以及一个置换矩阵P，使之满足PA=LU。同样，矩阵A必须是方阵。

用LU分解求解线性方程组：

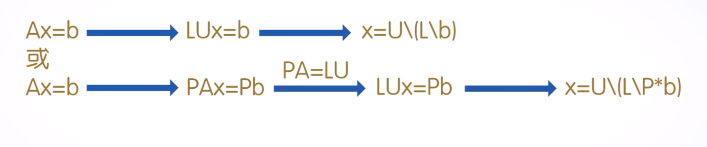
2 QR分解
3 Cholesky分解

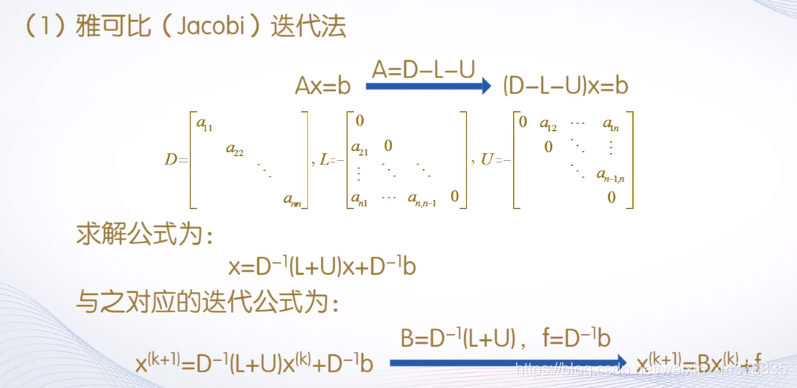
B.b 迭代法

jacobi.m

function [y,n]=jacobi(A,b,x0,ep)D=diag(diag(A)); % 对角阵L=-tril(A,1);U=-triu(A,1);B=D\(L+U);f=D\b;y=B*x0+f;n=1;while norm(y-x0)>=epx0=y;y=B*x0+f;n=n+1;	end

gauseidel.m

function [y,n]=jacobi(A,b,x0,ep)D=diag(diag(A)); % 对角阵L=-tril(A,-1);U=-triu(A,1);B=(D-L)\U;f=(D-L)\b;y=B*x0+f;n=1;while norm(y-x0)>=epx0=y;y=B*x0+f;n=n+1; end

例子：

有时候高斯-赛德尔迭代法求解线性方程组可能不收敛。

C 非线性方程求解与函数极值计算

C.a 非线性方程数值求解

<1>单变量非线性方程求解
函数的调用格式：x=fzero(filename, x0)
其中，filename是待求根方程左端的函数表达式，x0是初始值。

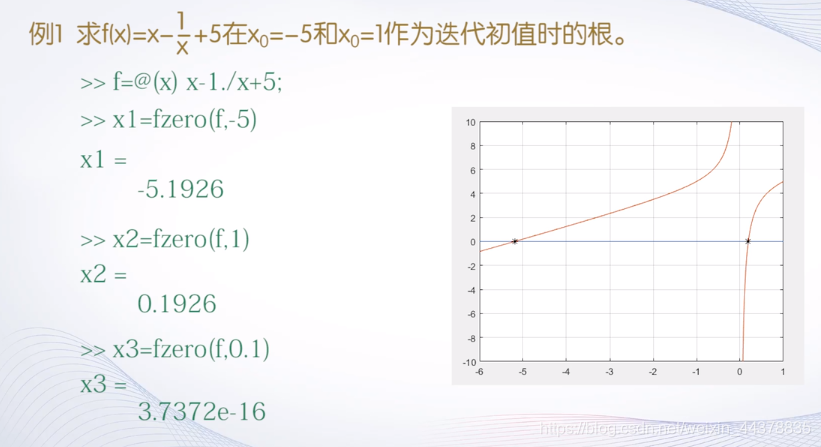
<2>非线性方程组的求解
函数的调用格式为：
x=fsolve(filename, x0, option)
其中，x为返回的近似解，filename是待求根方程左端的函数表达式，x0是初值，option用于设置优化工具箱的优化参数，可以调用optimset函数来完成。

C.b函数极值的计算

• 极大值（最大值）
• 极小值（最小值）

Matlab只考虑最小值问题的计算，如果要求$f(x)$的最大值，可以求$-f(x)$的最小值。
<1>无约束最优化问题
无约束最优化问题的一般描述为：

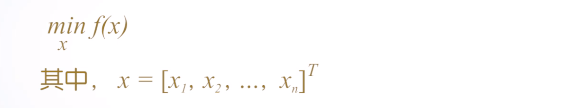
求最小值点和最小值的函数：
[xmin, fmin]=fminbnd(filename, x1, x2, option)
[xmin, fmin]=fminsearch(filename, x0, option)
[xmin, fmin]=fminunc(filename, x0, option)
fminbnd:一元函数
fminsearch:单纯形法。多元
fminunc:拟牛顿法。多元

其中，filename是定义的目标函数。第一个函数的输入变量x1、x2分别表示被研究区间的左右边界。后两个函数的输入变量x0是一个向量，表示极值点的初值。option为优化参数，可以通过optimset函数来设置。

<2>有约束最优化问题
有约束最优化问题的一般描述为：

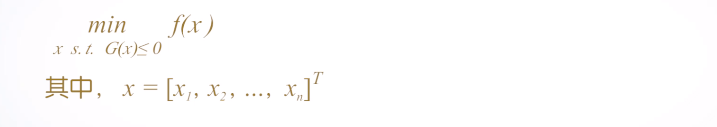
$s.t.是subjectto的缩写，表示x要满足后面的约束条件。$
约束条件可细化为：

• 线性不等式约束
• 线性等式约束
• 非线性不等式约束
• 非线性等式约束
• x的上界和下界

求有约束条件下的最小值的函数为：
[xmin, fmin]=fmincon(filename, x0, A, b, Aeq, beq, Lbnd, Ubnd, Nonf, option)
其中，xmin, fmin,filename,x0和option的含义与求最小值函数相同。其余参数为约束条件，包括线性不等式约束、线性等式约束、x的下界和上界以及定义非线性约束的函数。如果某个约束不存在，则用空矩阵表示。

AX <= b（线性不等式约束，如果是约束是大于，则左右乘-1）
AeqX = beq（线性等式约束）
G(x) <= 0（非线性不等式约束）
Ceq(X) = 0（非线性等式约束）
Lbnd <= X <= Ubub（变量约束）

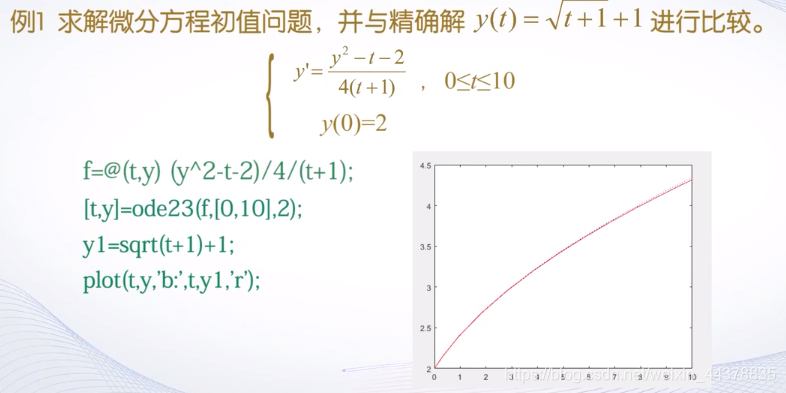
D 常微分方程数值求解

D.a常微分方程数值求解的一般概念

---

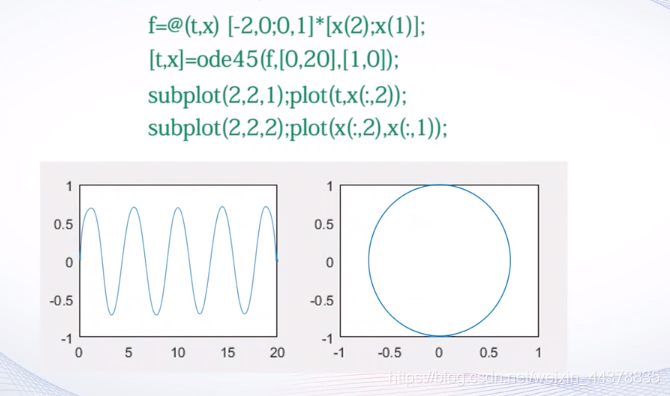
D.b 常微分方程数值求解函数

例子：

例子：

---

D.c 刚性问题

---

图片来源：
https://www.icourse163.org/search.htm?search=%E4%B8%AD%E5%8D%97%E5%A4%A7%E5%AD%A6%20Matlab#/