浦东网站建设公司/阿里指数app下载
EM算法的基本理解
为什么要用EM算法(最大期望算法)?
在机器学习中,我们观察样本,建立模型,然后训练,进行预测。这是一个正常的流程,但是我们想一个问题,现实生活中一定有很多因素使我们无法观测的,也就是隐含数据?怎么办?
算法。。。
如果,只有模型而没有模型参数,那么
1、先猜想隐含数据(算法的
步)。
2、接着基于观察数据和猜测的隐含数据一起来极大化对数似然,求解我们的模型参数(算法的
步)。
由于我们之前的隐藏数据是猜测的,所以此时得到的模型参数一般还不是我们想要的结果。不过没关系,我们基于当前得到的模型参数,继续猜测隐含数据(算法的
步),然后继续极大化对数似然,求解我们的模型参数(
算法的
步)。以此类推,不断的迭代下去,直到模型分布参数基本无变化,算法收敛,找到合适的模型参数。
要学习算法(最大期望算法),首先要了解的是极大似然估计。。。
1、极大似然估计


总的来说:极大似然估计就是用来估计模型参数的统计学方法。
举个例子:
给定一组样本,并且他是高斯模型,怎么确定参数 和
?

高斯分布的概率密度函数: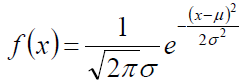
根据上面 MLE 得出的![]()
代入每一个 的高斯概率结果得到
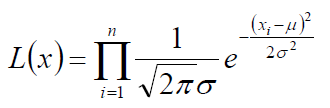
通过取 log 对数对上式进行化简:
这时候我们得到目标函数: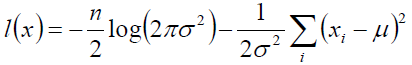
下面就是考虑如何调整 和
来使得目标函数最大。

与我们高斯模型矩估计结果一致。
那么,现在引入我们的话题,随机变量无法直接(完全)观察到,怎么办?
例如:
高斯混合模型GMM
首先还是根据极大似然估计的理论建立目标函数: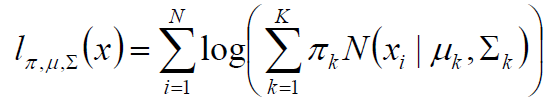
相当于每一个高斯模型的权重,总的
到最后最大是
。



也就是 决定每个高斯模型的重要性。
EM算法

取对数似然函数

这时候引入 Jensen 不等式:
由于对数函数是凹函数,所以有:

 为了寻找最大的下界,那么我们使上式中的等号成立:
为了寻找最大的下界,那么我们使上式中的等号成立: (1)
(1)
进一步,由于 是一种分布的概率,所以加和为
:
![]() (2)
(2)
由上式(1)和(2)得到: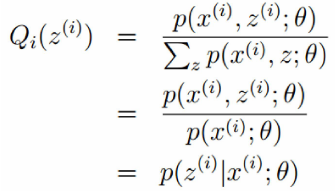
所以,推到算法的过程:

如果 ,那么
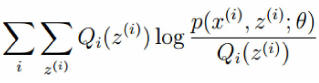 就是我们隐藏数据对数似然的下界,那么就要极大化这个似然函数。
就是我们隐藏数据对数似然的下界,那么就要极大化这个似然函数。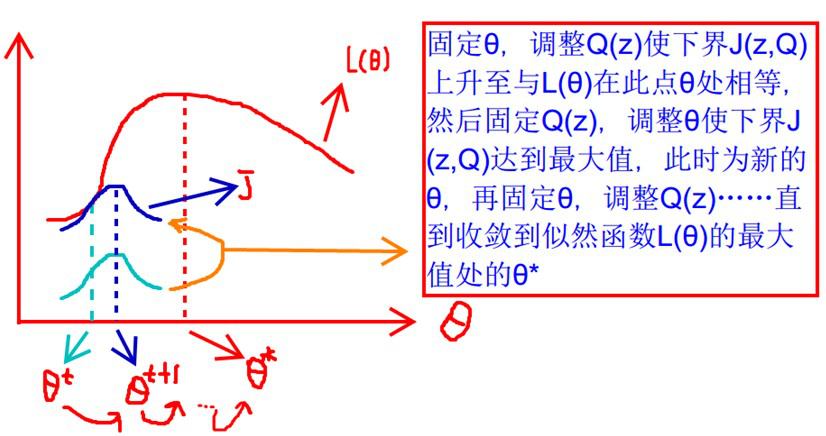
在固定参数 后,使下界拉升的
的计算公式,解决了
如何选择的问题。这一步就是
步,建立 C 的下界。接下来的
步,就是在给定
后,调整
,去极大化 V 的下界
。
所以:
初始化分布参数 ; 重复以下步骤直到收敛:
1、 步骤:根据参数初始值或上一次迭代的模型参数来计算出隐性变量的后验概率,其实就是隐性变量的期望。作为隐藏变量的现估计值:
![]()
2、 步骤:将似然函数最大化以获得新的参数值:
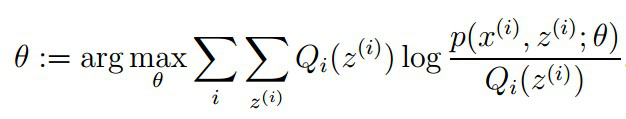
EM的算法流程:
现在我们总结下算法的流程。
输入:观察数据 ,联合分布
, 条件分布
, 最大迭代次数
。
1) 随机初始化模型参数 的初值
。
2) for j from 1 to 开始
算法迭代:
a) 步:计算联合分布的条件概率期望:
b) 步:极大化
,得到
:
c) 如果 已收敛,则算法结束。否则继续回到步骤 a) 进行
步迭代。
输出:模型参数 。
最后,推导高斯混合模型
问题:
步骤:
1、步:
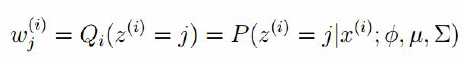
2、步:
把多项分布和高斯分布的参数代入:
3、对均值求偏导:
4、高斯分布均值:
令上式等于 0,解的均值为
5、高斯分布的方差
求偏导,等于 0 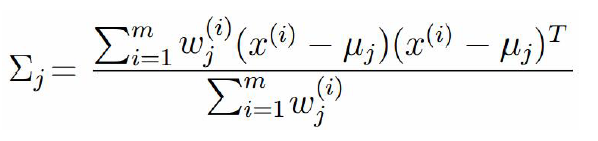
6、多项分布的参数
考察M-step的目标函数,对于 ,删除常数项
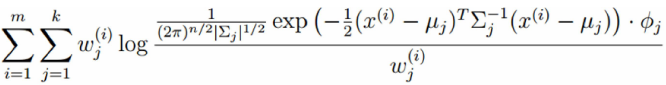
得到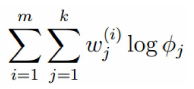
7、拉格朗日乘子法
由于多项分布的概率和为 ,建立拉格朗日方程

注: 这样求解的 一定非负,所以,不用考虑
这个条件
8、求偏导等于 0
总结:
对于所有的数据点,可以看作组份 生成了这些点。组份
是一个标准的高斯分布,利用上面的结论:
![]()


