网站开发宣传标语/百度官方网平台
实验四:矩阵算法
一、实验目的
问题描述:N个人分配N项任务,一个人只能分配一项任务,一项任务只能分配给一个人,将一项任务分配给一个人是需要支付报酬,如何分配任务,保证支付的报酬总数最小。假设N=5,每个人工作和报酬之间的关系如下表所示,求解该问题的最优解
表1.1 任务分配
work1work2work3work4work5
person19075 75 80 60
person23585 556548
person31259590105100
person4451109510598
person57664578890
二、实验要求
(1)做好实验预习
(2)独立完成实验
(3)撰写实验报告
三、实验题目
本实验由于要求较少,只是寻求最优解,因此采用简单的方法。
四、实验环境
本文的编程环境为Ubantu16.04。
本文的编程语言为Python3.7。
五、实验分析与设计思路
本实验采用的是矩阵的方式进行计算,但是其中包含了列表的计算方法,矩阵的相乘。
主要采用的程序:
np.array([])生成一个想要的数组 包括列向量,和行向量。
b=numpy.array([b]).T 行向量转成列向量。
a.dot(b) 向量的乘法。
a*b只是对应相乘不是矩阵的乘法。
a[[1,2],:]=a[[2,1],:] 矩阵的一二两行对调。
左乘单位行向量再乘以已知矩阵再乘以变换矩阵再乘以单位列向量。
六,程序源码
#本实验要求计算利润的最小值杠杠简单
#本次实验打算采用矩阵的方式,不懂勿扰
#np.array([])生成一个想要的数组 包括列向量,和行向量
#b=numpy.array([b]).T 行向量转成列向量
#a.dot(b) 向量的乘法
#a*b只是对应相乘不是矩阵的乘法
#a[[1,2],:]=a[[2,1],:] 矩阵的一二两行对调
#左乘单位行向量再乘以已知矩阵再乘以变换矩阵再乘以单位列向量
#========================================================================
#智能优化算法---计算工作分配方案(原创)
#作者:Vince
#版本号:1.0
#创作日期:2018.10.31
#如需转载,请电联.
#耗时:4h
#=========================================================================
import random
import math
import numpy as np
import copy
import numpy as np
import matplotlib.pyplot as plt
class Min(object):
def __init__(self,newList = [],n=5):
self.newList = newList #初始列表工作的选择
self.diag = np.identity(5) #生成一个五维单位矩阵
self.dhxl = np.array([1,1,1,1,1]) #单位行向量
self.dlxl = np.array([[1],[1],[1],[1],[1]])#单位列向量
self.value = 0#每一次的报酬
self.bestvalue = 100000 #每一次初始种群的最佳报酬
self.bestchoice = np.identity(5) #每一次的初始种群的最佳方案
self.empty = [[-1,-1]] #禁忌表
self.n=n #人数或工作的量
self.num = (((self.n-1)+1)*4/2) #计算循环次数
self.bestdiag=np.identity(5)
def Pso(self):
self.empty = [[-1,-1]]
self.diag = self.bestdiag
self.value = self.bestvalue
i = 0
while i < 10:
index1 = random.randint(0,4) #生成初始种群需要互换的两行
index2 = random.randint(0,4)
if (index1,index2)!=self.empty[-1] and (index2,index1)!=self.empty[-1] and index1!=index2:#比对禁忌表中是否存在
self.empty.append((index1,index2))#将互换两行的行号放入禁忌表
self.diag[[index1,index2],:] = self.diag[[index2,index1],:]#将两行互换
self.value = self.Cul(self.diag)#计算报酬
if self.value < self.bestvalue:#
self.bestvalue = self.value
self.bestdiag = self.diag
self.bestchoice = self.newList*self.bestdiag
i += 1
# print(self.empty)
def Cul(self,diag):
diag = self.newList*diag
diag = self.dhxl.dot(diag)
value = diag.dot(self.dlxl)
return value
def getValue(self):#返回局部最佳值
return self.bestvalue
def getchoice(self):#返回局部最佳方案
return self.bestchoice
def main(turn):
newList = np.array([[90,75,75,80,60],[35,85,55,65,48],[125,95,90,105,100],[45,110,95,105,98],[76,64,57,88,90]])
num = 5
tbv = []
tbc = []
i=0
min = Min(newList,num)
while i
min.Pso()
value = min.getValue()
tbv.append(value)
choice = min.getchoice()
tbc.append(choice)
print('这是第%d次选择'%(i+1))
print('报酬的最小值:%d'%value)
print('最佳选择为:')
print(str(choice))
i += 1
# print('\n')
nb=copy.deepcopy(tbv)
nb.sort() #将所有的局部最佳值进行排序
i = 0
while i
if tbv[i][0] == nb[0][0]:
break
i += 1
print('全局报酬最优解:%d'%tbv[i])
print('最佳选择为:')
print(str(tbc[i]))
return tbv[i][0]
# main(10)
def psoPlot():
x = []
y = []
i=1
while i< 50:
tc = main(i)
#x轴 y轴
x.append(i)
y.append(tc)
print(i)
i += 1
#创建绘图对象,figsize参数可以指定绘图对象的宽度和高度,单位为英寸,一英寸=80px
plt.figure(figsize=(8,8))
#在当前绘图对象进行绘图(两个参数是x,y轴的数据)
plt.plot(x, y, linewidth = '1', label = "test",color='#054E9F', linestyle=':', marker='|')
plt.xlabel("time(s)") #X轴标签
plt.ylabel("value(m)") #Y轴标签
plt.title("A simple plot") #标题
#保存图象
# plt.savefig("easyplot.png")
plt.legend()
plt.show()
psoPlot()
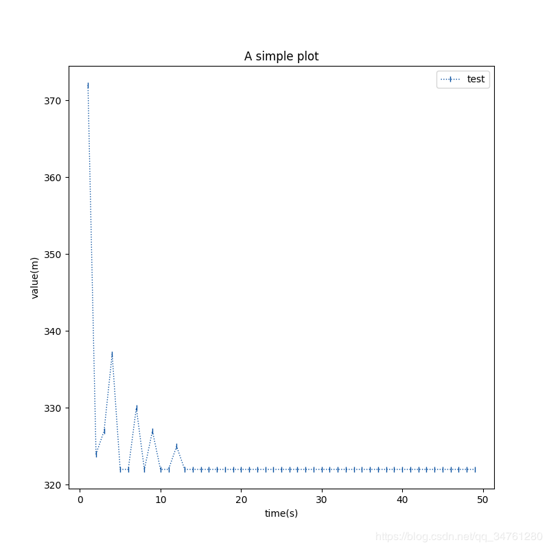
七,运行结果
八,程序原图