请说明如何维护一个支持操作MIN-GAP的动态数据集Q，使得该操作能够给出Q中两个数之间的最小差幅。例如，Q={1，5，9，15，18，22}，则MIN-GAP(Q)返回18-15=3,因为15和18是其中最近的两个数。使用操作INSERT，DELETE，SEARCH和MIN-GAP尽可能高效，并分析它们的运行时间。

题目中的Q是一个有序序列，但输入序列P不一定是有序的。
由于以RED-BLACK-TREE作为基础数据结构，所以INSERT、DELETE、SEARCH的过程及运行时间不再赘述。
仅说明如何计算MIN-GAP以及INSERT和DELETE对MIN-GAP带来的影响。

直接跳至“五、算法过程”

一、常规方法

对于求最小、最大这样的问题，通常就会想到类似贪心的解法。
初始状态时，MIN_GAP肯定时正无穷（+OO）
每加入一个元素，只有元素与前面的值（前驱）的差、与后面的值（后继）的差会影响到MIN_GAP。
算法如下：

def cal_min_gap(P):MIN_GAP = +OOfor num in P:new_gap = INSERT(num)MIN_GAP = min(MIN_GAP, new_gap)return MIN_GAPdef INSERT(num):n = insert num into Qreturn cal_node_gap(n)def DELETE(n):delete n from QMIN_GAP = +OOfor node in Q:node_gap = cal_node_gap(node)MIN_GAP = min(MIN_GAP, node_gap)return MIN_GAPdef cal_node_gap(n):pre = PREDECESSOR(n)suc = SUCCESSOR(n)return min(n.data - pre, suc - n.data)

这种情况下，INSERT的运行时间为O(lgn)，因为加入新元素时可以直接使用前面的计算结果。
但DELETE会受到影响，导致前面的计算结果失效，要全部重新计算，运行时间为O(n)。

二、方法改进一

常规方法中仅额外存储了当前状态下的MIN_GAP，删除结点时导致“当前状态下的MIN_GAP”这个额外信息无效，所以不得不重新计算。
对应的改进方法是把中间过程信息分散到每个结点中，每个结点存储一部分中间信息。
好处是增、删结点后，有一部分计算过的数据还可以直接使用，减少计算量。
缺点是增、删结点后，有一部分计算过的数据失效，需要额外的维护工作量。

在这个题目，在每个结点中额外存储一个数据，即PRE_MIN_GAP，它代表了动态集Q中小于或等于当前结点的所有结点的min gap。
例如，Q={1，5，9，15，18，22}，data为15的结点的PRE_MIN_GAP为Q2={1，5，9，15， 18}的MIN_GAP。

伪代码如下：

def cal_min_gap(P):for num in P:MIN_GAP = INSERT(num)return MIN_GAPdef INSERT(num):n = insert num into Qpre = PREDECESSOR(n)return cal_from_node(n)def DELETE(n):pre = PREDECESSOR(n)delete n from Qreturn cal_from_node(pre)def cal_node_gap(n):pre = PREDECESSOR(n)suc = SUCCESSOR(n)return min(n.data - pre, suc - n.data)def cal_from_node(n):while  n != NULL:new_gap = cal_node_gap(n)n.PRE_MIN_GAP = min(new_gap, PREDECESSOR(n).PRE_MIN_GAP)min_gap = n.PRE_MIN_GAPn = SUCCESSOR(n)return min_gap

在这一算法中，每个node都额外存储了一个可以作为中间计算结果的数据。增、删一个结点时，位于结点前的node，其中间结果可以继续使用，位于node之后的结点的数据则需要更新。
增、删一个结点的时间是相同的，取决于结点的位置，最少为O(lgn)，最多为O(n)

三、方法改进二

上文将中间计算结果分配到每个结点中，使用得当结点改变时，不需要全部重新计算，可以利用部分已经计算的结果，从而节省时间。
但它引入了一个新的问题，就是结点改变时的维护工作过多，导致得不偿失。
因此这次的改进思想是，压缩更新路径。压缩路径的最常见思考方向就是线性结构->树结构。
当前的更新路径是正好线性的，如图所示：

当一个结点p改变了，对于它后面的每一个节点q来说，q的gap1或gap2都 改变了，所以每一个q都要重新计算。
到目前为止，还没有把本文的基础数据结构（红黑树）用上。
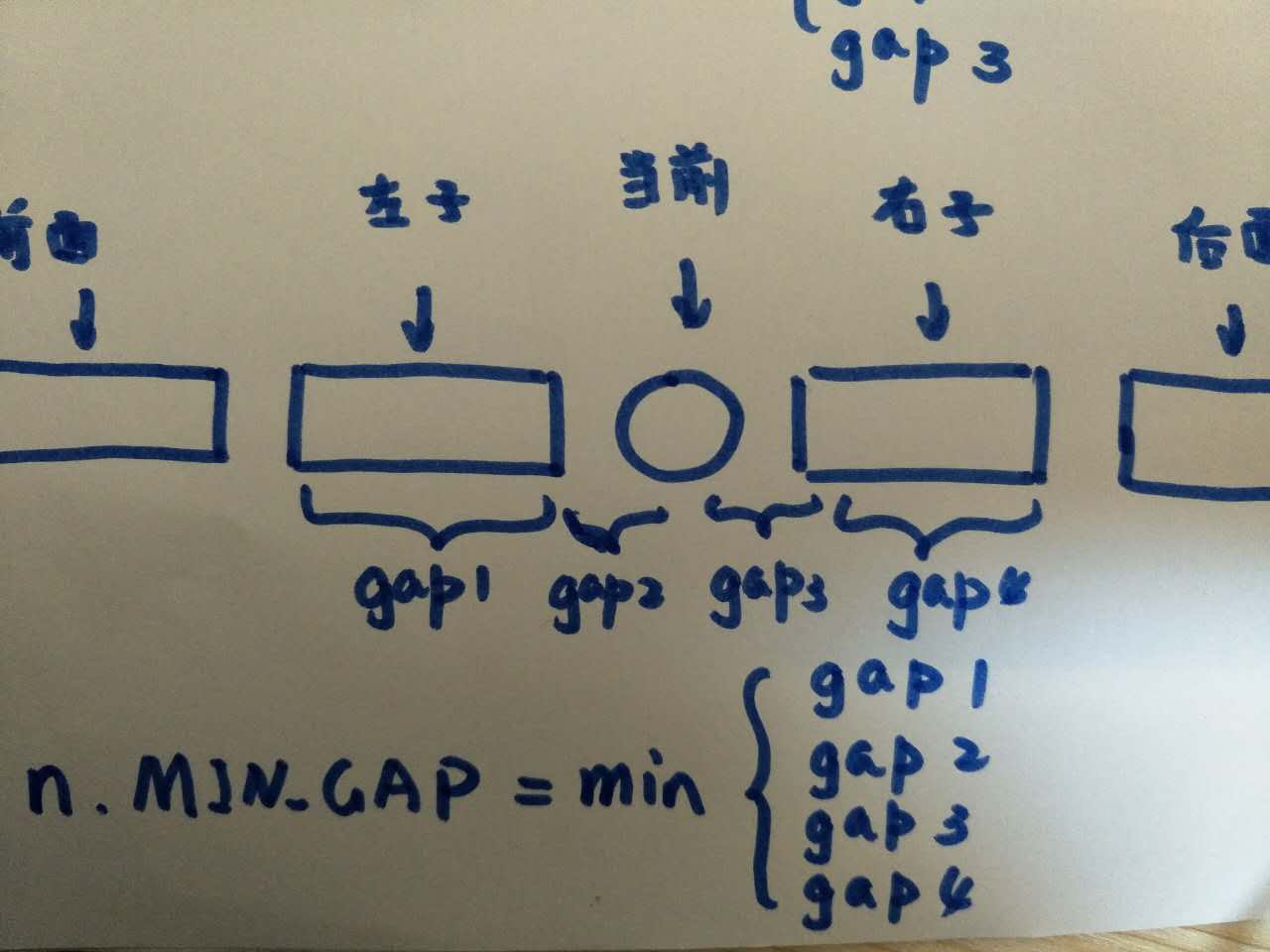
从树的角度来思考，可以是这样的：

由图可知，只有当结点p位于结点q的子树上时，p的改变对会对q造成影响。反过来说，当结点p改变时，只会影响到在这个结点路径上的祖先结点。
从root到任意一个结点所经过的结点数不超过lgn，那么增删一个结点所需花费的维护代价为O(lgn)。

四、算法过程

• 步骤1：基础数据结构
  红黑树，数组中的数值分别作为每个结点的关键字
• 步骤2：附加信息
  min-gap[x]：记录以x为根结点的树的min-gap。当x为叶子结点时，min-gap[x]=0x7fffffff
  min-val[x]：记录以x为根结点的树中最小的关键字
  max-val[x]：记录以x为根结点的树中最大的关键字
• 步骤3：对信息的维护
  在插入的删除的同时，对这三个附加信息进行更新操作，时间复杂度不改变
  
• 步骤4：设计新的操作
  Min_Gap()：返回根结点的min-gap值

五、代码

产品代码

六、测试