上海市建设合同信息表网站/免费发帖的平台有哪些

参考论文 《The Variational Approximation for Bayesian Inference》

令观测值为$\mathrm{x}$，代估参数值为 $\theta$， EM算法所想要最大化的目标函数，最大似然函数可写为：

$$\ln p(\mathbf{x};\mathbf{\theta })=F(q,\mathbf{\theta })+KL(q\Vert p)\text{\hspace{1em}(1)}$$

• $p(\mathrm{x};\mathbf{\theta })$强调$\mathbf{\theta }$是一个参数，例如似然函数便是以之为变量的函数。另一方面，$p(\mathbf{x}\mid \mathbf{\theta })$则强调$\mathbf{\theta }$是一个随机变量。
• $F(q,\mathbf{\theta })=\int q(\mathbf{z})\ln \left(\frac{p(\mathbf{x},\mathbf{z};\mathbf{\theta })}{q(\mathbf{z})}\right)d\mathbf{z}$， $\mathrm{K}\mathrm{L}(q\Vert p)=-\int q(\mathrm{z})\ln \left(\frac{p(\mathrm{z}\mid \mathrm{x};\mathbf{\theta })}{q(\mathrm{z})}\right)d\mathrm{z}$. 因此(1)式的成立就简单地遵循了$p(A)=p(A,B)-p(B|A)$这一条件概率规则。其中，KL也就是著名的KL散度 ($q(z)$与$p(\mathrm{z}\mid \mathrm{x};\mathbf{\theta })$之间)。
• 此处，$\mathbf{z}$是所谓的隐变量，也可以理解为用于求解最大似然问题的人工辅助变量。$q(\mathbf{z})$是任意的概率密度函数。 对于EM算法，$\mathbf{z}$和$q(\mathbf{z})$往往有对应的物理意义。但这里我们并不care，只从纯数学的角度理解。

关于KL散度的介绍推介看这篇 传送门，其中，通过Jensen’s不等式可以证明KL散度非负，即$\mathrm{K}\mathrm{L}(q\Vert p)\ge 0$，因此：
$$\ln p(\mathbf{x};\mathbf{\theta })\ge F(q,\mathbf{\theta })\text{\hspace{1em}(2)}$$
也就是说，(2)找到了最大似然函数的一个下界。因此，以EM算法为代表的许多贝叶斯推断都是在最大化该下界， 也即 $F(q,\mathbf{\theta })$。

具体而言， EM算法是一个两步法对下界$F(q,\mathbf{\theta })$最大化， 从而最大化似然函数：

• E-step:首先将$\mathbf{\theta }$固定为${\mathbf{\theta }}^{\mathrm{O}\mathrm{L}\mathrm{D}}$，优化$q$来最大化$F(q,\mathbf{\theta })$。注意到，给定$\mathbf{\theta }$时$\ln p(\mathbf{x};\mathbf{\theta })$就确定了，因此根据(1)， 最大化$F(q,\mathbf{\theta })$等价于最小化$KL(q\Vert p)$， 而厚泽非负。 当且仅当$q(\mathbf{z})=p\left(\mathbf{z}\mid \mathbf{x};{\mathbf{\theta }}^{\mathrm{O}\mathrm{L}\mathrm{D}}\right)$，取到最小值$0$。此时，$F(q,{\mathbf{\theta }}^{\mathrm{O}\mathrm{L}\mathrm{D}})$ = $\ln p(\mathbf{x};{\mathbf{\theta }}^{\mathrm{O}\mathrm{L}\mathrm{D}})$为最大值。
• M-step: 将$q$固定， 优化$\mathbf{\theta }$来最大化$F(q,\mathbf{\theta })$。假定得到的最优解为${\mathbf{\theta }}^{\mathrm{N}\mathrm{E}\mathrm{W}}$，那么对于固定的$q$，显然KL散度不再为$0$。也就是说，${\mathbf{\theta }}^{\mathrm{N}\mathrm{E}\mathrm{W}}$不仅最大化了$F(q,\mathbf{\theta })$，也让我们的目标$\ln p(\mathbf{x};\mathbf{\theta })$得到了更大的提升。 注意到，由于在E-step中有$q(\mathbf{z})=p\left(\mathbf{z}\mid \mathbf{x};{\mathbf{\theta }}^{\mathrm{O}\mathrm{L}\mathrm{D}}\right)$， 因此在M-step中的优化为：
  $$\begin{array}{rl}F(q,\mathbf{\theta })=& \int p\left(\mathbf{z}\mid \mathbf{x};{\mathbf{\theta }}^{\mathrm{O}\mathrm{L}\mathrm{D}}\right)\ln p(\mathbf{x},\mathbf{z};\mathbf{\theta })d\mathbf{z}\\ & -\int p\left(\mathbf{z}\mid \mathbf{x};{\mathbf{\theta }}^{\mathrm{O}\mathrm{L}\mathrm{D}}\right)\ln p\left(\mathbf{z}\mid \mathbf{x};{\mathbf{\theta }}^{\mathrm{O}\mathrm{L}\mathrm{D}}\right)d\mathbf{z}\end{array}$$
  而后一项是与$\mathbf{\theta }$无关的常数项。 因此记：
  $$Q\left(\mathbf{\theta },{\mathbf{\theta }}^{\mathrm{O}\mathrm{L}\mathrm{D}}\right)=\int p\left(\mathbf{z}\mid \mathbf{x};{\mathbf{\theta }}^{\mathrm{O}\mathrm{L}\mathrm{D}}\right)\ln p(\mathbf{x},\mathbf{z};\mathbf{\theta })d\mathbf{z}$$

EM算法就可以被总结为：

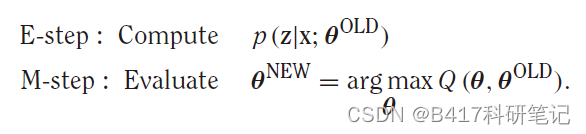
推荐大家可以看下两个实例，再结合数学公式深入理解EM算法。 https://zhuanlan.zhihu.com/p/36331115
我个人觉得一个最好的例子就是K-means算法。 E步骤相当于给定质心的情况下，对数据进行聚类。M步骤相当于分类结束的情况下，根据每类的数据对质心进行更新。 隐函数$z$就代表类别，变量$\mathbf{\theta }$包括了每类的质心参数。

EM算法的核心在于， 原始的最大似然算法需求$p(\mathrm{x};\mathbf{\theta })$的信息， 而EM算法中需求的是$p(\mathbf{z}\mid \mathbf{x};\mathbf{\theta })$的信息，后者在许多时候可能比前者容易获得。但在一些场景中却并不如此，也导致无法使用EM算法。此时， 变分贝叶斯方法是一种更好的算法。