【gmoj】【欧拉函数】Gcd会不会

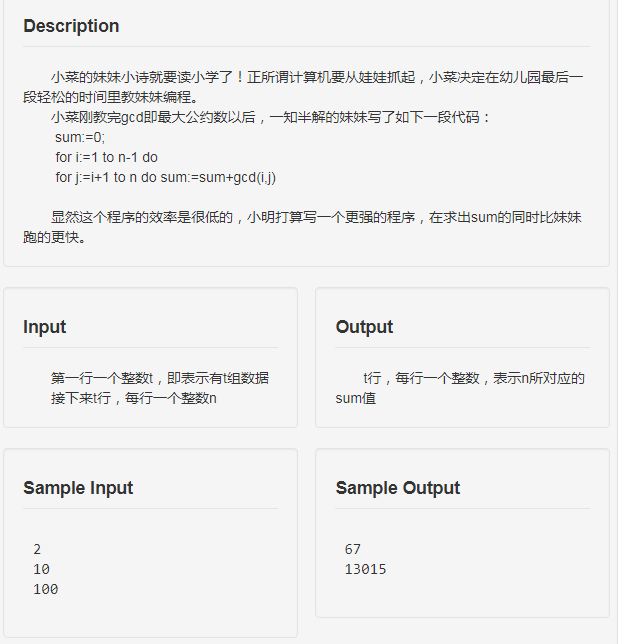
题目

解题思路

题目十分简单直白
就是求1~n内每个数与其他数的最大公因数的和
假设一个d能被 i 整除那么它的贡献如下

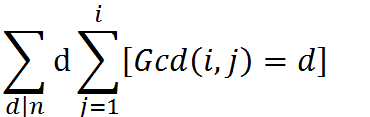
接着将 j/d 那么最大公因数也会 /d，贡献变成这样

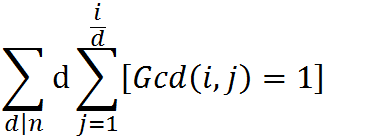
然后我们想到欧拉函数
φ（i）意为1~i中有多少个数与 i 互质
那么式子就可以化为

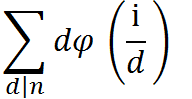
为了节省时间我们可以预处理出所有的φ
可用线性筛o(n)求
不懂的小朋友戳这里
接着我们就枚举 i (所求值/因子) j (因子) ij 即为所求值
转移式即为 ans[ij]=phi[i]*j
最后用前缀和统计答案就好啦

代码

#include<iostream>
#include<cstring>
#include<cstdio>
#define max(a,b) (((a)>(b))?(a):(b))
using namespace std;
long long w,n,t,a[200100],p[1000100],prm[1000100],f[1000100],ans[100010];
int main()
{scanf("%lld",&w);for (int i=1;i<=w;i++){scanf("%lld",&a[i]);n=max(a[i],n); }f[1]=1;memset(p,0,sizeof(p));for (int i=2;i<=n;i++){ if (!p[i]) {f[i]=i-1; prm[++t]=i;}for (int j=1;j<=t&&i*prm[j]<=n;j++){p[i*prm[j]]=1;if (i%prm[j]==0){f[i*prm[j]]=f[i]*prm[j];break;} else f[i*prm[j]]=f[i]*(prm[j]-1);}}for (int i=2;i<=n;i++)for (int j=1;j<=n/i;j++)ans[i*j]+=f[i]*j;for (int i=2;i<=n;i++)ans[i]+=ans[i-1];  for (int i=1;i<=w;i++)printf("%lld %lld\n",ans[a[i]],a[i]);return 0;
}