做网站用windows还是linux/网络推广公司十大排名

在我们做研究的的时候会用到很多群智能算法用于寻优，比如遗传算法、鱼群算法、粒子群算法、还有咱们今天要讲的蚁群算法。将蚁群算法应用于解决寻优问题的基本思路为：用蚂蚁的行走路径表示待优化问题的可行解，整个蚂蚁群体的所有路径构成待优化问题的解空间。路径较短的蚂蚁释放的信息素量较多，随着时间的推进，较短的路径上累积的信息素浓度逐渐增高，选择该路径的蚂蚁个数也愈来愈多。最终，整个蚂蚁会在正反馈的作用下集中到最佳的路径上，此时对应的便是待优化问题的最优解。

蚂蚁找到最短路径要归功于信息素和环境，假设有两条路可从蚁窝通向食物，开始时两条路上的蚂蚁数量差不多，当蚂蚁到达终点之后会立即返回，距离短的路上的蚂蚁往返一次时间短，重复频率快，在单位时间里往返蚂蚁的数目就多，留下的信息素也多，会吸引更多蚂蚁过来，会留下更多信息素。而距离长的路正相反，因此越来越多的蚂蚁聚集到最短路径上来，我们下图可以形象的表示蚁群算法的中心思想。

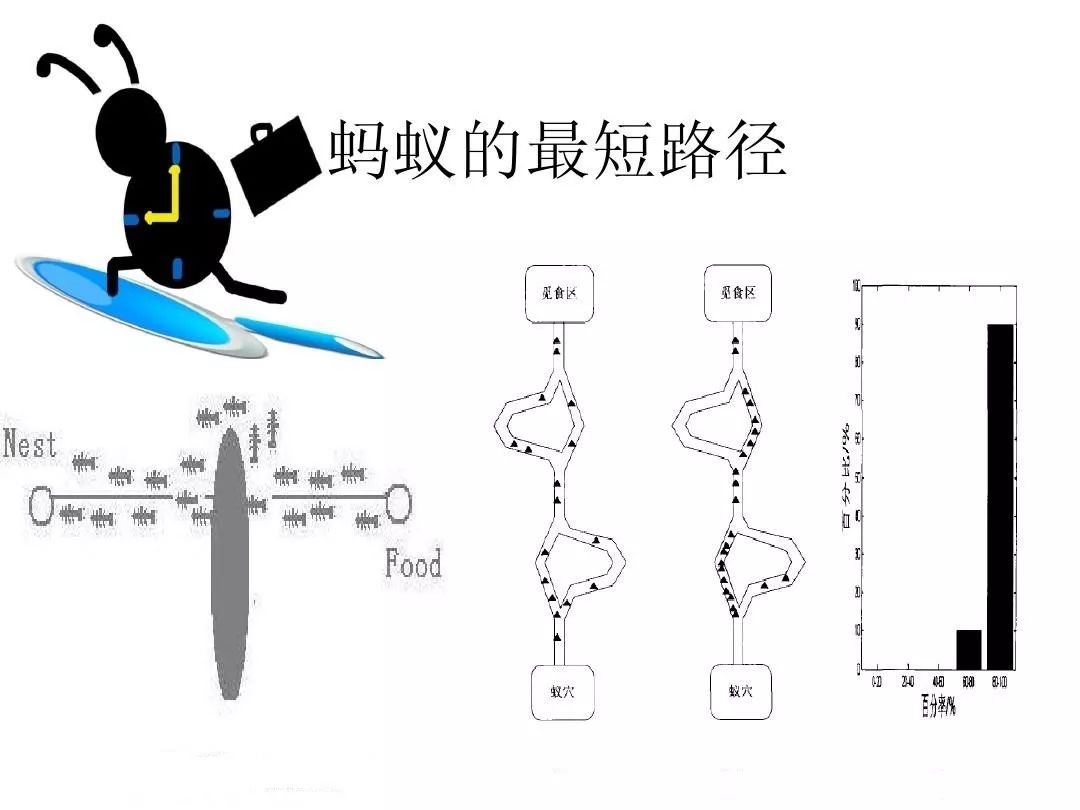
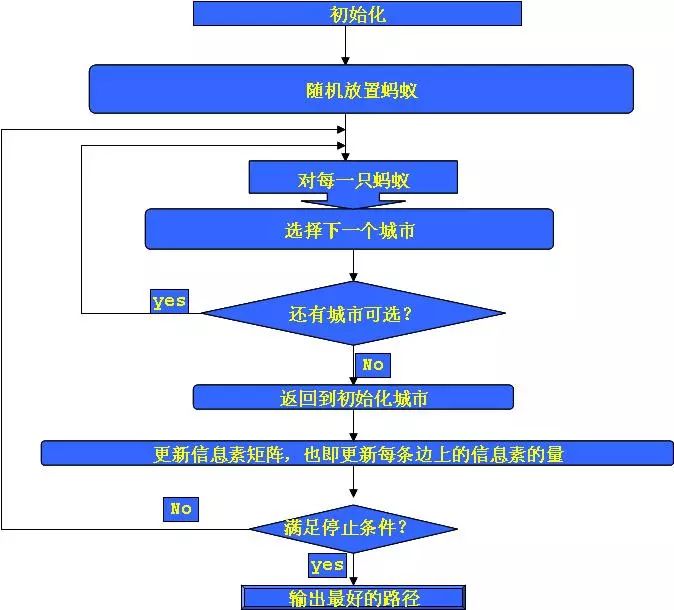
在蚁群算法中，蚂蚁的眼睛观察到的范围是一个方格世界，相关参数为速度半径，一般为3，可观察和移动的范围为3x3方格。蚂蚁在感知范围内寻找食物，如果感知到就会过去，否则朝信息素多的地方走，每只蚂蚁会以很小的可能性犯错，并非都往信息素最多的方向移动。蚂蚁朝信息最多的方向爬行，当周围没有指引时，会按照原来预设的规则行走。而且聪明的蚂蚁会记住最近走过的地方，防止原地转圈。当蚂蚁遇到障碍物时，将按照设定随机选择其行走的方向。当有指引时，将按照觅食规则移动。在刚找到食物或者窝时，蚂蚁散发的信息素最多，当随着走远时，散发的信息素将逐渐减少。在使用蚁群算法进行寻优时，蚁群算法基本工作流程是：

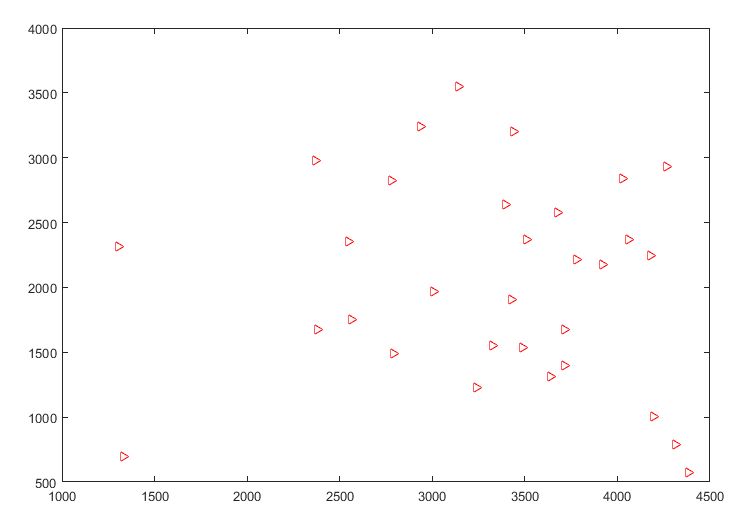
接下来我们举一个实例进行蚁群算法的功能测试，我们做一个城市之间最优旅行方式的计算，为了体现算法强大，我们选择31个城市的坐标，随机选择一个城市作为始发地。我们先看看31个城市的坐标，呈现无规则状态，这为计算增加了不少难度。

在这31所城市中，我们会有31×30×29×28×…×2×1种选择，如果靠人工计算几乎是不可能的事情，就算是计算机也不是一时半刻就可以完成的，但是我们利用鱼群算法，不用挨个计算，可以迅速的找到最合适的旅行路线。我们设置蚂蚁的数量为50个，信息素重要因子为1，启发函数重要因子为5，初次迭代次数为1，最大迭代次数为200。接下来随机产生各个蚂蚁的起点城市，逐个蚂蚁路径选择，逐个城市路径选择，将已访问的城市和没访问的城市以及待访问城市找出来，并采用轮盘赌法选择下一个城市。然后计算各个蚂蚁的路径距离，取出每个蚂蚁的路径，计算最短路径距离和平均距离，更新信息素，逐个蚂蚁计算，逐个城市计算，我们采用MATLAB编程去实现。

通过编辑程序得出运算结果：

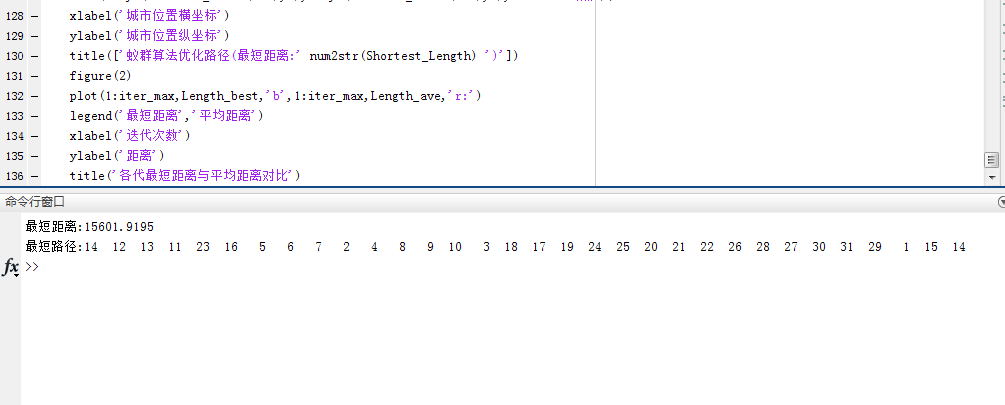
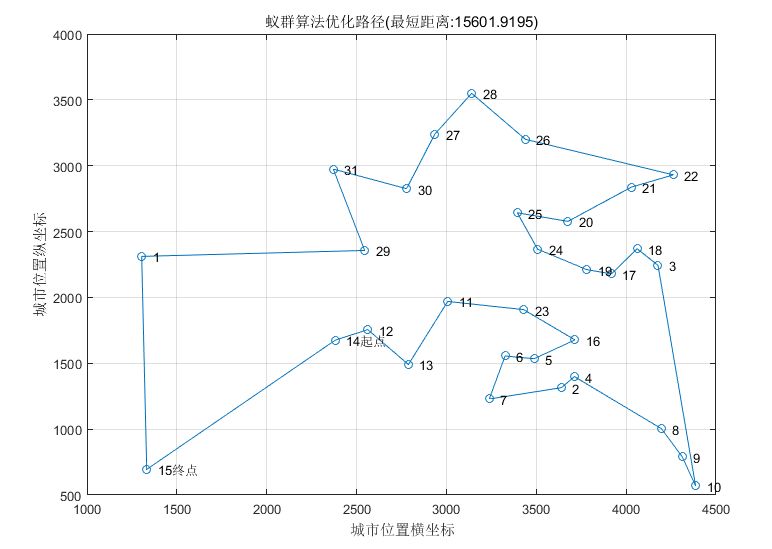
我们可以看出计算出来的最短路径为15601.9195km，随机选择第14个编号作为初始位置：14、12、13、11、23、16、5、6、7、2、4、8、9、10、3、18、17、19、24、25、20、21、22、26、28、27、30、31、29、1、15、14。旅行的路线图如下图所示：

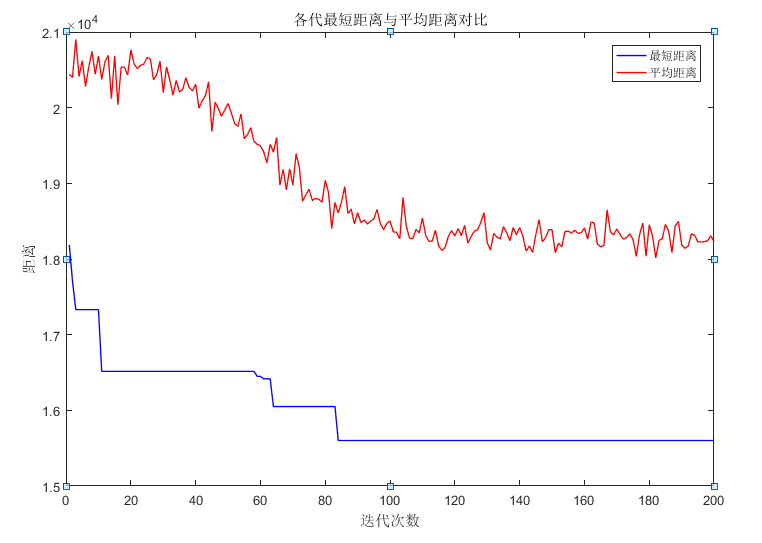
从上面的迭代图可以看出，第一代蚁群计算的距离约为1.8万km，大约经过80代循环之后，基本上找到了最优旅行路线。除了本文的应用，蚁群算法应用广泛，也可以应用于其他组合优化问题，如线性最优解问题、指派问题、Job—shop调度问题、车辆路由问题、图着色问题和网络路由问题等。最近几年，该算法在网络路由中的应用受到越来越多学者的关注，并提出了一些新的基于蚁群算法的路由算法。同传统的路由算法相比较，该算法在网络路由中具有信息分布式性、动态性、随机性和异步性等特点，而这些特点正好能满足网络路由的需要。