西安网站制作公司哪/免费发布友链

= = = = 方法递归调用 = = = =

前言：刚开始学习递归的时候是有一定困难的，光用自己的脑子去想，去无限被套娃真的是非常的痛苦…这一模块拖了好长时间，通过查找一些资料也终于有了自己的一些理解和心得体会。

一、基本介绍
1、简单的说: 递归就是方法自己调用自己,每次调用时传入不同的变量.递归有助于编程者解决复杂问题,同时可以让代码变 得简洁。

二、递归调用机制（举例说明）
以下两个问题都可参考递归的重要规则，只有知道它的规则、原理才能更好的理解它。
1．执行一个方法时，就创建一个新的受保护的独立空间(栈空间)
2.方法的局部变量是独立的，不会相互影响,比如n变量
3．如果方法中使用的是引用类型变量(比如数组，对象)，就会共享该引用类型的数据。
4。递归必须向退出递归的条件逼近，否则就是无限递归,出现
StackOverflowError，死龟了:)
5.当一个方法执行完毕，或者遇到return，就会返回，遵守谁调用，就将结果返回给谁,同时当方法执行完毕或者返回时，该方法也就执行完毕。

例：
①打印问题
打印问题虽然简单，但是初次接触到也很容易搞错，就算没错的也对它的调用执行机制模模糊糊说不上来。

public class Recursion01 {//编写一个 main 方法 public static void main(String[] args) {T t1 = new T();t1.test(4);    //输出什么？ n=2 n=3 n=4 int res = t1.factorial(5);System.out.println("5 的阶乘 res =" + res）} }
class T { public void test(int n) {if (n > 2) {test(n - 1); }System.out.println("n=" + n);}

②阶乘问题

//factorial 阶乘 
public int factorial(int n) {if (n == 1) {return 1; } else { return factorial(n - 1) * n;} }

三、经典例题（斐波拉契、猴子吃桃）
1、请使用递归的方式求出斐波那契数 1,1,2,3,5,8,13…给你一个整数 n，求出它的值是多少
思路分析：
1） 当 n = 1 斐波那契数 是 1
2） 当 n = 2 斐波那契数 是 1
3） 当 n >= 3 斐波那契数 是前两个数的和
4） 这里就是一个递归的思路

class T {
public int fibonacci(int n) {if( n >= 1) {//范围是大于1的数 if( n == 1 || n == 2) {//最开始两个数是1return 1; } else {return fibonacci(n-1) + fibonacci(n-2);//规律，（自己要找） } } else { System.out.println("要求输入的 n>=1 的整数");return -1; }}

2、猴子吃桃子
问题:有一堆桃子，猴子第一天吃了其中的一半，并再多吃了一个，以后每天猴子都吃其中的一半，然后再多吃一个。当到第10天时，想再吃时(即还没吃)，发现只有1个桃子了。问题:最初共多少个桃子?
思路分析：逆推

1. day = 10 时 有 1 个桃子
2. day = 9 时 有 (day10 + 1) * 2 = 4
3. day = 8 时 有 (day9 + 1) * 2 = 10
4. 规律就是 前一天的桃子 = (后一天的桃子 + 1) *2（找出规律就是我们的能力 ）
5. 递归

public class RecursionExercise01 { 
//编写一个 main 方法 public static void main(String[] args) { T t1 = new T(); //桃子问题 int day = 0; int peachNum = t1.peach(day);if(peachNum != -1) { System.out.println("第 " + day + "天有" + peachNum + "个桃子");}public int peach(int day) { if(day == 10) { //第 10 天，只有 1 个桃 return 1; } else if ( day >= 1 && day <=9 ) {return (peach(day + 1) + 1) * 2;//规则，自己要想} else { System.out.println("day 在 1-10"); return -1; } } }

通过上述几个例子可以总结：
1、递归最重要的是要找出把问题不断缩小的等价条件。
2、再就是找出终止递归的条件。

四、递归调用应用实例（迷宫问题、汉诺塔）
1、老鼠出迷宫
从某个起点出发走到终点，白色代表可以走，红色为屏障；根据下面地图设置一个简单迷宫。老鼠得到的路径，和程序员设置的找路策略有关，即：找路的上下左右的顺序相关。

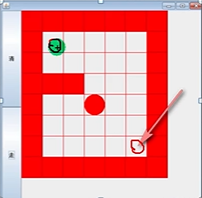
思路分析：
1、使用递归思想解决老鼠出迷宫
2、findWay方法就是专门来找出迷宫的路径
3、map就是二维数组，即表示迷宫
4、i ，j就是老鼠的位置，初始化位置为（1，1）
5、因为我们是递归的找路，所以我先规定map数组的各个值的含义：
0表示可以走 1 表示障碍物 2表示是通路 3表示走过，但是走不通
6、当map[6][5] = 2 就说明找到通路，就可以结束 ，否则就继续找。（目标点在map[6] [5] ）
7、如果找到就返回ture 否则返回false
8、先确定老鼠找路策略 下 -> 右 -> 上 -> 左

public class MiGong{public static void main(String[] args) {//设置迷宫障碍物位置int[][] map = new int[8][7];//8行7列for(int i = 0 ;i < 7;i++){//设置第一行和最后一行map[0][i] = 1;map[7][i] = 1;}for(int j = 0 ;j < 8;j++){//设置第一列和最后一列map[j][0] = 1;map[j][6] = 1;}map[3][1] = 1;//单独设置两道墙map[3][2] = 1;//输出原始数组（地图）for (int i = 0; i < map.length  ; i++ ) {for (int j = 0; j < map[i].length ; j++ ) {System.out.print(map[i][j] + " ");}System.out.println();}T mouse = new T();boolean result = mouse.findWay(map,1,1);//从（1，1）位置出发System.out.println("======结果为：=====");//找路后的地图for (int i = 0; i < map.length  ; i++ ) {for (int j = 0; j < map[i].length ; j++ ) {System.out.print(map[i][j] + " ");}System.out.println();}if(result){//判断是否找到System.out.println("找到了！");}else{System.out.println("没找到！");}}}class T{public boolean findWay(int[][] map , int i , int j){//i,j表示当前位置//i = 1,j = 1;//初始位置为map[1][1]if(map[6][5] == 2){//每次调用方法先看当前位置是否在终点return true; //说明找到了}if(map[i][j] == 0){map[i][j] = 2;//假定这个位置能走通//找路策略为：下 -> 右 -> 上 -> 左if(findWay(map,i+1,j)){//判断向下走是否为通路return true;}else if(findWay(map,i,j+1)){//判断向右走是否为通路return true;}else if(findWay(map,i,j)){//判断向上走是否为通路return true;}else if(findWay(map,i,j-1)){//判断向左走是否为通路return true;}else{//假定此位置为通路不成立map[i][j] = 3;//将它改为走过的但是不通的路}}else{return false;//当前位置不为0return false ;}
}

2、汉诺塔问题

题目：给一个盘子数 Num ，共有三根柱子。所有的盘子在任何时候从上到下都要按照从小到大的顺序，即在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。开始时所有的盘子都放在一个柱子上。问 : 盘子是如何移动的？

思路：如何才能将A塔的盘子全部移动到C塔去？
1、如果只有一个盘子，那么就可以直接说明A->C
== 2、如果有两个盘子呢？那就要先把A 借助C移到B,再把剩下的A塔的盘子移到C，再把B中的盘子移到C，完成。==
3、如果3个、四个、n个呢？？
这里容易想不到的就是它的规律，以及如何定义一个方法，方法的形式参数怎么设计，即怎么实现。这两个问题困扰了我好几天（不想直接看代码，一直反复地理解方法和递归的运用，结果一直想不出来，后面实在写不出来看到代码就醍醐灌顶）终究是代码实现能力以及解决问题的思考能力太欠缺了…得要慢慢加强。
4、先自己在纸上画三个盘子的，四个盘子的。理解了它的过程以后就能发现它的一点规律了。（这里其实用到一种数学思维，整体法，即把上面和下面看成整体，不管它的数量如何）。
5、假设有N个盘子，可以把它看作两部分（因为从2个盘子开始就可以用此规律了）最底下的盘子和其余上面的n-1个盘子。
6、那么我们只要先把n-1个盘子移到B，再把最下面的移到C，再把B的n-1个移到C。
7、那n-1个B塔的盘子怎么移到C呢？再重复第5和第6步…
8、推断到这里很明显就能感觉到用递归来解决此问题了。
9、接下来就是代码实现

public class HanoiTower{public static void main(String[] args){//a, b, c分别表示A塔，B塔,C塔char a = 'A';char b = 'B';char c = 'C';Tower t1 = new Tower();t1.move(5,a,b,c);//5个盘子，A,B,C三塔}
}class Tower{//num表示要移动的个数, a, b, c分别表示A塔，B塔,C塔public void move(int num , char a ,char b ,char c){if(num == 1){//如果只有一个盘System.out.println(a+"->"+c);}else if(num >= 2){//两个及以上盘//如果有多个盘，可以看成两个 , 最下面的和上面的所有盘(num-1)move(num - 1 ,a , c ,b);//把num-1个盘从A塔移到B塔去，但是要借助C塔System.out.println(a+"->"+c);//再把A塔剩下的最大的一个盘移到C塔move(num - 1 ,b , a ,c);//最后把B塔的num-1个盘移到C塔去，完成。return ;}elseSystem.out.println("你输入的个数不对");//盘子数不在大于1的范围里报错return ;}
}

核心代码其实就那么几行，但是当自己敲出来了真的觉得原来代码可以这么美~

这几天看到迷宫和汉诺塔问题心总是静不下来，遇到难点了总是想逃避…最后终于算解决了，最起码是能理解这些代码了。以后还会遇到各种各样的困难，希望都能坚持下去吧！！
学习如此，生活亦是。
我亦无他，唯手熟尔。

以上，共勉。