邻接矩阵

😄

Wilson Huang 2020/8/2

为什么引出邻接矩阵

若图有很多边，则把图表示成变得表或邻接表不便于执行图的算法。

则我们用矩阵来表示图。

两种用矩阵表示图的类型

1. 基于顶点的相邻关系
2. 基于顶点与边的关联关系

具体定义

假设 $G=(V,E)$ 是简单图，其中 $|V|=n$ 。假设把 $G$ 的顶点任意排列成 $v_1,v_2,\cdot \cdot \cdot ,v_n$ 。对这个顶点序列来说， $G$ 的 邻接矩阵$A$ (或 $A_G$) 是一个 $n\times n$ 的 0-1 矩阵，满足的性质：

1. 当 $v_i$ 与 $v_j$ 相邻的时候第 $(i,j)$ 项是 1.
2. 当 $v_i$ 与 $v_j$ 不相邻的时候第 $(i,j)$ 项是 0.

换句话说：若邻接矩阵是 $A=[A_{ij}]$ ，则 $a_{ij}=1$ 当{vi,vj}\{v_i,v_j\}{vi​,vj​}是 $G$ 的一条边，否则为 $0$.

For example

一幅图如下所示

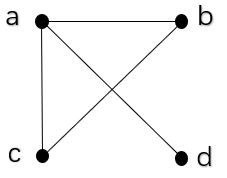
将顶点排列成 $a,b,c,d$ 则表示这个图的矩阵如下
$$\left(\begin{array}{c}a\\ b\\ c\\ d\end{array}\right)=\left(\begin{array}{cccc}0& 1& 1& 1\\ 1& 0& 1& 0\\ 1& 1& 0& 0\\ 1& 0& 0& 0\end{array}\right)$$

tips: a 与 b,c,d 相连，则为[0 1 1 1]，以此类推

• 需要注意的是，图的邻接矩阵依赖于所选择的顶点的顺序。因此带 n 个顶点的图有 n! 个不同的邻接矩阵（n 个顶点有 n! 个不同的邻接顺序）

在简单图中的性质

简单图的邻接矩阵是对称的，即 $a_{ij}=a_{ji}$

• 因为当 $v_i$ 与 $v_j$ 相邻的时候，这两项都是 1，否则为 0.

• 因为简单图无环，所以每一项 $a_{ii}$ 都是 0.

用邻接矩阵来表示带环和多重边的无向图

步骤

1. 把顶点 $a_i$ 上的环表示成邻接矩阵第 $(i,i)$ 位置上的1。
2. 邻接矩阵的第 $(i,j)$ 项等于与 $v_i,v_j$ 关联的边数。

例子

有一幅伪图如下

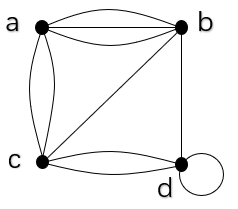
将顶点排列成 $a,b,c,d$ 则表示这个图的矩阵如下
$$\left(\begin{array}{c}a\\ b\\ c\\ d\end{array}\right)=\left(\begin{array}{cccc}0& 3& 0& 2\\ 3& 0& 1& 1\\ 0& 1& 1& 2\\ 2& 1& 2& 0\end{array}\right)$$

性质

• 包括多重图与伪图在内的所有无向图都是具有对称的邻接矩阵

用邻接矩阵来表示有向图

若有向图 $G=(V,E)$ 从 $v_i$ 到 $v_j$ 有边则它的矩阵在 $(i,j)$ 位置上有1，其中 $v_1,v_2,\cdot \cdot \cdot ,v_n$ 是有向图任意的顶点序列。

换句话说若 $A=[a_{ij}]$ 是相对于这个顶点列表的邻接矩阵，则：

$a_{ij}=1$ 若{vi,vj}\{v_i,v_j\}{vi​,vj​} 是 $G$的一条边，否则为 $0$

• 有向图的邻接矩阵不一定是对称的，因为当从 $v_i$ 到 $v_j$ 有边时，反过来可能没有边

如何取舍邻接表和邻接矩阵

1. 一个简单图包含的边相对较少（ 稀疏图 ），邻接表更合适。

   稀疏图的邻接矩阵是稀疏矩阵，即矩阵中只有少量元素不为0

2. 稠密的 简单图，邻接矩阵更合适