建站工作室 网站建设工作室百度网址大全网站大全

引言

• 对于大量的输入数据，链表的线性访问时间太慢，不宜使用。下面将介绍一种简单的数据结构，其大部分操作的运行时间平均为O(log N)。

二叉查找树ADT的性质

• 对于树中的每个节点X，它的左子树中的所有项的值小于X的值，而它的右子树中所有项的值大于X的值。

二叉查找树的结构

private static class BinaryNode<AnyType>
{//Constructors结构BinaryNode(AnyType theElement){this(theElement, null, null);}BinaryNode(AnyType theElement, BinaryNode<AnyType> left, BinaryNode<AnyType> right){this.element = theElement;this.left = left;this.right = right;}AnyType element;	//节点数据BinaryNode<AnyType> left;	//左子树BinaryNode<AnyType> right;	//右子树
}

insert方法

private BinaryNode<AnyType> insert(AnyType x, BinaryNode<AnyType> t){if(t==null){return new BinaryNode<>(x);}int compareReuslt = x.compareTo(t.element);if(compareReuslt<0){t.left = insert(x. t.left);}else if(compareResult>0){t.right = insert(x, t.right);}else{//Duplicate;do nothing元素重复，不用插入}return t;
}

findMin方法和findMax方法（递归与非递归实现）

• findMin的递归实现

private BinaryNode<AnyType> findMin(BinaryNode<AnyType> t){if(t==null){return null;}else if(t.left==null){return t;}return findMin(t.left);
}

• findMax的非递归实现

private BinaryNode<AnyType> findMax(BinaryNode<AnyType> t){if(t!=null){while(t.right != null){t = t.right;}}return t;
}

remove方法

• 正如许多数据结构一样，最困难的操作是remove（删除）。我们需要考虑如下几种情况。
• 节点是一片树叶，可以被立即删除
• 节点有一个儿子，则可以在其父节点调整链，绕过该节点，达到删除目的
• 该节点有两个儿子，用其右子树的最小数据代替该节点的数据，并递归地删除那个节点（让它为空）。因为右子树中最小的节点不可能有左儿子，所以第二次remove要容易一些。

private BinaryNode<AnyType> remove(AnyType x, BinaryNode<AnyType> t){if(t!=null){return t;//Item not found;do nothing}int compareResult = x.compareTo(t.element);if(compareResult<0){t.left = remove(x, t.left);}else if(compareResult>0){t.right = remove(x, t.right);}else if(t.left!=null&&t.right!=null){t.element = findMin(t.right).element;t.right = remove(t.element, t.right);}else{t = (t.left!=null)?t.left:t.right;}return t;
}

• 上述程序完成了删除的工作，但是它的效率并不高，因为他沿该树进行了两趟搜索以查找和删除右子树中最小的节点。
• 如果删除的次数不多，通常使用的策略是懒惰删除；当一个元素要被删除时，让它留在树中，而只是被标记为删除。这特别是在有重复项时很常用，因为此时记录出现频率数的域可以减1。如果树中的实际节点数和“被删除”的节点数相同，那么树的深度预计只上升一个小的常熟（为什么？），因此，存在一个与懒惰删除相关的非常小的时间损耗。再有，如果被删除的项是重新插入的，那么分配一个新的单元的开销就避免了。
  

看一个案例（说明二叉查找树可能的问题）

给定一个数列｛1，2，3，4，5，6｝，要求创建一颗二叉查找树

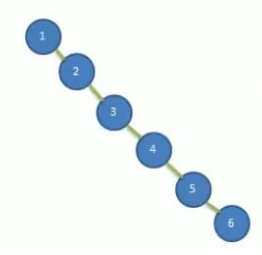
问题分析：

1. 左子树全部为空，形式上看，更像一个单链表
2. 插入速度没有影响
3. 查询速度明显降低（因为需要依次比较），不能发挥二叉查找树的优势，因为每次还需要比较左子树，查询速度比单链表还慢
4. 解决方案-平衡二叉树（AVL）

• 《数据结构与算法分析（Java语言描述）》读后笔记