目录

一.二叉查找树(二叉搜索树，BST)

 1.1查找操作

1.2插入操作

1.3删除操作

1.4支持重复数据的二叉查找树

1.5二叉查找树的性能分析

二.平衡二叉查找树

2.1定义

2.2红黑树

2.3为什么红黑树这么受欢迎

三.哈希表为什么不能替代二叉查找树

四.MySQL数据库索引是如何实现的

基于数组的解决方案

基于哈希的解决方案

基于平衡二叉查找树的解决方案

影响IO效率的因素

B树

磁盘预读知识补充

B树的查找

B+树

---

先来看一下什么是二叉查找树

一.二叉查找树(二叉搜索树，BST)

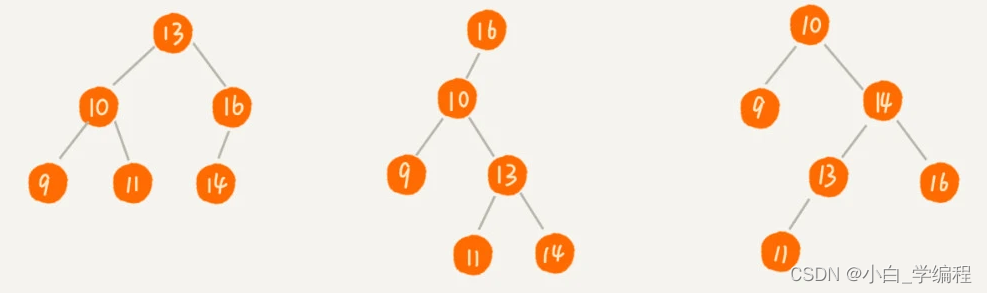
对于二叉查找树中的任意一个节点，其左子树中每个节点的值都要小于这个节点的值，而右子树中每个节点的值都要大于这个节点的值

 1.1查找操作

我们先取根节点，如果它等于我们要查找的数据，那就返回。如果要查找的数据比根节点的值小，那就在左子树中递归查找；如果要查找的数据比根节点的值大，那就在右子树中递归查找。

public class BinarySearchTree {private Node tree;public Node find(int data) {Node p = tree;while (p != null) {if (data < p.data) p = p.left;else if (data > p.data) p = p.right;else return p;}return null;}public static class Node {private int data;private Node left;private Node right;public Node(int data) {this.data = data;}}
}

1.2插入操作

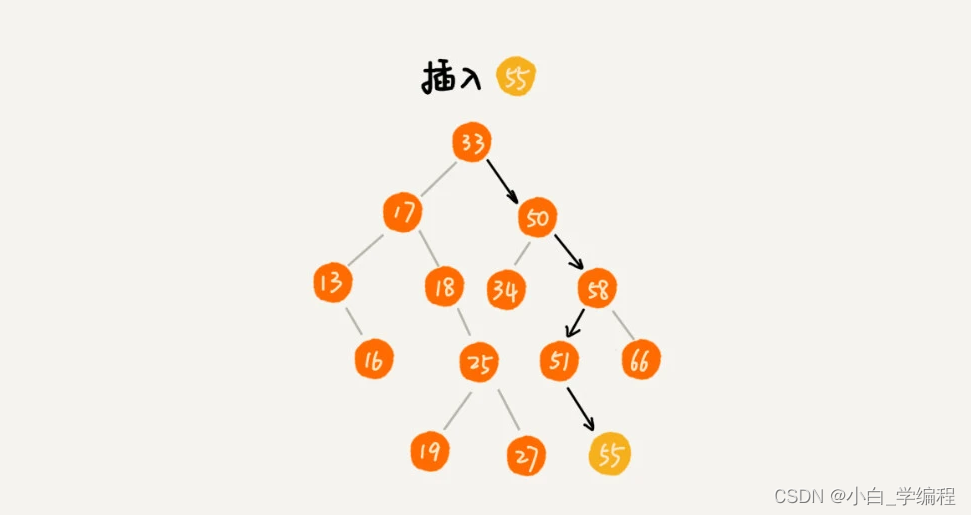
我们从根节点开始，依次比较要插入的数据和节点的大小关系。

• 如果要插入的数据比节点的数据大，并且节点的右子树为空，就将新数据直接插到右子节点的位置；如果不为空，就再递归遍历右子树，查找插入位置。
• 同理，如果要插入的数据比节点数值小，并且节点的左子树为空，就将新数据插入到左子节点的位置；如果不为空，就再递归遍历左子树，查找插入位置。

public void insert(int data) {if (tree == null) {tree = new Node(data);return;}Node p = tree;while (p != null) {if (data > p.data) {if (p.right == null) {p.right = new Node(data);return;}p = p.right;} else { // data < p.dataif (p.left == null) {p.left = new Node(data);return;}p = p.left;}}
}

1.3删除操作

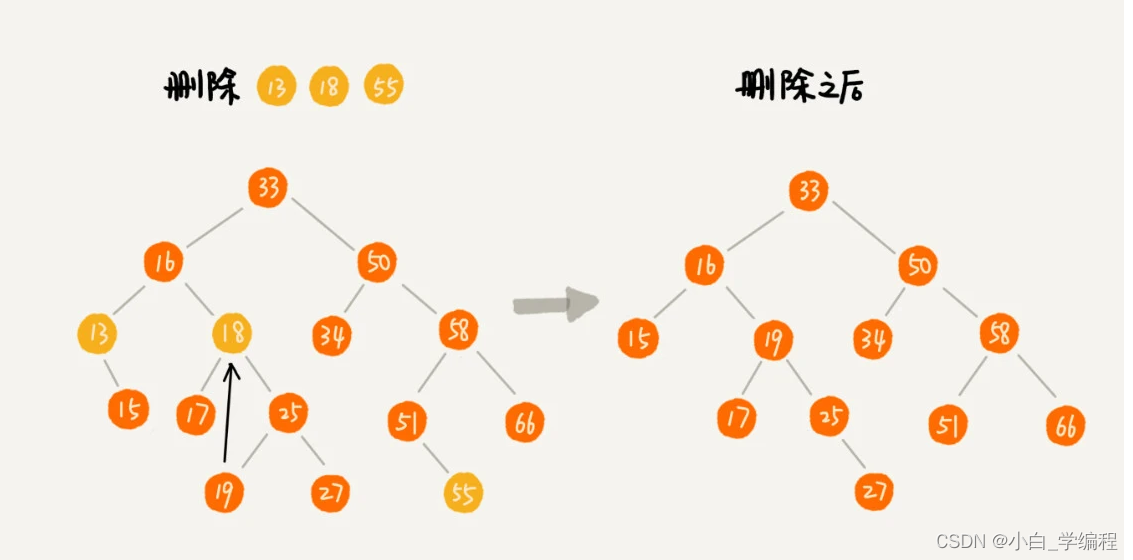
针对要删除节点的子节点个数的不同，我们需要分三种情况来处理。

• 第一种情况是，如果要删除的节点没有子节点，我们只需要直接将父节点中，指向要删除节点的指针置为null。比如图中的删除节点55。
• 第二种情况是，如果要删除的节点只有一个子节点（只有左子节点或者右子节点），我们只需要更新父节点中，指向要删除节点的指针，让它指向要删除节点的子节点就可以了。比如图中的删除节点13。
• 第三种情况是，如果要删除的节点有两个子节点，这就比较复杂了。我们需要找到这个节点的右子树中的最小节点，把它替换到要删除的节点上。然后再删除掉这个最小节点，因为最小节点肯定没有左子节点（如果有左子结点，那就不是最小节点了），所以，我们可以应用上面两条规则来删除这个最小节点。比如图中的删除节点18。

public void delete(int data) {Node p = tree; // p指向要删除的节点，初始化指向根节点Node pp = null; // pp记录的是p的父节点while (p != null && p.data != data) {pp = p;if (data > p.data) p = p.right;else p = p.left;}if (p == null) return; // 没有找到// 要删除的节点有两个子节点if (p.left != null && p.right != null) { // 查找右子树中最小节点Node minP = p.right;Node minPP = p; // minPP表示minP的父节点while (minP.left != null) {minPP = minP;minP = minP.left;}p.data = minP.data; // 将minP的数据替换到p中p = minP; // 下面就变成了删除minP了pp = minPP;}// 删除节点是叶子节点或者仅有一个子节点Node child; // p的子节点if (p.left != null) child = p.left;else if (p.right != null) child = p.right;else child = null;if (pp == null) tree = child; // 删除的是根节点else if (pp.left == p) pp.left = child;else pp.right = child;
}

关于二叉查找树的删除操作，还可以单纯将要删除的节点标记为“已删除”，但是并不真正从树中将这个节点去掉。这样原本删除的节点还需要存储在内存中，比较浪费内存空间，但是删除操作就变得简单了很多。而且，这种处理方法也并没有增加插入、查找操作代码实现的难度。

1.4支持重复数据的二叉查找树

针对包含值相同的节点的二叉查找树，有两种存储方式。

• 第一种方法：二叉查找树中每一个节点不仅会存储一个数据，因此我们通过链表和支持动态扩容的数组等数据结构，把值相同的数据都存储在同一个节点上
• 第二种方法：每个节点仍然只存储一个数据。在查找插入位置的过程中，如果碰到一个节点的值，与要插入数据的值相同，我们就将这个要插入的数据放到这个节点的右子树，也就是说，把这个新插入的数据当作大于这个节点的值来处理。

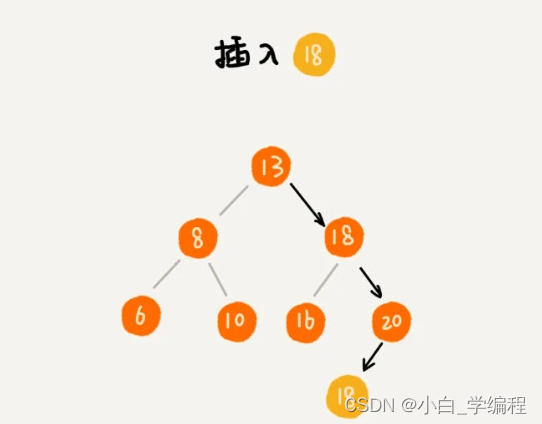
• 当要查找数据的时候，遇到值相同的节点，我们并不停止查找操作，而是继续在右子树中查找，直到遇到叶子节点，才停止。这样就可以把键值等于要查找值的所有节点都找出来。
• 对于删除操作，我们也需要先查找到每个要删除的节点，然后再按前面讲的删除操作的方法，依次删除。

1.5二叉查找树的性能分析

对于同一组数据，我们可以构造不同的二叉查找树

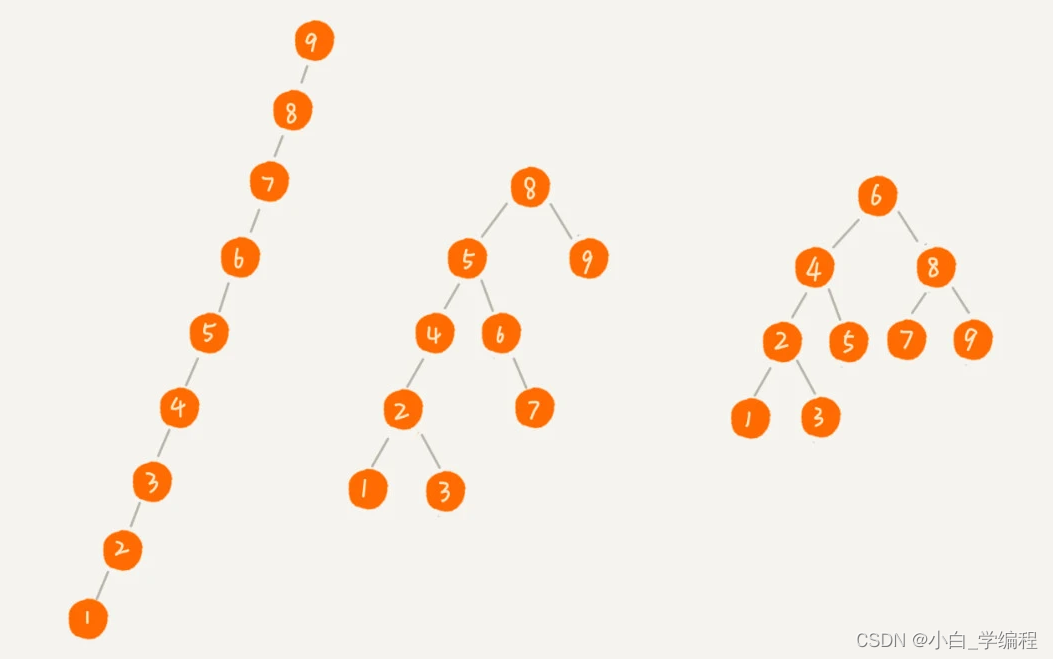
不管操作是插入、删除还是查找，时间复杂度其实都跟树的高度成正比

第一种二叉查找树，根节点的左右子树极度不平衡，已经退化成了链表，所以查找的时间复杂度就变成了O(n)。 

最理想的情况下二叉查找树是一棵完全二叉树（或满二叉树），如上图第三种，插入、删除、查找操作的时间复杂度是O(logn)。

二.平衡二叉查找树

二叉查找树在频繁的动态更新过程中，可能会出现树的高度远大于log n的情况，从而导致各个操作的效率下降。为了避免时间复杂度的退化，针对二叉查找树，引出了一种更加复杂的树，平衡二叉查找树，时间复杂度可以做到稳定的O(logn)

2.1定义

平衡二叉树的严格定义：二叉树中任意一个节点的左右子树的高度相差不能大于1。

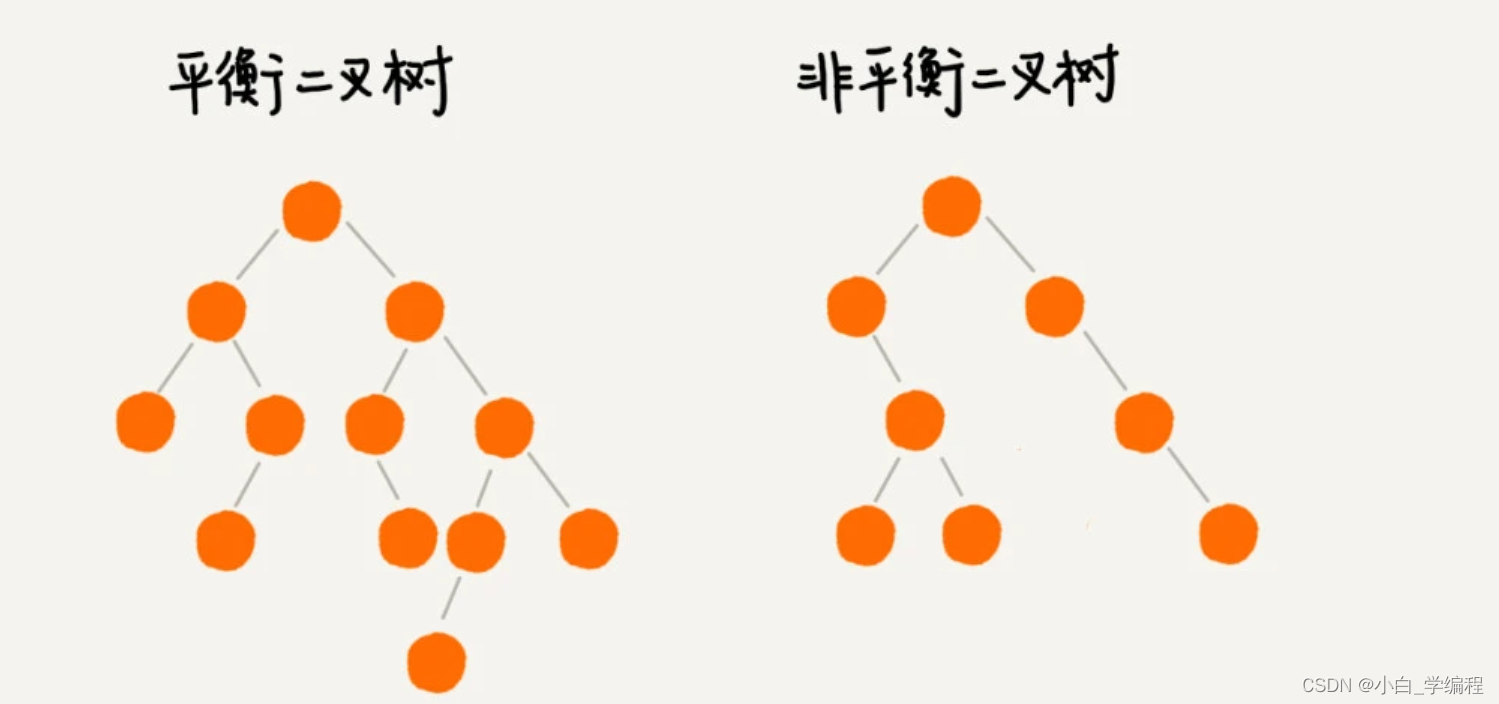
平衡二叉查找树中“平衡”的意思，其实就是让整棵树左右看起来比较“对称”、比较“平衡”，不要出现左子树很高、右子树很矮的情况。这样就能让整棵树的高度相对来说低一些，相应的插入、删除、查找等操作的效率高一些。

2.2红黑树

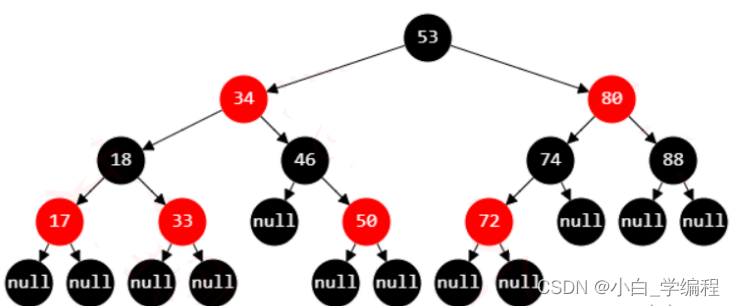
红黑树是平衡二叉树的一种，红黑树中的节点，一类被标记为黑色，一类被标记为红色。除此之外，一棵红黑树还需要满足这样几个要求：

• 根节点是黑色的；

• 每个叶子节点都是黑色的空节点（NIL），也就是说，叶子节点不存储数据；

• 任何相邻的节点都不能同时为红色，也就是说，红色节点是被黑色节点隔开的；

• 每个节点，从该节点到达其可达叶子节点的所有路径，都包含相同数目的黑色节点；

 当然红黑树同时还要满足二叉查找树的特点

2.3为什么红黑树这么受欢迎

平衡二叉查找树其实有很多，比如AVL（严格符合平衡二叉树的定义）、Splay Tree（伸展树）、Treap（树堆）等，但是在实际工程开发中，对于很多需要平衡二叉查找树的地方，更多会选择使用红黑树。

• Treap、Splay Tree，绝大部分情况下，它们操作的效率都很高，但是也无法避免极端情况下时间复杂度的退化。尽管这种情况出现的概率不大，但是对于单次操作时间非常敏感的场景来说，它们并不适用。
• AVL树是一种高度平衡的二叉树，所以查找的效率非常高，但是，有利就有弊，AVL树为了维持这种高度的平衡，就要付出更多的代价。每次插入、删除都要做调整，就比较复杂、耗时。所以，对于有频繁的插入、删除操作的数据集合，使用AVL树的代价就有点高了。当然如果是插入特别少，查询特别多的情况下推荐使用AVL树。
• 而红黑树只是做到了近似平衡，并不是严格的平衡（“平衡”的意思可以等价为性能不退化。“近似平衡”就等价为性能不会退化的太严重），但树的高度仍然是对数量级的，因此性能的损失并不多，并且红黑树降低了对旋转的要求，在插入时避免了大量的旋转，提高了插入,删除的操作性能，所以在维护平衡的成本上，要比AVL树要低。对于工程应用来说，要面对各种异常情况，为了支撑这种工业级的应用，我们更倾向于这种性能稳定的平衡二叉查找树。

三.哈希表为什么不能替代二叉查找树

散列表的插入、删除、查找操作的时间复杂度可以做到常量级的O(1)，非常高效。而二叉查找树在比较平衡的情况下，插入、删除、查找操作时间复杂度才是O(logn)，相对散列表，好像并没有什么优势。那为什么还要用二叉查找树呢？

1. 散列表中的数据是无序存储的，如果要输出有序的数据，需要先进行排序或者配合有序链表来使用。而对于二叉查找树来说，我们只需要中序遍历，就可以在O(n)的时间复杂度内，输出有序的数据序列。
2. 散列表扩容耗时很多，而且当遇到散列冲突时，性能不稳定，尽管二叉查找树的性能不稳定，但是在工程中，我们最常用的平衡二叉查找树的性能非常稳定，时间复杂度稳定在O(logn)。
3. 散列表的构造比二叉查找树要复杂，需要考虑的东西很多。比如散列函数的设计、冲突解决办法、扩容、缩容等。平衡二叉查找树只需要考虑平衡性这一个问题，而且这个问题的解决方案比较成熟、固定。

四.MySQL数据库索引是如何实现的

• 功能性需求比如常见的按值查询和区间查询
• 性能方面的需求，我们主要考察时间和空间两方面，也就是执行效率和存储空间。在执行效率方面，我们希望通过索引，查询数据的效率尽可能的高；在存储空间方面，我们希望索引不要消耗太多的内存空间。

基于数组的解决方案

• 查找的效率很慢
• 在查找时如果设计插入或删除，算法开销很高
• 文件系统和数据库的索引都是存在硬盘上的，并且如果数据量大的话，不一定能一次性加载到内存中

基于哈希的解决方案

• hash冲突后，数据散列不均匀，产生大量线性查询，效率低

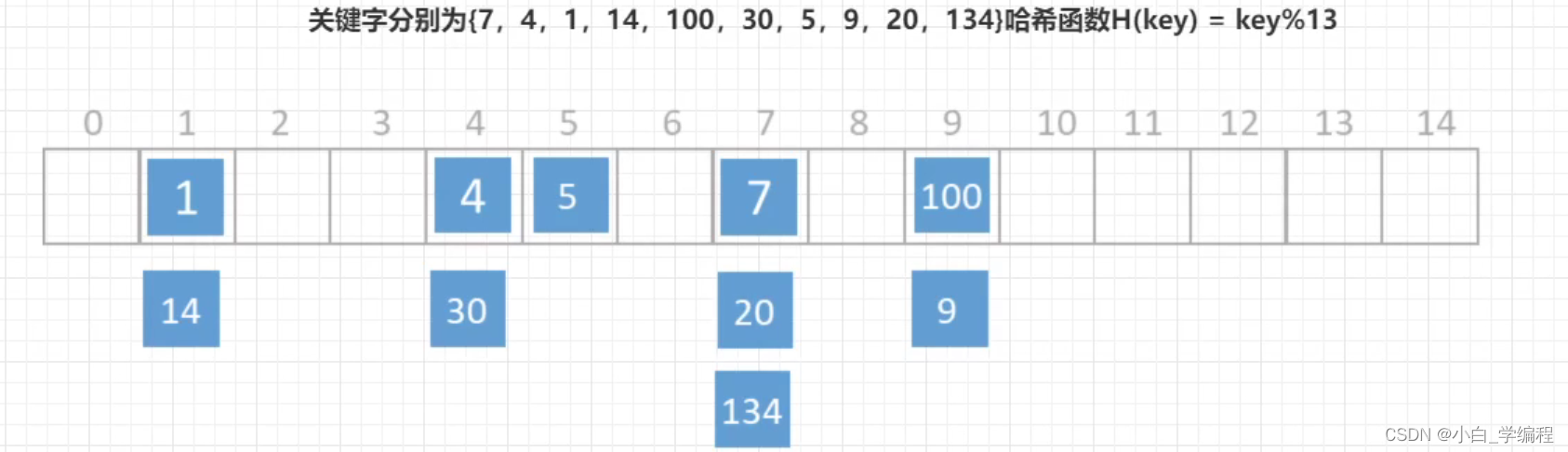
• 等值查询可以，但是不支持区间快速查找数据，只能挨个遍历

基于平衡二叉查找树的解决方案

• 尽管平衡二叉查找树查询的性能也很高，时间复杂度是O(logn)。而且，对树进行中序遍历，我们还可以得到一个从小到大有序的数据序列，但这仍然不足以支持按照区间快速查找数据。
• 当数据量比较大的时候，树的深度会变深，查找的次数也会变多，IO的次数也会变多，影响读取的效率。总结：红黑树不适合IO级别的操作,更适合内存级别的应用。

比如Java中：

• TreeMap、TreeSet都使用红黑树作为底层数据结构
• JDK 1.8开始，HashMap也引入了红黑树：当冲突的链表长度超过8时，自动转为红黑树

有人可能会疑惑为什么这里会涉及到IO次数呢？假设给一亿个数据构建二叉查找树索引，那索引中会包含大约1亿个节点，每个节点假设占用16个字节，那就需要大约1GB的内存空间。给一张表建立索引，我们需要1GB的内存空间。如果我们要给10张表建立索引，那对内存的需求是无法满足的。所以文件系统的索引都是保存在磁盘当中的。

影响IO效率的因素

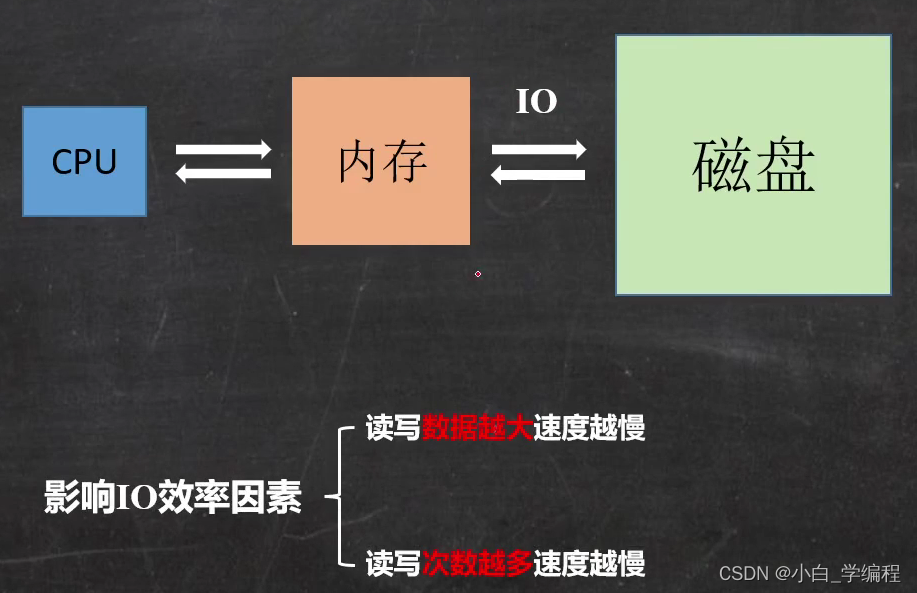
 为了降低树的高度，所以我们引出了B树

B树

B树是一种多路搜索树，它的每个节点可以拥有多于两个孩子节点。M路的B树最多能拥有M个孩子节点（即最多有M-1个关键字）

特点

• 除根节点外，其他节点至少有M/2（向上取整）个孩子节点
• 每个结点的值(索引) 都是按递增次序排列存放的，并遵循左小右大原则。
• 根结点 的 子节点 个数为 [2，M]。
• B树的所有叶子结点都位于同一层。

每个节点的结构

示例

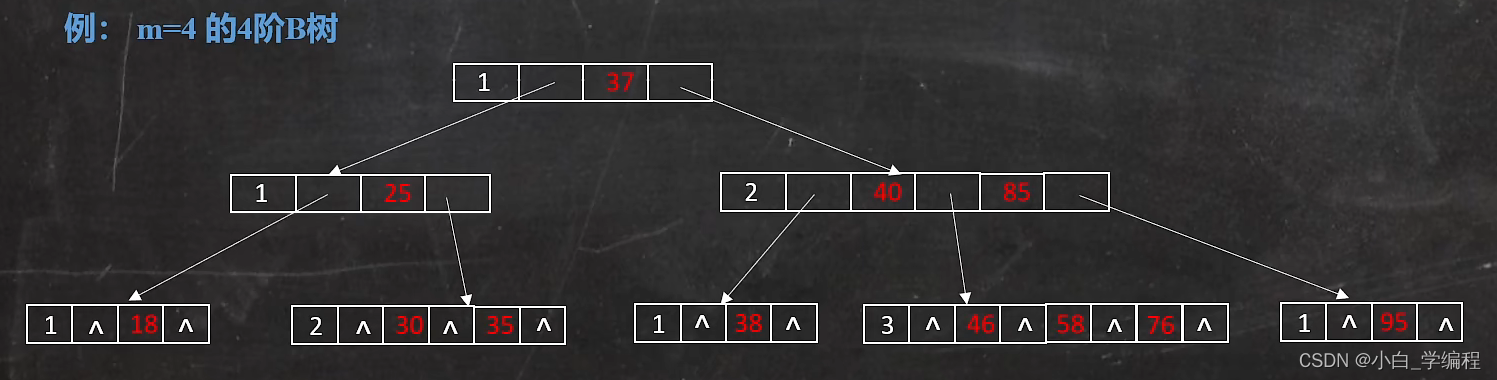
磁盘预读知识补充

当内存读取B文件索引时，程序需要将根节点从磁盘读取到内存中。如果下一个子节点也存储在磁盘中，程序需要从磁盘中读取该节点。为了减少磁盘I/O操作的次数，程序通常会将多个磁盘块读入内存中，这些块中至少包含下一个要访问的子节点。这个操作被称为预读。

如果B文件的节点和数据存储在不同的磁盘块中，程序可能需要多次从磁盘中读取数据才能获取完整的节点或数据。这会导致频繁的磁盘I/O操作，降低程序的性能。

程序在内存中访问B文件的节点和数据时，也需要考虑页的大小。如果一个节点或数据的大小超过了一页的大小，程序需要将其分成多个段，每个段存储在不同的页中。这个过程被称为分页或分块。

概念解析

页（datapage）：页是内存操作的基本单位，页一般由操作系统决定是多大，一般是4k。我们在数据交互时，可以取页的整数倍来进行读取。

我们可以看一个word文档的属性

 实际大小只有11.5KB，但是占用空间却是12.0KB（4的倍数）

磁盘块：磁盘块是文件系统用来管理磁盘空间的基本单位。

• 在虚拟存储器中，操作系统将内存分成若干个页，也将磁盘分成若干个磁盘块，以便将数据从磁盘读入内存或将数据从内存写入磁盘时进行管理。
• 在文件系统中，文件通常被分成若干个磁盘块进行存储，而当程序需要读取文件时，操作系统将磁盘块逐一读入内存中的页中，以便程序能够对文件进行访问。

B树的查找

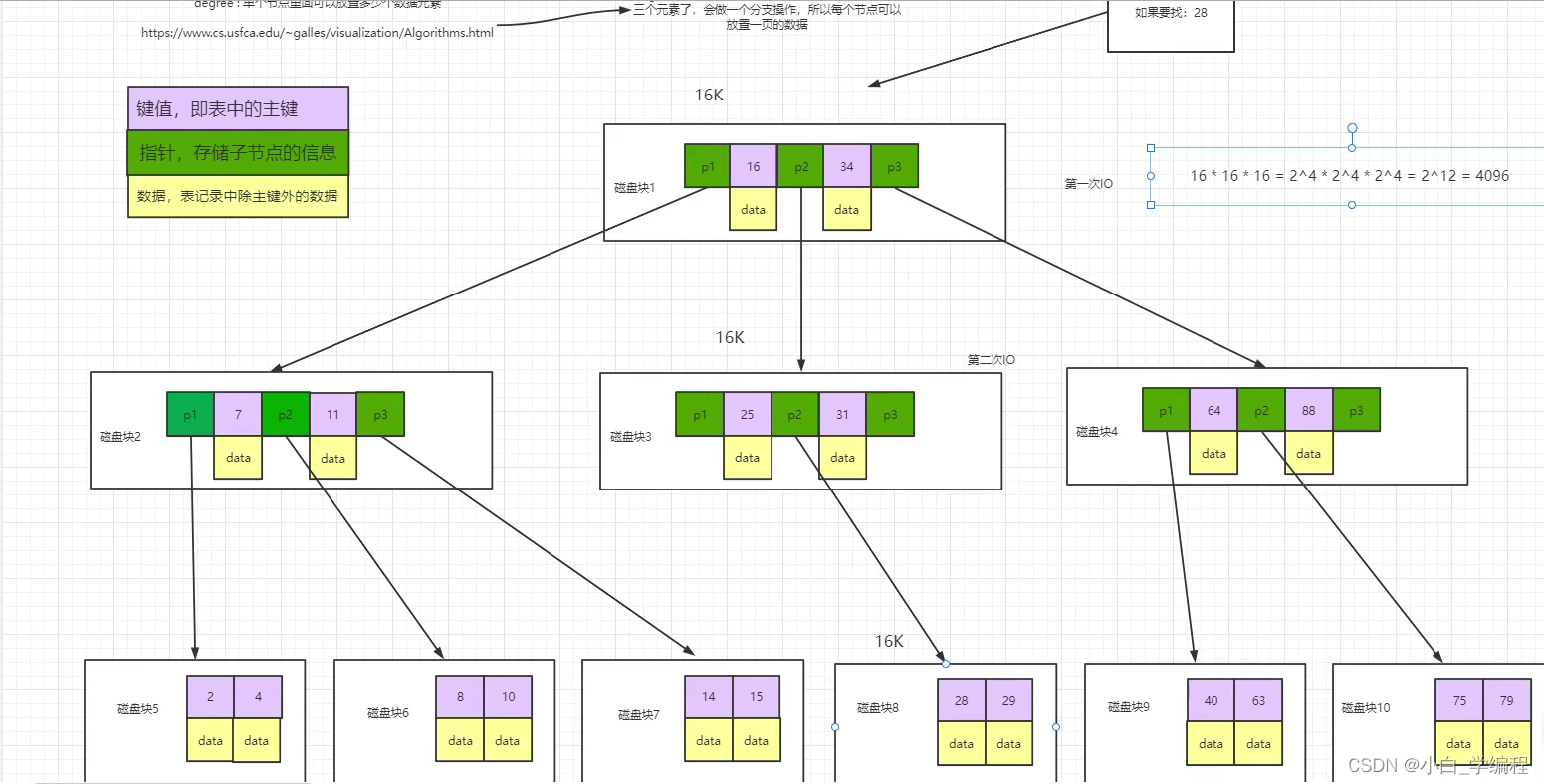
B树中每个节点都可以存放表的行记录数据，每个节点的读取可以视为一次I/O读取，树的高度表示最多的I/O次数，在相同数量的总记录个数下，每个节点的记录个数越多，高度越低，查询所需的I/O次数越少；假设，硬盘一次I/O数据为16K，一条记录占1K，理论上一个节点最多可以放16个记录，16 ×16 ×16 = 2^12=4096条，当需要存100000条数据时，依然可能导致树高度剧增。

我们可以发现节点的data部分其实占了很大的空间，相比之下指针部分和关键字部分占得却很少。为了进一步提高磁盘的访问效率，就产生了B+树

B+树

B+树与B树最大的不同是内部结点不保存记录数据，只保存关键字，用于查找，所有记录数据都保存在叶子结点中。由于每个非叶子节点只存放关键字，这样节点中能存放的关键字数量就更多，树的结构就更加矮小，访问磁盘的次数就更少。

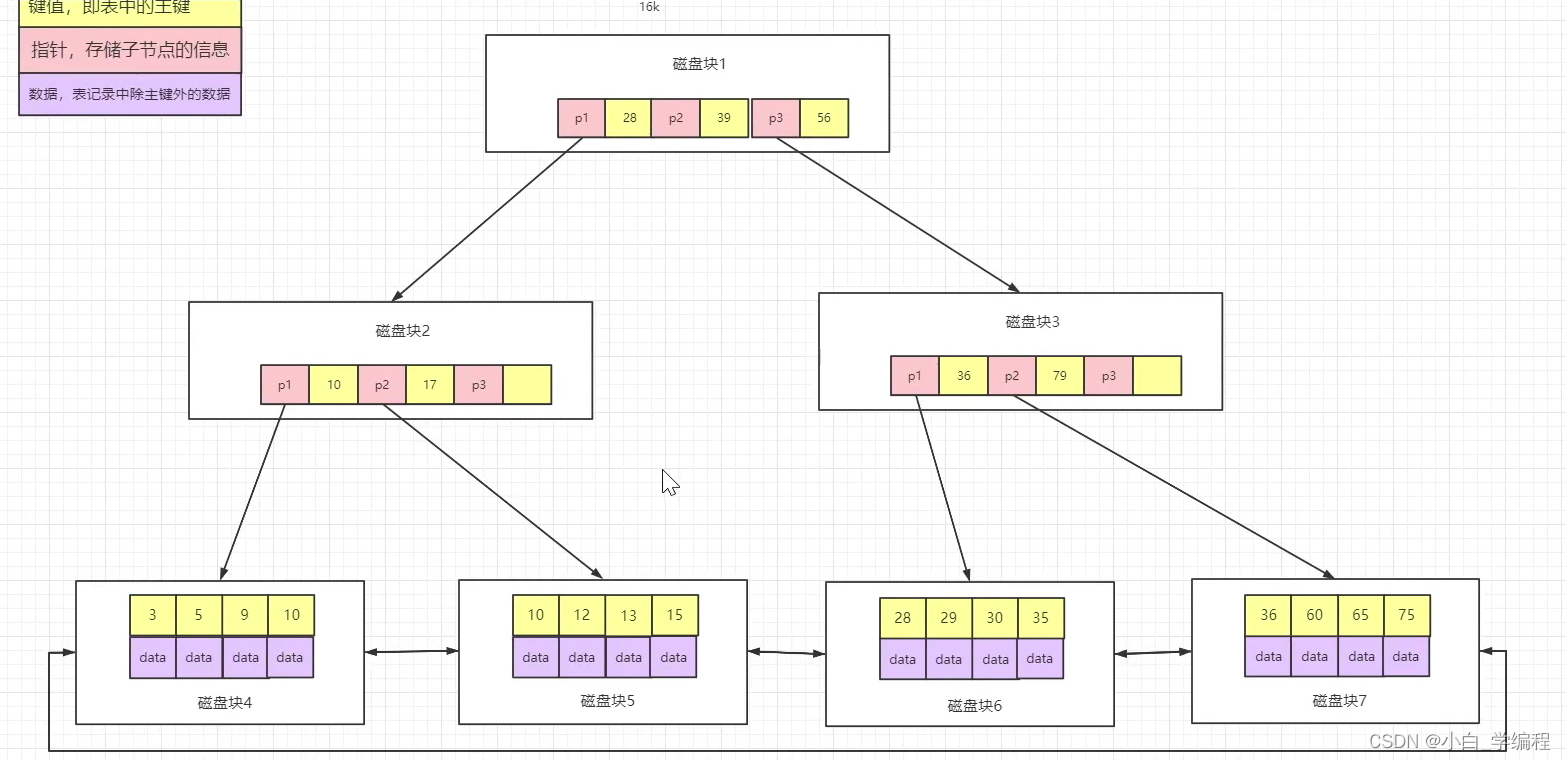
特点 

• B+树中的节点不存储数据，只是索引，而B树中的节点存储数据；

• 通过双向链表将叶子节点串联在一起，这样可以方便按区间查找；

• 每个节点中子节点的个数不能超过m，也不能小于m/2；

• 根节点的子节点个数可以不超过m/2，这是一个例外；

B+树与B树的设计主要用于提高I/O速度，也就是读取磁盘的速度。查询I/O次数越少，速度越快。但B+树的IO性能更高。另外如果涉及到范围查找， B+ 树由于所有数据都在叶子结点，不用跨层，同时由于有链表结构，只需要找到首尾，通过链表就能把所有数据取出来了，查询性能更高。

所以MySQL索引用的是B+树