题目描述

给你一个有 n 个节点的 有向无环图（DAG），请你找出所有从节点 0 到节点 n-1 的路径并输出（不要求按特定顺序）

二维数组的第 i 个数组中的单元都表示有向图中 i 号节点所能到达的下一些节点，空就是没有下一个结点了。

译者注：有向图是有方向的，即规定了 a→b 你就不能从 b→a 。

来源：力扣（LeetCode） 链接：https://leetcode-cn.com/problems/all-paths-from-source-to-target
示例1

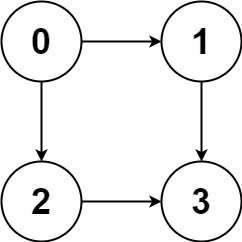
输入：graph = [[1,2],[3],[3],[]]
输出：[[0,1,3],[0,2,3]]
解释：有两条路径 0 -> 1 -> 3 和 0 -> 2 -> 3

示例2

输入：graph = [[4,3,1],[3,2,4],[3],[4],[]]
输出：[[0,4],[0,3,4],[0,1,3,4],[0,1,2,3,4],[0,1,4]]

示例3
输入：graph = [[1],[]]
输出：[[0,1]]

示例4
输入：graph = [[1,2,3],[2],[3],[]]
输出：[[0,1,2,3],[0,2,3],[0,3]]

示例5
输入：graph = [[1,3],[2],[3],[]]
输出：[[0,1,2,3],[0,3]]

解题思路

看到本题，我们首先想到的就是利用深度优先搜索的方式求出所有可能的路径。具体方式为：从0号出发，使用栈记录路径上的点，每次遍历到点n-1，就将栈中记录的路径添加到答案中。

又因为本题是一个有向无环图，因此不用判断节点是否遍历过。代码如下：

# -*- coding: utf-8 -*-## -------------------------------------------------------------------------------
# Name:         797. 所有可能的路径
# Description:
# Author:       PANG
# Date:         2021/8/25
# -------------------------------------------------------------------------------
from typing import Listclass Solution:def allPathsSourceTarget(self, graph: List[List[int]]) -> List[List[int]]:paths = list()stack = list()def dfs(x: int):if x == len(graph) - 1:paths.append(stack[:])returnfor y in graph[x]:stack.append(y)dfs(y)stack.pop()stack.append(0)dfs(0)return pathsif __name__ == '__main__':graph = [[1, 2], [3], [3], []]solution = Solution()print(solution.allPathsSourceTarget(graph))

复杂度分析

• 时间复杂度：$O(n\times 2^n)$，其中 n 为图中点的数量。一种最坏情况是每一个点都可以去往编号比它大的点。此时路径数为 $O(2^n)$，且每条路径长度为 $O(n)$，因此总时间复杂度为 $O(n\times 2^n)$。
• 空间复杂度：$O(n)$，其中 n 为点的数量。主要为栈空间的开销。返回值不计入空间复杂度。