大体思路是从终点反向做一次BFS得到一个层次图,然后从起点开始依次向更小的层跑,跑的时候选则字典序最小的,由于可能有多个满足条件的点,所以要把这层满足条件的点保存起来,在跑下一层。跑完一层就会得到这层最小的color号。
反省:这道题由于有自环和重边的存在,因此满足条件的一个点可能多次被加到队列,这样的复杂度将会成指数级。没注意到这点TLE了几发。。。如果一个点到另一个点的最短路径只有一条,就不用判断重复了。正是因为重边所以特别需要注意这点
示意图:
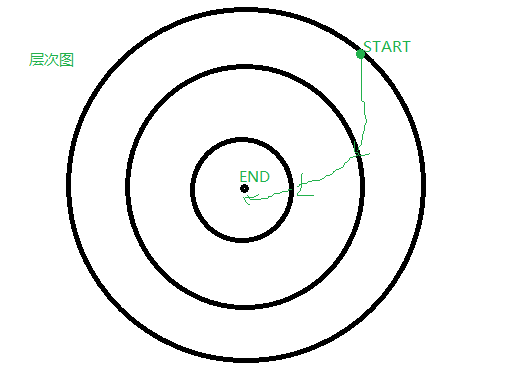
学习点:
1.层次图的构建,逆向思维。
2.注意不是简单图的情况,重边和自环。
3.搜索最致命的问题就是状态判重
#include<cstdio> #include<cstring> #include<vector> #include<queue>//#define local using namespace std; const int INF = 1e9; const int maxm = 2e5 + 10; const int maxn = 1e5 + 5; int n;struct Edge {int v,c,nxt; }e[maxm<<1];int d[maxn]; int cnt , head[maxn];//init head -1 inline void addEdge(int u,int v,int c) {// e[cnt].u = u;e[cnt].v = v;e[cnt].c = c;e[cnt].nxt = head[u];head[u] = cnt++; }void bfs() {queue<int> q;memset(d,-1,sizeof(d));q.push(n); d[n] = 0;int u,v,i;while(!q.empty()){u = q.front(); q.pop();if(u == 1) { printf("%d\n",d[u]); return ;}for(i = head[u]; ~i ; i = e[i].nxt ){v = e[i].v;if(~d[v]) continue;d[v] = d[u] + 1;q.push(v);}} }bool vis[maxn]; void bfs2() {queue<int> q;///复杂度写高了 没有给结点判断重复 指数级int u = 1,v, i;q.push(u);int c = INF;//最小colorvector<int> vec;//保存下一个层次的点memset(vis,false,sizeof(vis));while(!q.empty()||!vec.empty()) {if(q.empty()) { //保证队列里只有一个层次的点,如果队列空了,说明上一层的点都跑完了,这时候c一定是最小的for(i = 0;i < vec.size();i++) {int k = vec[i], v = e[k].v;if(e[k].c == c && !vis[v] ) {//vis[v] 重边if(e[k].v == n) { printf("%d\n",c); return ;}q.push(e[vec[i]].v); vis[v] = true;}}vec.clear();printf("%d ",c); c = INF;}u = q.front(); q.pop();for(i = head[u]; ~i ; i = e[i].nxt ) {v = e[i].v;if(d[u] - d[v] == 1 && e[i].c <= c) {vec.push_back(i);c = e[i].c;}}} }int main() { #ifdef localfreopen("in.txt","r",stdin); #endif // localint m;int u,v,c;while(~scanf("%d%d",&n,&m)){memset(head,-1,sizeof(head)); cnt = 0;while(m--) {scanf("%d%d%d",&u,&v,&c);if(u == v) continue;//忽略自环 addEdge(u,v,c);addEdge(v,u,c);}bfs();bfs2();}return 0; }
