网站建设安全规划免费百度下载
感知机perceptron算法是Frank Rosenblatt于1957年提出,它是神经网络和深度学习的起源算法。
感知机接受多个信号,输出一个信号,具体更多原理,请参见这篇博文
本文用python实现三个简单的逻辑电路,实际上这三种逻辑门电路用感知机实现都不是唯一的,都可以有很多种实现方式(区别只是权重和偏置不一样);且三个门电路之间也只是权重偏置不一样,代码实际上是一样的,也就是感知机的结构都一样,如下图:
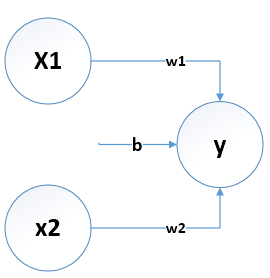
三种门电路的感知机结构如上图,均为2输入单输出,
(1)y={0,x1w1+x2w2+b≤01,x1w1+x2w2+b>0y=\left\{ \begin{aligned} 0&,&x_1w_1+x_2w_2+b\leq0\\ 1&,&x_1w_1+x_2w_2+b>0\\ \end{aligned} \right.\tag1y={01,,x1w1+x2w2+b≤0x1w1+x2w2+b>0(1)
权重w1,w2表示各个输入的重要程度。
偏置b表示神经元激活的难易程度,b越大则越易被激活。
(1)式描述的是一条直线把二维空间线性地分割为两部分。
实际上,如果引入激活函数的概念,则感知机使用的激活函数是阶跃函数:
h(x)={0,x≤01,x>0h(x)=\left\{ \begin{aligned} 0,x\leq0\\ 1,x>0\\ \end{aligned} \right.h(x)={0,x≤01,x>0
激活函数就是连接NN和感知机的桥梁。
感知机使用阶跃函数作激活函数,而只要把激活函数换成其他函数(sigmoid或Relu),就得到了NN.
一、与门(AND gate)
真值表
| x1x_1x1 | x2x_2x2 | y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
代入(1)则有:
{b≤0w2+b≤0w1+b≤0w1+w2+b>0\left\{ \begin{aligned} b\leq0\\ w_2+b\leq0\\ w_1+b\leq0\\ w_1+w_2+b>0 \end{aligned} \right.⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧b≤0w2+b≤0w1+b≤0w1+w2+b>0
满足这组关系的w1,w2,b{w_1,w_2,b}w1,w2,b很多,我们取0.5,0.5,-0.7

import numpy as np
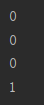
def AND(x1,x2):x = np.array([x1,x2])w = np.array([0.5,0.5])b= -0.7tmp = np.sum(w*x) + bif tmp <= 0:return 0else:return 1print(AND(0,0))
print(AND(0,1))
print(AND(1,0))
print(AND(1,1))
pycharm脚本运行后输出结果:
二、或门(OR gate)
真值表
| x1x_1x1 | x2x_2x2 | y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
代入(1)则有:
{b≤0w2+b>0w1+b>0w1+w2+b>0\left\{ \begin{aligned} b\leq0\\ w_2+b>0\\ w_1+b>0\\ w_1+w_2+b>0 \end{aligned} \right.⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧b≤0w2+b>0w1+b>0w1+w2+b>0
满足这组关系的w1,w2,b{w_1,w_2,b}w1,w2,b很多,我们取0.5,0.5,-0.2

import numpy as np
def OR(x1,x2):x = np.array([x1,x2])w = np.array([0.5,0.5])b = -0.2tmp = np.sum(w*x) + bif tmp <= 0:return 0else:return 1print(OR(0,0))
print(OR(0,1))
print(OR(1,0))
print(OR(1,1))
pycharm脚本运行后输出结果:
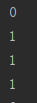
三、与非门(NAND gate)
真值表
| x1x_1x1 | x2x_2x2 | y |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
代入(1)则有:
{b>0w2+b>0w1+b>0w1+w2+b≤0\left\{ \begin{aligned} b>0\\ w_2+b>0\\ w_1+b>0\\ w_1+w_2+b\leq0 \end{aligned} \right.⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧b>0w2+b>0w1+b>0w1+w2+b≤0
满足这组关系的w1,w2,b{w_1,w_2,b}w1,w2,b很多,我们取-0.5,-0.5,0.7

import numpy as np
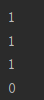
def NAND(x1,x2):x = np.array([x1,x2])w = np.array([-0.5,-0.5])b = 0.7tmp = np.sum(w*x) + bif tmp <= 0:return 0else:return 1print(NAND(0,0))
print(NAND(0,1))
print(NAND(1,0))
print(NAND(1,1))
pycharm脚本运行后输出结果:
如上,单层感知机只能表示线性的空间划分,对于异或门,单层感知机则无法通过简单的一条直线划分开。这就是单层感知机的局限性。
四、异或门
真值表
| x1x_1x1 | x2x_2x2 | y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
学习数电时我们知道,简单门电路的组合可以实现复杂的门电路。所以:

def XOR(x1,x2):s1 = NAND(x1,x2)s2 = OR(x1,x2)y = AND(s1,s2)return yprint(XOR(0,0))
print(XOR(0,1))
print(XOR(1,0))
print(XOR(1,1))
pycharm脚本运行后输出结果:
异或门是一个两层的感知机:

总结:
- 可以看出,单层感知机无法表示的东西,加一层就解决了,所以加深层可以进行更复杂更灵活的表示,这就是深度神经网络可以学到复杂表示的理论源头。
- 本文实现的感知机的权重都是人工设置的,如果用感知机实现复杂的函数,权重的人工确定十分困难。而这个问题的解决就引入了神经网络,或者说神经网络解决了这个问题。因为NN的重要性质是他可以自动从数据中学得合适的参数(权重,偏置)。
