品牌网站建设解决方案短视频营销方式有哪些

隐马尔科夫实现：

前文链接：https://my.oschina.net/u/3268732/blog/1480198

如前文的说法，隐马尔科夫相关的有两个式子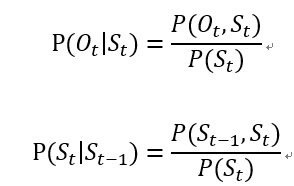： 对两个式子就可以建立矩阵A，矩阵B。矩阵A是S之间的转换，为NN,N为标签个数，矩阵中的值为当前标签转移至下一标签的概率。矩阵B是S与O之间的转化，为NM，M为O的可能状态，实际上就是在求每个状态下转移的概率。模型中还有一个值π，寓意为每个标签出现的可能性。

下面对一个解码问题进行说明：

解码问题用维特比算法，可应用与文本信息抽取，还有什么基因检测，蛋白质二级序列啥的……解码问题有很多优化，如CRF等，真实工程中就不会用这种原始的了……。对于序列上的每一个元素，其转换可能为标签里的任意一种，同时，他被下一元素限制，因为下一元素也是一种转化的表现。所以大体思路就是先算所有词的转化标签概率（记得考虑自身和上一词两种情况），形成一个树状结构。（图示如李航《统计学习方法》P186）这个时候就是递推，一直推完。然后只需在这所有的路径里找到最优的方案，也就是所有概率最优的情况。

第一步：构建一个模型：

这一步直接就是对训练数据进行统计就完了

第二步：进行维特比算法：

算法：

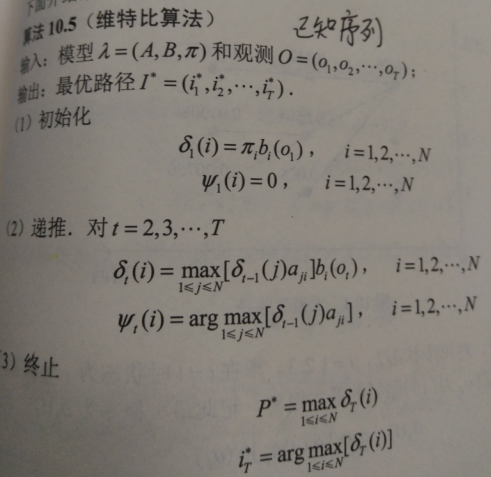
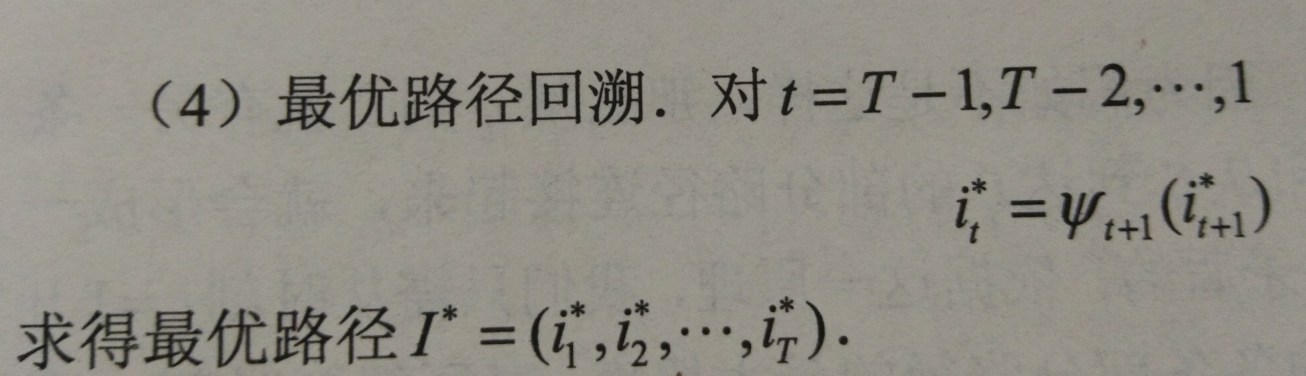代码：

#统计a,pi
def HMMA():for i in range(len(label)):#初始化计数countp=[]s=0for j in range(len(label)):countp.append(0)for j in range(trainlen-1):if(trainos[j+1]==label[i]):s+=1countp[label.index(trainos[j])]+=1for j in range(len(label)):if(s!=0):a[i].append(countp[j]/s)else:a[i].append(0)#初始初始矩阵pi.append(s/trainlen)global bb=proyx#统计b
def HMMB():count=[]for i in range(len(label)):countall=0for j in range(len(trainx)):count.append(0)for j in range(trainlen):if(trainos[j]==label[i]):countall+=1count[trainxx.index(trainsq[j])]+=1for j in range(len(trainxx)):hmmb[i].append(count[j]/countall)count=[]#维特比
def viterbi(testsq,testos,b):delta = [[]for i in range(len(testsq))]fai = [[]for i in range(len(testsq))]#初始化if(len(testsq)==0):returnfor i in range(len(label)):if(testsq[0])in trainxx:delta[0].append(pi[i]*b[i][trainxx.index(testsq[0])]*bigger)else:delta[0].append(0)fai[0].append(0)for j in range(1,len(testsq)):for i in range(len(label)):if(testsq[j]) in trainxx:maxtmp=-1max_i=0for k in range(len(label)):if(delta[j-1][k]*a[i][k]>maxtmp):maxtmp=delta[j-1][k]*a[i][k]max_i=kdelta[j].append(maxtmp*b[i][trainxx.index(testsq[j])])fai[j].append(max_i)else:delta[j].append(0)fai[j].append(0)maxtmp=0max_i=0mytestchoic=[]mytestos=[]for i in range(len(label)):if maxtmp<delta[len(testsq)-1][i]:maxtmp=delta[len(testsq)-1][i]max_i=imytestchoic.append(max_i)for i in range(1,len(testsq)):mytestchoic.append(fai[i-1][mytestchoic[i-1]])for i in range(len(testsq)):mytestos.append(label[mytestchoic[i]])print(mytestos)

最大熵隐马模型：

最大熵的方法就是将隐马模型中的B这里的矩阵参数进行优化。另外因为这个模型又要考虑相近状态，所以在这里所有的x相当于当前序列+当前序列标记（xi+yi），y为前一个标签状态（yi-1） 最大熵的就是用来优化似然函数的一种方法，想办法保证全局最优，期望一个最佳最合理的P(y|x)来预测。 特征函数f(x,y)（特征函数，说白了就是一个集合，满足这一条件的xy就判为1，否则为0） 注意：这里仅仅考虑标签只有一类的情况，若是多类情况，则需要分别对每一种特征构造特征模板，所以多类情况时w也是一个二维数组。最后的p(y|x)应对应隐马模型中的B 对于似然函数优化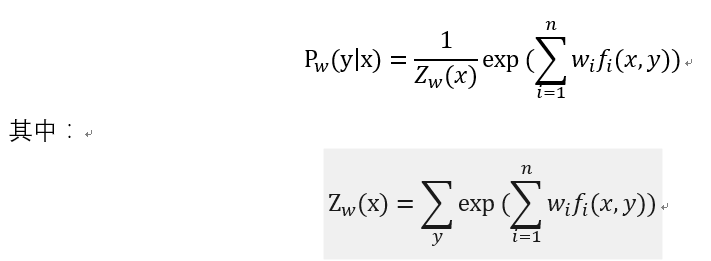： 其中W是可变的，在迭代中会不断变化他的值，Z(x)表示所有特征发生的情况下当前x发生的情况（写程序的时候直接把f（）写成只含0，1的数组不就好了……） 代码：

#各种统计初始
def definef():for i in range(len(label)):M.append(trainos.count(label[i]))for j in range(len(trainx)):f[i].append(0)w[i].append(0)proyx[i].append(0)provx[i].append(0)for i in range(trainlen-1):f[label.index(trainos[i])][trainx.index(str(trainsq[i+1]+trainos[i+1]))]=1def countpos():#对于每个特征找各自概率for i in range(len(label)):countxy=0for j in range(trainlen-1):if(f[i][trainx.index(trainsq[j+1]+trainos[j+1])]==1 and trainos[j]==label[i]):countxy+=1provx[i][trainx.index(trainsq[j+1]+trainos[j+1])]+=1for j in range(len(trainx)):provx[i][j]/=trainlenprovxy[i]=countxy/trainlendef countyxpos():for i in range(len(label)):z=0p=[]for j in range(len(trainx)):p.append(0)for j in range(trainlen-1):if(trainos[j+1]==label[i]):if(f[i][trainx.index(trainsq[j+1]+trainos[j+1])]==1):z+=math.e**(w[i][trainx.index(trainsq[j+1]+trainos[j+1])]*trainx.count(trainsq[j+1]+trainos[j+1]))if (f[i][trainx.index(trainsq[j + 1] + trainos[j + 1])] == 1):p[trainx.index(trainsq[j+1]+trainos[j+1])]+=w[i][trainx.index(trainsq[j+1]+trainos[j+1])]for j in range(len(trainx)):if(z!=0):proyx[i][j]=(math.e**p[j])/z
#开始迭代了
def iterate(times):for i in range(times):for l in range(len(label)):for j in range(len(trainx)):tmp=0if(M[l]!=0 and provx[l][j]*proyx[l][j]*f[l][j]!=0):tmp+=math.log(provxy[l]/provx[l][j]*proyx[l][j]*f[l][j])/M[l]global ww[l][j]+=tmpcountyxpos()print(i)

注意，尽管一个数据可能序列有多条，输出一条标签，这是需要人为将这些标签合成成一条标签。有点狗血……