百度云服务器做asp网站南宁seo主管
如果没看过这篇paper，可以先去看一下翻译过的版本Darts译文
整篇paper主要分了三大部分， 分别是INTRODUCTION、DIFFERENTIABLE ARCHITECTURE SEARCH、EXPERIMENTS AND RESULTS，其中最重要的部分是第二部分——可微的结构搜索。接下来主要从第二部分开始梳理：
2.1 搜索空间
先搜一个一个的小cell（单元网络），然后再叠加这些cell形成一个大的网络。下图中的每个图都是一个cell（由节点0、1、2、3组成），然后边是各种操作，例如卷积、池化、0操作。
现在的问题是如何找到一个最优的cell
2.2 连续松弛优化
2.2主要介绍的就是如何寻找好的参数，也就是说怎么找到上图中的 “ ？”
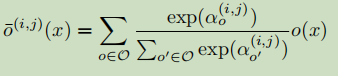求每个操作权重的加权平均
可以发现每个节点上都由三条线，分别代表三种操作，α是一个矩阵，代表所有边的加权值，训练的时候三条边都进行训练，最后结果只选一条边，也就是选权重最大的那一条，在搜索结束时，通过用最有可能的操作替换每个混合运算。然后，结构搜索的任务简化为学习一组连续的变量
， (i,j)表示i和j之间的边。
搜索空间变成连续后，我们就要求最优的α和w（w是结构本来的参数，卷积核中的值），既然是连续的，那么就可以用梯度下降的方法进行求解，一般来说，我们之前的优化都是只优化w，这次变成的两个参数。作者就想通过验证集来优化α，用训练集优化w，就构成了一个双层优化问题。
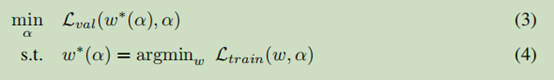
算法：
为每条边（i，j）创建一个由
参数化的混合运算
，相当于初始化。
While 不收敛 {
- 更新体系结构α，通过梯度下降
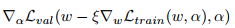
- 更新权值w，通过梯度下降
}
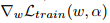
最终获得基于α的体系结构
paper的关键是连续，以前的Nas的搜索空间都是离散的，就是随机挨个的试，所以说效率太低。本文是让α这个参数进去了模型，然后搜索空间就变成连续的了，可以通过梯度下降求最优的α，w，效率肯定变快。
2.3
这个小结就是说通过上面的式子算，精确的计算上面的式子计算量太大，作者就想用简单的式子来近似替换。