目录
1 问题描述
2 解决方案
1 问题描述
问题描述
为二维空间中的点设计一个结构体,在此基础上为三角形设计一个结构体。分别设计独立的函数计算三角形的周长、面积、中心和重心。输入三个点,输出这三个点构成的三角形的周长、面积、外心和重心。结果保留小数点后2位数字。
样例输出
与上面的样例输入对应的输出。
例:
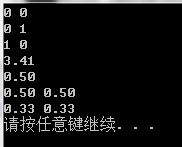
例:
数据规模和约定
输入数据中每一个数的范围。
例:doule型表示数据。
例:doule型表示数据。
2 解决方案
本题主要考查三角形相关数学知识,刚开始做的时候,我对重心和外心的计算公式一点都记不起来,无语中...,后来,计算外心的时候,也出错,因为没有单独划分出横坐标相等的情况,导致计算出错。
![]()
具体代码如下:
import java.util.Scanner;public class Main {//计算三角形三条边的长public double[] getABC(double[][] point) {double[] edge = new double[3];double x1 = point[0][0], y1 = point[0][1];double x2 = point[1][0], y2 = point[1][1];double x3 = point[2][0], y3 = point[2][1];edge[0] = (x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2);edge[0] = Math.sqrt(edge[0]);edge[1] = (x1 - x3) * (x1 - x3) + (y1 - y3) * (y1 - y3);edge[1] = Math.sqrt(edge[1]);edge[2] = (x2 - x3) * (x2 - x3) + (y2 - y3) * (y2 - y3);edge[2] = Math.sqrt(edge[2]);return edge;}//计算三角形的周长public double getL(double[][] point) {double[] edge = getABC(point);return edge[0] + edge[1] + edge[2];}//计算三角形的面积public double getS(double[][] point) {double[] edge = getABC(point);double p = (edge[0] + edge[1] + edge[2]) / 2;double S = p * (p - edge[0]) * (p - edge[1]) * (p - edge[2]); //海伦公式S = Math.sqrt(S);return S;}//计算三角形的外心(PS:三角形外接圆的圆心,外心到三个顶点距离相等)public double[] getExcenter(double[][] point) {double[] center = new double[2];double x1 = point[0][0], y1 = point[0][1];double x2 = point[1][0], y2 = point[1][1];double x3 = point[2][0], y3 = point[2][1];double a , b , c , d ;a = (x1*x1 + y1*y1 - x2*x2 - y2*y2) * (x1 - x3) / 2;b = (x1*x1 + y1*y1 - x3*x3 - y3* y3) * (x1 - x2) / 2;c = (y1 - y2) * (x1 - x3);d = (y1 - y3) * (x1 - x2);center[1] = (a - b) / (c - d); //外心的纵坐标double e, f;if(x1 != x2) { //防止出现两点的横坐标相等的情况e = (x1*x1 + y1*y1 - x2*x2 - y2*y2) / (2 * (x1 - x2));f = (y1 - y2) / (x1 - x2);center[0] = e - f * center[1]; //外心的横坐标} else if(x1 != x3) {e = (x1*x1 + y1*y1 - x3*x3 - y3*y3) / (2 * (x1 - x3));f = (y1 - y3) / (x1 - x3);center[0] = e - f * center[1];} else if(x2 != x3) {e = (x2*x2 + y2*y2 - x3*x3 - y3*y3) / (2 * (x2 - x3));f = (y2 - y3) / (x2 - x3);center[0] = e - f * center[1];}return center; }//计算三角形的重心(PS:三角形中三条边的中线交点)public double[] getBarycenter(double[][] point) {double[] center = new double[2];double x1 = point[0][0], y1 = point[0][1];double x2 = point[1][0], y2 = point[1][1];double x3 = point[2][0], y3 = point[2][1];center[0] = (x1 + x2 + x3) / 3; //重心的横坐标center[1] = (y1 + y2 + y3) / 3; //重心的纵坐标return center;}//输出题意结果public void printResult(double[][] point) {double L = getL(point);double S = getS(point);double[] exCenter = getExcenter(point);double[] baryCenter = getBarycenter(point);System.out.printf("%.2f\n",L);System.out.printf("%.2f\n",S);System.out.printf("%.2f",exCenter[0]);System.out.printf(" %.2f\n",exCenter[1]);System.out.printf("%.2f",baryCenter[0]);System.out.printf(" %.2f\n",baryCenter[1]);}public static void main(String[] args) {Main test = new Main();Scanner in = new Scanner(System.in);double[][] point = new double[3][2];for(int i = 0;i < 3;i++) {point[i][0] = in.nextDouble();point[i][1] = in.nextDouble();}test.printResult(point);} }
