温州做美食网站/网络推广方法有哪几种
维纳滤波器
1. 背景及术语介绍
随机信号或者随机过程：它是是普遍存在的。一方面，任何确定性信号经过测量后往往会引入随机性误差；另一方面，任何信号本身都存在随机干扰。
噪声：按照功率谱密度划分可以划分为白噪声(white noise)和色噪声(color noise)，我们常把均值为0的白噪声叫纯随机信号。
干扰和噪声：非目标信号都可叫干扰。干扰可以是确定信号，如国内的50Hz工频，直流成分，也可以是不确定信号如噪声。因此，干扰包含噪声，但是噪声不包含干扰。
广义平稳过程：信号处理中常用的弱平稳也被称为广义平稳(Wide-Sense Stationary,WSS)、二阶平稳或者协方差平稳。WSS随机过程一阶(期望)和二阶矩(方差)不随时间变化。如果一个随机过程满足下列条件:
随机过程的期望值E[x(t)]为一常数，时间变量无关。
自相关函数1 Rx _xxx _xx(t1 _11,t2 _22)仅为时间差2 _22-1 _11=τ的函数;
如果条件2得到满足，则这样的随机过程称为自相关平稳过程。如果条件1得到满足，则该随机过程有最低形式的平稳性，称为均值平稳。如果随机过程同时满足条件1和2，则称为广义平稳随机过程。
滤波：用当前和过去的观测值来估计当前的信号称为滤波。
预测：用过去的观测值来估计当前和将来的信号。
平滑或内插：用过去的观测值来估计过去的信号。
2. 维纳滤波特点
假设：信号以及附加噪声都是已知频谱特性或者自相关和互相关的随机过程
性能标准：最小均方差
结果：能够用标量的方法找到最优2滤波器，它的解是以传函H(z)或单位冲击h(n)的形式给出，是通过卷积的，适用于平稳系统。
维纳-霍夫方程
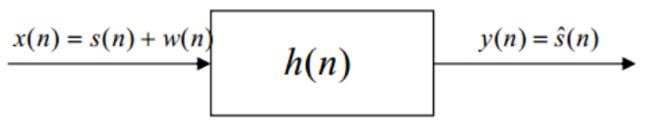x(n)为观测值，它为信号s(n)和噪声w(n)的叠加，经过h(n)滤波后，得到s(n)的观测值s ^ \hat{s}s^(n)。
从图中的系统框图中估计到的观测信号s ^ \hat{s}s^和我们期望得到的真实信号s(n)不可能完全相同，这里用e(n)表示真值和估计值之间的误差。
e ( n ) = s ( n ) − s ^ ( n ) ( 1 ) e(n)=s(n)-\hat{s}(n)\qquad (1)e(n)=s(n)−s^(n)(1)
e(n)为随机变量，维纳滤波器的误差准则为最小均方差。
E [ e 2 ( n ) ] = E [ ( s ( n ) − s ^ ( n ) ) 2 ] ( 2 ) E[e^2(n)]=E[(s(n)-\hat{s}(n))^2]\qquad (2)E[e2(n)]=E[(s(n)−s^(n))2](2)
h(n)是物理可实现的，所以有
h ( n ) = 0 , 当 n < 0 h(n)=0, 当n<0h(n)=0,当n<0
y ( n ) = s ^ ( n ) = ∑ m = 0 + ∞ h ( m ) x ( n − m ) ( 3 ) y(n)=\hat{s}(n)=\sum_{m=0}^{+\infty}h(m)x(n-m)\qquad (3)y(n)=s^(n)=m=0∑+∞h(m)x(n−m)(3)
根据公式(1~3)得：
E [ e 2 ( n ) ] = E [ ( s ( n ) − ∑ m = 0 + ∞ h ( m ) x ( n − m ) ) 2 ] ( 4 ) E[e^2(n)]=E[(s(n)-\sum_{m=0}^{+\infty}h(m)x(n-m))^2]\qquad (4)E[e2(n)]=E[(s(n)−m=0∑+∞h(m)x(n−m))2](4)
要使得均方误差最小，则对(4)各个h(m)求偏导，并且等于零，得：
2 E [ ( s ( n ) − ∑ m = 0 + ∞ h ( m ) o p t x ( n − m ) ) x ( n − j ) ] j = 0 , 1 , 2 , 3... ( 5 ) 2E[(s(n)-\sum_{m=0}^{+\infty}h(m)_{opt}x(n-m))x(n-j)]\quad j=0,1,2,3...\qquad (5)2E[(s(n)−m=0∑+∞h(m)optx(n−m))x(n−j)]j=0,1,2,3...(5)
用相关函数R来表示上式，则得到维纳-霍夫方程的离散形式:
R s x ( j ) = ∑ m = 0 + ∞ h ( m ) o p t R x x ( j − m ) j = 0 , 1 , 2 , 3... ( 6 ) R_{sx}(j)=\sum_{m=0}^{+\infty}h(m)_{opt}R_{xx}(j-m)\quad j=0,1,2,3...\qquad (6)Rsx(j)=m=0∑+∞h(m)optRxx(j−m)j=0,1,2,3...(6)
从维纳-霍夫方程中解出的h就是最小均方差下的最佳h。
有限脉冲响(FIR, Finite Impulse Response)应法求解维纳-霍夫方程
设h(n)是一个因果序列且可以用有限长(N)的序列去逼近它，则得到：
y ( n ) = s ^ ( n ) = ∑ m = 0 N − 1 h ( m ) x ( n − m ) ( 7 ) y(n)=\hat{s}(n)=\sum_{m=0}^{N-1}h(m)x(n-m)\qquad (7)y(n)=s^(n)=m=0∑N−1h(m)x(n−m)(7)
E [ e 2 ( n ) ] = E [ ( s ( n ) − ∑ m = 0 N − 1 h ( m ) x ( n − m ) ) 2 ] ( 8 ) E[e^2(n)]=E[(s(n)-\sum_{m=0}^{N-1}h(m)x(n-m))^2]\qquad (8)E[e2(n)]=E[(s(n)−m=0∑N−1h(m)x(n−m))2](8)
2 E [ ( s ( n ) − ∑ m = 0 N − 1 h ( m ) o p t x ( n − m ) ) x ( n − j ) ] j = 0 , 1 , 2 , 3... N − 1 ( 9 ) 2E[(s(n)-\sum_{m=0}^{N-1}h(m)_{opt}x(n-m))x(n-j)]\quad j=0,1,2,3...N-1\qquad (9)2E[(s(n)−m=0∑N−1h(m)optx(n−m))x(n−j)]j=0,1,2,3...N−1(9)
E [ s ( n ) x ( n − j ) ] = ∑ m = 0 N − 1 h ( m ) o p t x ( n − m ) x ( n − j ) j = 0 , 1 , 2 , 3... N − 1 ( 9 ) E[s(n)x(n-j)]=\sum_{m=0}^{N-1}h(m)_{opt}x(n-m)x(n-j)\quad j=0,1,2,3...N-1\qquad (9)E[s(n)x(n−j)]=m=0∑N−1h(m)optx(n−m)x(n−j)j=0,1,2,3...N−1(9)
R s x ( j ) = ∑ m = 0 N − 1 h ( m ) o p t R x x ( j − m ) j = 0 , 1 , 2 , 3... N − 1 ( 10 ) R_{sx}(j)=\sum_{m=0}^{N-1}h(m)_{opt}R_{xx}(j-m)\quad j=0,1,2,3...N-1\qquad (10)Rsx(j)=m=0∑N−1h(m)optRxx(j−m)j=0,1,2,3...N−1(10)
于是展开后得到N个线性方程，最终可得
{ j = 0 R s x ( 0 ) = h ( 0 ) o p t * R x x ( 0 ) + h ( 1 ) o p t * R x x ( 1 ) +...+ h ( N − 1 ) o p t * R x x ( N − 1 ) j = 1 R s x ( 1 ) = h ( 0 ) o p t * R x x ( 1 ) + h ( 1 ) o p t * R x x ( 0 ) +...+ h ( N − 1 ) o p t * R x x ( N − 2 ) . . . ... j = N − 1 R s x ( 1 ) = h ( 0 ) o p t * R x x ( N − 1 ) + h ( 1 ) o p t * R x x ( N − 2 ) +...+ h ( N − 1 ) o p t * R x x ( 0 ) \begin{cases} j=0& \text{$R_{sx}(0)$=$h(0)_{opt}$*$R_{xx}(0)$+$h(1)_{opt}$*$R_{xx}(1)$+...+$h(N-1)_{opt}$*$R_{xx}(N-1)$}\\ j=1& \text{$R_{sx}(1)$=$h(0)_{opt}$*$R_{xx}(1)$+$h(1)_{opt}$*$R_{xx}(0)$+...+$h(N-1)_{opt}$*$R_{xx}(N-2)$}\\ ...& \text{...}\\ j=N-1& \text{$R_{sx}(1)$=$h(0)_{opt}$*$R_{xx}(N-1)$+$h(1)_{opt}$*$R_{xx}(N-2)$+...+$h(N-1)_{opt}$*$R_{xx}(0)$} \end{cases}⎩⎪⎪⎪⎨⎪⎪⎪⎧j=0j=1...j=N−1Rsx(0)=h(0)opt*Rxx(0)+h(1)opt*Rxx(1)+...+h(N−1)opt*Rxx(N−1)Rsx(1)=h(0)opt*Rxx(1)+h(1)opt*Rxx(0)+...+h(N−1)opt*Rxx(N−2)...Rsx(1)=h(0)opt*Rxx(N−1)+h(1)opt*Rxx(N−2)+...+h(N−1)opt*Rxx(0)
简化形式：
R x x H = R x s R_{xx}H=R_{xs}RxxH=Rxs
R x x R_{xx}Rxx是自相关矩阵，H=[h(0),h(1),…,h(N-1)]'是待求得单位脉冲响应。R x s R_{xs}Rxs=[R x s R_{xs}Rxs(0),R x s R_{xs}Rxs(1),…,R x s R_{xs}Rxs(N-1)]'是互相关序列。
若信号s和噪声w互不相关,则R s w R_{sw}Rsw(m) = R w s R_{ws}Rws(m) = 0。
R x s R_{xs}Rxs(m) = E[x(n)s(n+m)] = E[(s(n)+w(n))s(n+m)] = R s s R_{ss}Rss(m)
R x x R_{xx}Rxx(m) = E[x(n)x(n+m)] = E[(s(n)+w(n))(s(n)+w(n))] = R s s R_{ss}Rss(m)+R w w R_{ww}Rww(m)
E [ e 2 ( n ) ] m i n = R s s ( 0 ) − ∑ m = 0 N − 1 h o p t ( m ) R s s ( m ) E[e^2(n)]_{min}=R_{ss}(0)-\sum_{m=0}^{N-1}h_{opt}(m)R_{ss}(m)E[e2(n)]min=Rss(0)−m=0∑N−1hopt(m)Rss(m)
参考代码
原信号：x = Aec o s ( 2 π ∗ f ∗ t / f s ) ^{cos(2\pi*f*t/fs)}cos(2π∗f∗t/fs)+b
噪声：强度为1dBW的高斯白噪声
A = 1; %信号的幅值
b = 2; %信号偏移项
f = 2000; %信号的频率
fs = 10^5; %采样信号的频率
t=(0:999); %采样点
Mlag = 1000; %滤波器的长度
x=A*exp(cos(2*pi*f*t/fs))+b; %输入正弦波信号
noise=wgn(1,1000,1); %产生1行1000列的高斯白噪声矩阵，输出强度为1dBW
xn=x+noise;
figure(1);
subplot(411);
plot(x)
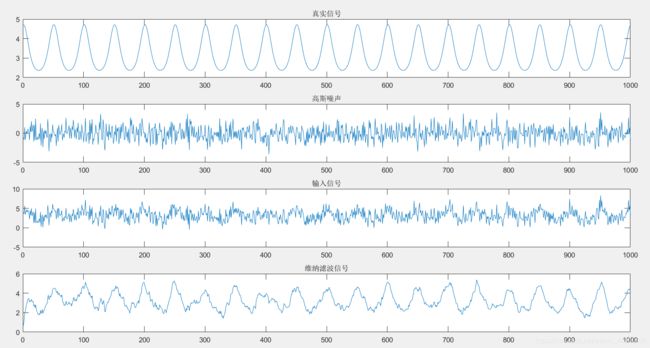
title('真实信号')
subplot(412);
plot(noise)
title('高斯噪声')
subplot(413);
plot(xn)
title('输入信号')
%维纳滤波
N = 1000;
Rxn = xcorr(xn,Mlag,'biased');%自相关函数，Mlag为长度
Rnxn = xcorr(xn,x,Mlag,'biased');%互相关函数
rnxn = Rnxn(1001:1001+N-1)';
rxn = diag(Rxn(1001)*ones(1,N));
for i = 1:N-1
kk = Rxn(1001+i)*ones(1,N-i);
rxn = rxn + diag(kk,i)+diag(kk,-i);
end
h = inv(rxn)*rnxn;
y = filter(h,1,xn);
y2 = conv(xn,h); %另一种求法(和用filter结果一样，取前一半)
subplot(414);
plot(y)
title('维纳滤波信号')
figure(3)
subplot(311)
[f,xi]=ksdensity(x)
plot(xi,f)
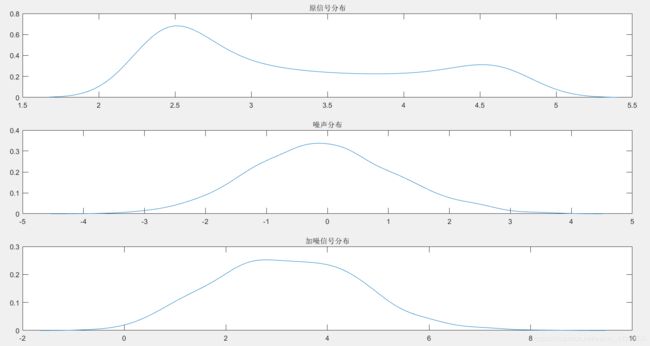
title('原信号分布')
[f2,xi2]=ksdensity(noise);
subplot(312)
plot(xi2,f2)
title('噪声分布')
[f3,xi3]=ksdensity(xn);
subplot(313)
plot(xi3,f3)
title('加噪信号分布')
结果图
参考资料
维纳滤波课件
广义平稳过程
维纳滤波与维纳-霍夫方程
维纳滤波的理论及应用
自相关函数是信号与延迟信号相似性的度量，延迟信号为0时，则称为信号的均方值，此时他的值最大。 ↩︎
最优指以估计结果与信号真值之间的误差的均方值最小为最佳准则。 ↩︎