数据结构

数据是信息的载体，是计算机程序加工的原料，数据元素是数据的基本单位，数据项是构成数据元素的最小单位。数据对象是具有相同性质的数据元素的集合（强调的是数据元素性质的相同）。

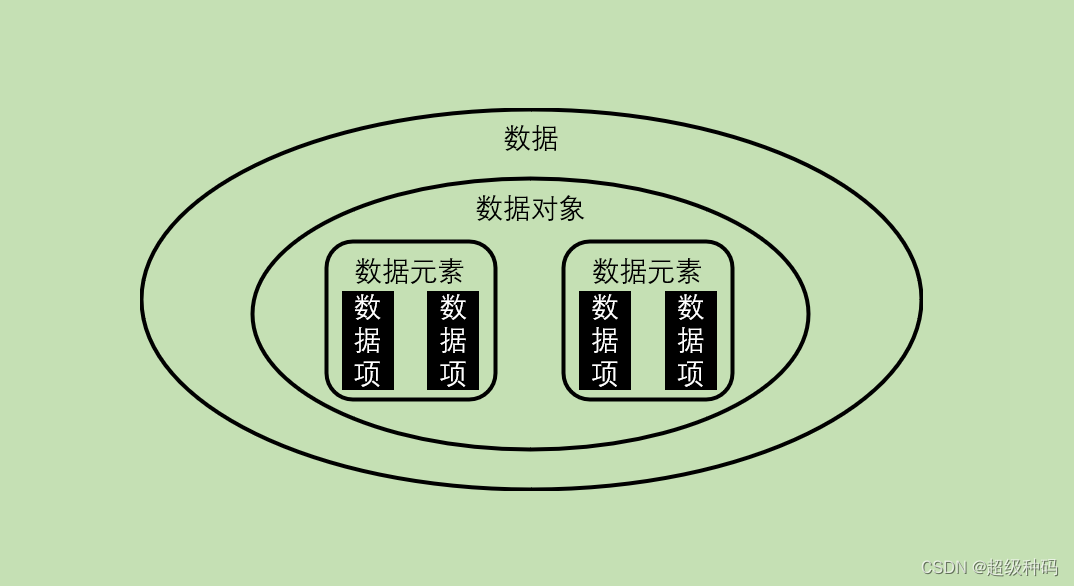
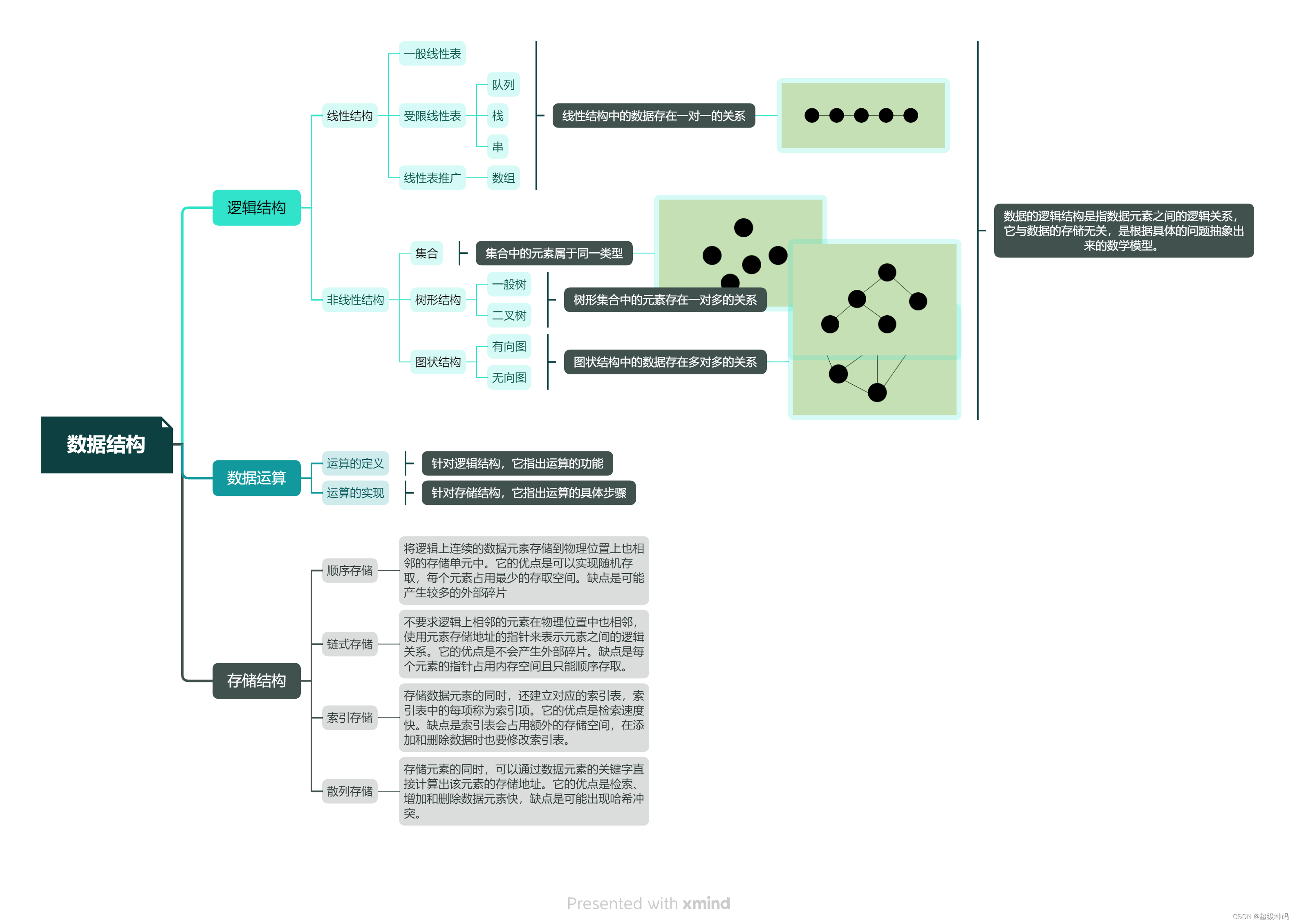
数据结构是指相互之间存在一种或多种特定关系的数据元素的集合（强调的是数据元素之间的关系）。数据结构的三要素是逻辑结构、存储结构和数据运算。

算法

算法是为求解一个问题需要遵循的、被清楚指定的简单指令的集合。一个算法具有以下五个特性：

一个算法的设计取决于所选定的逻辑结构，而算法的实现依赖于所采用的存储结构。

算法分析

一旦给定一个算法并且确认其是正确的，那么重要的一步就是对这个算法进行算法分析，算法分析主要考虑算法的效率，算法效率包含以下两方面：

• 时间效率：指算法所消耗的时间，用时间复杂度来表示。
• 空间效率：指算法执行过程中所消耗的存储空间。用空间复杂度来表示。

时间复杂度

一个算法的运行的时间大致可以等于计算机执行算法指令的时间（$t$）与指令执行次数（$n$）的乘积。
$$T(n)=\sum _{i=1}^n{t}_i\times n$$

由于每个指令执行的时间由计算机的硬件和软件条件决定，和算法本身没有关系，因此可以将每个指令执行的时间可以看作一个单位时间，那么讨论算法执行时间的问题就变成了讨论算法执行频度的问题：

$$T(n)=\sum _{i=1}^{n}n$$

下面分析一下选择排序算法的执行频度：

public static void selectionSort(int []data){for (int i = 0; i < data.length-1; i++) { //n次int minIndex=i; //n-1次for (int j = i+1; j < data.length; j++) { //n(n-1)/2次if (data[j]<data[minIndex]){ //n(n-2)/2次minIndex=j; //n(n-2)/2次}}int temp=data[i]; //n-1次data[i]=data[minIndex]; //n-1次data[minIndex]=temp; //n-1次}
}

所以选择排序的执行频度为：
$$T(n)=3n^2÷2+5n÷2-4$$

但是这一过程也相当的繁琐并且结果难以比较，由公式
$$\underset{x\to \infty }{\lim }\frac{a_n{x}^n+a_{n-1}{x}^{n-1}+\cdots +a_{1}x+a_0}{b_m{x}^m+b_{m-1}{x}^{m-1}+\cdots +b_{1}x+b_0}=\{\begin{array}{l}\frac{a_n}{b_m},n=m\\ 0,n<m\\ \infty ,n>m\end{array}$$
可知，如果存在一个函数$f(n)$，使$$\underset{n\to \infty }{\lim }\frac{T(n)}{f(n)}=C(C\ne 0)$$，那么$f(n)$和$T(n)$就是同阶的，记作$T(n)=O(f(n))$，$O(f(n))$就称为算法的时间复杂度。那么上述选择排序的时间复杂度就为$O(n^2)$。也就是说在寻找算法频度时不需要找出所有语句执行的频度，只需要找出对算法频度贡献最大的语句即可。此外，输入数据的性质会影响算法的执行频度，在这种情况下将算法的时间复杂度分为三种：

• 最坏时间复杂度：输入数据的性质使算法的执行频度很高。
• 平均时间复杂度：输入数据的性质使算法的执行频度很平均。
• 最好时间复杂度：输入数据的性质使算法的执行频度很低。

但一般只考虑最坏时间复杂度，以保证算法的运行时间不会比它更长。在计算程序的时间复杂度时，有以下两条规则：

• 加法原则：$T(n)=T_1(n)+T_2(n)=O(f(n))+O(g(n))=O(max(f(n),g(n)))$
• 乘法原则：$T(n)=T_1(n)\times T_2(n)=O(f(n))\times O(g(n))=O(f(n)\times Og(n))$

常见时间复杂度的关系为：
$$O(1)<O(lo{g}_{2}n)<O(n)<O(nlo{g}_{2}n)<O(n^2)<O(n^3)<O(2^n)<O(n!)<O(n^n)$$

空间复杂度

与时间复杂度类似，算法的空间复杂度记作：
$$S(n)=O(f(n))$$

它包括算法本身要占据的空间以及使用的辅助空间。在计算空间复杂度时只需要计算辅助空间即可，比如上述的选择排序算，它仅需要一个临时变量作为辅助空间，所以它的空间复杂度为$O(1)$，当算法的空间复杂度为$O(1)$时称它在原地工作。注意，当函数递归调用时，要考虑每一次递归使用的辅助空间。