前言
常见的需要求解的角有:异面直线所成的角,线面角,二面角,向量的夹角;
典例剖析
例1【2017凤翔中学高三第三次月考第10题】【异面直线所成的角】
长方体\(ABCD-A_1B_1C_1D_1\)中,\(AB=AA_1=2\),\(AD=1\),则异面直线\(BC_1\)与\(AC\)所成的角的余弦值是多少?
法1:立体几何法,作证算,思路:将两条异面直线平移至一个三角形中,然后解三角形得到。
将\(BC_1\)平移到\(AD_1\),联结\(CD_1\),则\(\angle CAD_1\)为两条异面直线所成的角,
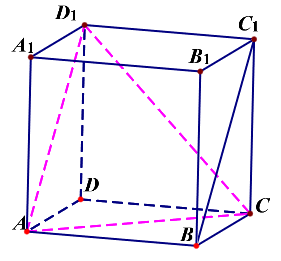
在\(\Delta ACD_1\)中,可知\(AC=\sqrt{5}\),\(AD_1=\sqrt{5}\),\(CD_1=2\sqrt{2}\),
由余弦定理可知\(cos\angle CAD_1=\cfrac{(\sqrt{5})^2+(\sqrt{5})^2-(2\sqrt{2})^2}{2\cdot \sqrt{5}\cdot \sqrt{5}}=\cfrac{1}{5}\);
法2:空间向量法,
以点\(D\)为坐标原点,分别以\(DA、DC、DD_1\)所在的直线为\(x、y、z\)轴建立如图所示的直角坐标系,
则点\(D(0,0,0)\),\(A(1,0,0)\),\(C(0,2,0)\),\(B(1,2,0)\),\(D_1(0,0,2)\),\(A_1(1,0,2)\),\(B_1(1,2,2)\),\(C_1(0,2,2)\),
故\(\overrightarrow{BC_1}=(-1,0,2)\),\(\overrightarrow{AC}=(-1,2,0)\),
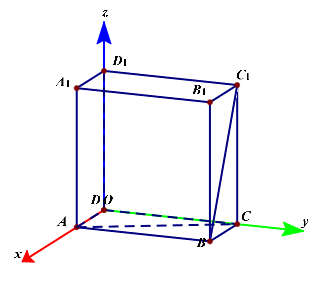
设两条异面直线所成的角为\(\theta\),则\(cos\theta=|cos<\overrightarrow{BC_1},\overrightarrow{AC}>|=\cfrac{(-1)\times(-1)+0\times2+2\times 0}{\sqrt{(-1)^2+0^2+2^2}\times\sqrt{(-1)^2+2^2+0^2}}=\cfrac{1}{5}\)。
备注:两条异面直线所成角的范围\([0,\cfrac{\pi}{2}]\),两个向量所成角的范围\([0,\pi]\)。
例2【2017凤翔中学第三次月考理科第19题】【二面角】
如图所示,四棱锥\(P-ABCD\)中,底面\(ABCD\)是个边长为2的正方形,侧棱\(PA\perp\)底面\(ABCD\),且\(PA=2\),\(Q\)是\(PA\)的中点.
(1)证明:\(BD\perp\)平面\(PAC\) ;
暂略
(2)求二面角\(C-BD-Q\)的余弦值。
分析:由题可知,\(AB、AP、AD\)两两垂直,以\(A\)为坐标原点,分别以\(AB、AD、AP\)所在直线为\(x,y,z\)轴建立空间直角坐标系,如图所示。

则点\(B(2,0,0)\),\(C(2,2,0)\),\(D(0,2,0)\),\(Q(0,0,1)\),
所以\(\overrightarrow{BD}=(-2,2,0)\),\(\overrightarrow{BQ}=(-2,0,1)\),
设平面\(BDQ\)的法向量为\(\vec{m}=(x,y,z)\),则有
\(\begin{cases}\vec{m}\perp\overrightarrow{BD}\\\vec{m}\perp\overrightarrow{BQ}\end{cases}\) \(\Longrightarrow \begin{cases}\vec{m}\cdot\overrightarrow{BD}=0\\\vec{m}\cdot\overrightarrow{BQ}=0\end{cases}\)
即\(\begin{cases}-2x+2y=0\\-2x+z=0\end{cases}\),可以取\(\vec{m}=(1,1,2)\)
平面\(BDC\)的法向量为\(\vec{n}=(0,0,1)\),
设二面角\(C-BD-Q\)为\(\theta\),由图可知,\(\theta\)为钝角,则有
\(cos\theta=-|cos<\vec{m},\vec{n}>|=-\cfrac{\vec{m}\cdot\vec{n}}{|\vec{m}||\vec{n}|}=-\cfrac{2}{\sqrt{6}}=-\cfrac{\sqrt{6}}{3}\)
所以二面角\(C-BD-Q\)的余弦值为\(-\cfrac{\sqrt{6}}{3}\)。
备注:二面角的范围\([0,\pi]\)。
例3【2019届高三理科数学三轮模拟试题】在长方体\(ABCD-A_1B_1C_1D_1\)中,已知直线\(BD\)与平面\(ADD_1A_1\)所成角的正切值为\(2\),直线\(BD_1\)与平面\(ABCD\)所成角的正弦值为\(\cfrac{2}{3}\),则异面直线\(CD_1\)与\(BD_1\)所成角的余弦值为【】
分析:如图所示,直线\(BD\)与平面\(ADD_1A_1\)所成角的为\(\angle BDA\),则由\(tan\angle BDA=2\),可以设\(AB=2k\),\(AD=k\),则\(BD=\sqrt{5}k\),直线\(BD_1\)与平面\(ABCD\)所成角的为\(\angle D_1BD\),则由\(sin\angle D_1BD=\cfrac{2}{3}\),可以设\(DD_1=2m\),\(BD_1=3m\),则\(BD=\sqrt{5}m\),
故可以令\(m=k=1\),则长方体的三维\(AB=2\),\(AD=1\),\(DD_1=2\),接下来的思路可以有两个:
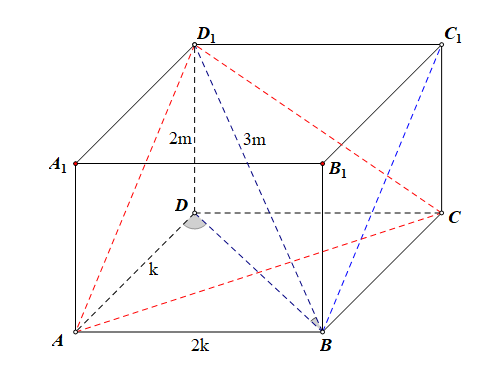
思路1:平移法,将异面直线\(CD_1\)与\(BD_1\)通过平移放置到同一个三角形\(\triangle AVD_1\)中,这样\(AC=\sqrt{5}\),\(AD_1=\sqrt{5}\),\(CD_1=2\sqrt{2}\),则异面直线\(CD_1\)与\(BD_1\)所成的角即为\(\angle AD_1C\),由余弦定理可知\(cos \angle AD_1C=\cfrac{\sqrt{10}}{5}\).
思路2:空间向量法,不作平移,直接利用直线的方向向量的夹角来求解;
