广度优先搜索应用举例:计算网络跳数
图结构在解决许多网络相关的问题时直到了重要的作用。
比如,用来确定在互联网中从一个结点到另一个结点(一个网络到其他网络的网关)的最佳路径。一种建模方法是采用无向图,其中顶点表示网络结点,边代表结点之间的联接。使用这种模型,可以采用广度优先搜索来帮助确定结点间的最小跳数。
如图1所示,该图代表Internet中的6个网络结点。以node1作为起点,有不止1条可以通往node4的路径。<node1,node2,node4>,<node1,node3,node2,node4>,<node1,node3,node5,node4>都是可行的路径。广度优先搜索可以确定最短路径选择,即<node1,node2,node4>,一共只需要两跳。

我们以bfs作为广度优先搜索的函数名(见示例1及示例2)。该函数用来确定互联网中两个结点之间的最小跳数。这个函数有3个参数:graph是一个图,在这个问题中就代表整个网络;start代表起始的顶点;hops是返回的跳数链表。函数bfs会修改图graph,因此,如果有必要的话在调用该函数前先对图创建拷贝。另外,hops中返回的是指向graph中实际顶点的指针,因此调用者必须保证只要访问hops,graph中的存储空间就必须保持有效。
graph中的每一个顶点都是一个BfsVertex类型的结构体(见示例1),该结构体有3个成员:data是指向图中顶点的数据域指针,color在搜索过程中维护顶点的颜色,hops维护从起始顶点开始到目标顶点的跳数统计。
match函数是由调用者在初始化graph时作为参数传递给graph_init的。match函数应该只对BfsVertex结构体中的data成员进行比较。
bfs函数将按照前面介绍过的广度优先搜索的方式来计算。为了记录到达每个顶点的最小跳数,将每个顶点的hop计数设置为与该顶点邻接的顶点的hop计数加1。对于每个发现的顶点都这样处理,并将其涂成灰色。每个顶点的颜色和跳数信息都由邻接表结构链表中的BfsVertex来维护。最后,加载hops中所有跳数未被标记为-1的顶点。这些就是从起始顶点可达的顶点。
bfs的时间复杂度为O(V+E),这里V代表图中的顶点个数,E是边的个数。这是因为初始化顶点的颜色属性以及确保起始顶点存在都需要O(V)的运行时间,广度优先搜索中的循环的复杂度是O(V+E),加载跳数统计链表的时间为O(V)。
示例1:广度优先搜索的头文件
/*bfs.h*/ #ifndef BFS_H #define BFS_H#include "graph.h" #include "list.h"/*定义广度优先搜索中的顶点数据结构*/ typedef struct BfsVertex_ {void *data;VertexColor color;int hops; }BfsVertex;/*函数接口定义*/ int bfs(Graph *graph, BfsVertex *start, List *hops);#endif // BFS_H
示例2:广度优先搜索的实现
/*bfs.c*/ #include <stdlib.h> #include "bfs.h" #include "graph.h" #include "list.h" #include "queue.h"/*bfs */ int bfs(Graph *graph, BfsVertex *start, List *hops) {Queue queue;AdjList *adjlist, *clr_adjlist;BfsVertex *clr_vertex, *adj_vertex;ListElmt *element, *member;/*初始化图中的所有结点为广度优先结点*/for(element = list_head(&graph_adjlists(graph)); element != NULL; element = list_next(element)){clr_vertex = ((AdjList *)list_data(element))->vertex;if(graph->match(clr_vertex,start)){/*初始化起始顶点*/clr_vertex->color = gray;clr_vertex->hops = 0;}else{/*初始化非起始顶点*/clr_vertex->color = white;clr_vertex->hops = -1;}}/*初始化队列,并将起始顶点的邻接表入队*/queue_init(&queue,NULL);/*返回起始顶点的邻接表,存储到clr_adjlist*/if(graph_adjlist(graph,start,&clr_adjlist) != 0){queue_destroy(&queue);return -1;}/*将顶点的邻接表入队到队列*/if(queue_enqueue(&queue,clr_adjlist) != 0 ){queue_destroy(&queue);return -1;}/*执行广度优先探索*/while(queue_size(&queue) > 0){adjlist = queue_peek(&queue);/*遍历邻接表中的每一个顶点*/for(member = list_head(&adjlist->adjacent); member != NULL; member = list_next(member)){adj_vertex = list_data(member);/*决定下一个邻接点的颜色*/if(graph_adjlist(graph,adj_vertex,&clr_adjlist) != 0){queue_destroy(&queue);return -1;}clr_vertex = clr_adjlist->vertex;/*把白色的顶点标成灰色,并把它的邻接顶点入队*/if(clr_vertex->color == white){clr_vertex->color = gray;clr_vertex->hops = ((BfsVertex *)adjlist->vertex)->hops + 1;if(queue_enqueue(&queue,clr_adjlist) != 0){queue_destroy(&queue);return -1;}}}/*将当前顶点邻接表从队列中移除并涂成黑色*/if(queue_dequeue(&queue,(void **)&adjlist) == 0){((BfsVertex *)adjlist->vertex)->color = black;}else{queue_destroy(&queue);return -1;}}queue_destroy(&queue);/*返回每一个顶点的hop计数到一个链表中*/list_init(hops,NULL);for(element = list_head(&graph_adjlists(graph)); element != NULL; element = list_next(element)){/*跳过那些没有被访问到的节点(hops = -1)*/clr_vertex = ((AdjList *)list_data(element))->vertex;if(clr_vertex->color != -1){if(list_ins_next(hops,list_tail(hops),clr_vertex) != 0){list_destroy(hops);return -1;}}}return 0; }
深度优先搜索的应用举例:拓扑排序
有时候,我们必须根据各种事物间的依赖关系来确定一种可接受的执行顺序。比如,在大学里必须满足一些先决条件才能选的课程,或者一个复杂的项目,其中某个特定的阶段必须在其他阶段开始之前完成。要为这一类问题建模,可以采用优先级图,其采用的是有向图的思路。在优先级图中,顶点代表任务,而边代表任务之间的依赖关系。以必须先完成的任务为起点,以依赖于此任务的其他任务为终点,画一条边即可。
如下图所示,它表示7门课程及其先决条件组成的一份课程表:S100没有先决条件,S200需要S100,S300需要S200和M100,M100没有先决条件,M200需要M100,M300需要S300和M200,并且S150没有先决条件同时也不是先决条件。
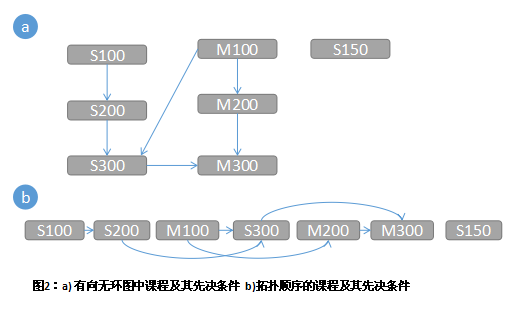
通过对这些课程执行拓扑排序,深度优先搜索有助于确定出一中可接受的顺序。
拓扑排序将顶点排列为有向无环图,因此所有的边都是从左到右的方向。正规来说,有向无环图G=(V,E)的拓扑排序是其顶点的一个线性排序,以便如果G中存在一条边(u,v),那么线性顺序中u出现在v的前面,在许多情况下,满足此条件的顺序有多个。
下面的代码示例实现了函数dfs,即深度优先搜索。该函数在这里用来对任务做拓扑排序。dfs有两个参数:graph代表图,在这个问题中则代表需要排序的任务;而参数ordered是完成拓扑排序后返回的顶点链表。调用该函数会修改图graph,因此如果有必要需要在调用前先对graph创建一个副本。另外,函数返回后链表ordered中保存了指向图graph中顶点的指针,因此调用者必须保证,一旦访问ordered中的元素就必须保证graph中的存储空间保持有效。graph中的每一个顶点都是一个DfsVertex结构体,该结构体拥有两个成员:data是指向顶点数据域部分的指针;而color在搜索过程中负责维护顶点的颜色信息。match函数是由调用者在初始化graph时通过参数传递给graph_init的,该函数应该只对DfsVertex结构体中的data成员进行比较。
dfs按照深度优先的方式进行搜索。dfs_main是实际执行搜索的函数。dfs中的最后一个循环保证对图中所有未相连的元素完成了检索。在dfs_main中逐个完成顶点的搜索并将其涂黑,然后插入链表ordered的头部。最后,ordered就包含完整拓扑排序后的顶点。
dfs的时间复杂度是O(V+E),V代表图中的顶点个数,而E代表边的个数。这是因为初始化顶点的颜色信息需要O(V)的时间,而dfs_main的时间复杂度为O(V+E)。
示例3:深度优先搜索的头文件
/*dfs.h*/ #ifndef DFS_H #define DFS_H#include "graph.h" #include "list.h"/*为深度优先搜索中的所有节点定义一个结构体*/ typedef struct DfsVertex_ {void *data;VertexColor color; }DfsVertex;/*公共接口*/ int dfs(Graph *graph,List *ordered);#endif // DFS_H
示例4:深度优先搜索的函数实现
/*dfs.c*/ #include <stdlib.h>#include "dfs.h" #include "graph.h" #include "list.h"/*dfs_main*/ static int dfs_main(Graph *graph, AdjList *adjlist, List *ordered) {AdjList *clr_adjlist;DfsVertex *clr_vertex, *adj_vertex;ListElmt *member;/*首先,将起始顶点涂成灰色,并遍历它的邻接顶点集合*/((DfsVertex *)adjlist->vertex)->color = gray;for(member = list_head(&adjlist->adjacent); member != NULL; member = list_next(member)){/*决定下一个集合顶点的颜色*/adj_vertex = list_data(member);if(graph_adjlist(graph,adj_vertex,&clr_adjlist) != 0){return -1;}clr_vertex = clr_adjlist->vertex;/*如果当前顶点是白色,则递归搜索它的邻接点*/if(clr_vertex->color == white){if(dfs_main(graph,clr_adjlist,ordered) != 0)return -1;}}/*把当前顶点涂成“黑”色,并加入到链表头部*/((DfsVertex *)adjlist->vertex)->color = black;if(list_ins_next(ordered, NULL, (DfsVertex *)adjlist->vertex) !=0 )return -1;return 0; }/*dfs*/ int dfs(Graph *graph, List *ordered) {DfsVertex *vertex;ListElmt *element;/*初始化图中的所有顶点*/for(element = list_head(&graph_adjlists(graph)); element != NULL; element = list_next(element)){vertex = ((AdjList *)list_data(element))->vertex;vertex->color = white;}/*执行广度优先搜索*/list_init(ordered,NULL);for(element = list_head(&graph_adjlists(graph)); element != NULL; element = list_next(element)){/*确保图中的每个顶点都能被检索到*/vertex = ((AdjList *)list_data(element))->vertex;if(vertex->color == white){if(dfs_main(graph, (AdjList *)list_data(element), ordered) != 0){list_destroy(ordered);return -1;}}}return 0; }
