当前位置：首页 > news >正文

销售网站建设/黄冈免费网站推广平台汇总

news 2025/8/12 12:04:51

销售网站建设,黄冈免费网站推广平台汇总,温州龙湾区企业网站搭建价格,网站建设广西迷宫问题(MazePath)的求解——利用回溯法(backtracking) 1. 迷宫问题的提法迷宫问题是典型的图的搜索问题。假设一个迷宫，只有一个入口和一个出口。如果从迷宫的入口到达出口，途中不出现行进方向错误，则得到一条最佳路线。为此&#xff0c…

迷宫问题(MazePath)的求解——利用回溯法(backtracking)

1. 迷宫问题的提法

迷宫问题是典型的图的搜索问题。
假设一个迷宫，只有一个入口和一个出口。如果从迷宫的入口到达出口，途中不出现行进方向错误，则得到一条最佳路线。
为此，用一个二维数组maze[m][n]来表示迷宫。
(1)当数组元素maze[i][j]=1 (0≤i≤m-1,1≤j≤n-1)，表示该位置是墙壁，不能通行。
(2)当数组元素maze[i][j]=0 (0≤i≤m-1,1≤j≤n-1)，表示该位置是通路，可以通行。
注：数组的第0行、第m-1行，第0列、第n-1列，必须是迷宫的围墙，即上述行列的所有坐标对应的数值必须为1(除了入口和出口两个位置的坐标对应的数值可以为0以外)，不能通行。

2. 回溯法的概念

2.1 回溯法的定义

回溯法(backtracking)是一种选优搜索法，又称为试探法，按选优条件向前搜索，以达到目标。

2.2 回溯法的思想

回溯法将问题的候选解按某种顺序逐一枚举和检验。
(1)当发现当前的候选解不可能是解时，就放弃它而选择下一个候选解。
(2)如果当前的候选解除了不满足问题规模要求外，其他所有要求都已满足，则扩大当前候选解的规模继续试探。
(3)如果当前的候选解满足了包括问题规模在内的所有要求，则这个候选解将成为问题的一个解。
注：
(1)当探索到某一步时，发现原先选择并不优或达不到目标，就退回一步重新选择，这种走不通就退回再走的技术为回溯法，而满足回溯条件的某个状态的点称为“回溯点”。
(2)扩大当前候选解的规模并继续试探的过程叫做向前试探。
(3)用回溯法求解问题时常常使用递归方法进行试探，或使用栈帮助向前试探和回溯。

3. 用回溯法求解迷宫问题的算法原理

在求解迷宫问题的过程中，当沿某一条路径一步步走向出口但发现进入死胡同走不通时，就回溯一步或多步，寻找其他可走的路径，这就是回溯。
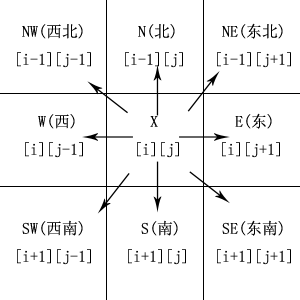
设任一时刻在迷宫中的位置[i][j]标记为X，X周围有8个前进方向，它实际是一系列交通路口，如果某一方向是0值，表示该方向有路可通，反之表示该方向已堵死。
为了有效地选择下一位置，可以将从位置[i][j]出发可能的前进方向预先定义在一个表内，按顺时针方向为N([i-1][j])，NE([i-1][j+1])，E([i][j+1])，SE([i+1][j+1])，S([i+1][j])，SW([i+1][j-1])，W([i][j-1])，NW([i-1][j-1])。
(1)前进方向示意图：

(2)前进方向表：

Move[q].dir move[q].a move[q].b
“N” -1 0
“NE” -1 1
“E” 0 1
“SE” 1 1
“S” 1 0
“SW” 1 -1
“W” 0 -1
“NW” -1 -1

Move[q].dir	move[q].a	move[q].b
“N”	-1	0
“NE”	-1	1
“E”	0	1
“SE”	1	1
“S”	1	0
“SW”	1	-1
“W”	0	-1
“NW”	-1	-1

4. 利用递归求解迷宫问题

4.1 迷宫的初始化及前进方向表的定义

文件：MazeConfig.h


#pragma once#include <iostream>#include <windows.h>using namespace std;//位置坐标和前进方向序号的三元组结构定义
struct items
{int x;//位置的x坐标int y;//位置的y坐标int dir;//前进方向的序号
};//前进方向表的结构定义
struct offfsets
{int a;//x方向的偏移int b;//y方向的偏移char *dir;//移动的方向描述
};const int m = 14;//迷宫的行数
const int n = 17;//迷宫的列数
const int dir_count = 8;//前进方向的总数
const int pathmark = 6;//迷宫通路的标识值static int mark[m][n];//访问标记数组items entry = { 1, 0, 0 };//迷宫入口网格坐标
items exitus = { m - 2, n - 1, 0 };//迷宫出口网格坐标//各个方向的偏移表定义
offfsets moves[dir_count] =
{{ -1, 0, "N" },{ -1, 1, "NE" },{ 0, 1, "E" },{ 1, 1, "SE" },{ 1, 0, "S" },{ 1, -1, "SW" },{ 0, -1, "W" },{ -1, -1, "NW" }
};//初始化迷宫
int Maze[m][n] =
{{ 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1 },{ 0, 0, 1, 0, 0, 0, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1 },{ 1, 1, 0, 0, 0, 1, 1, 0, 1, 1, 1, 0, 0, 1, 1, 1, 1 },{ 1, 0, 1, 1, 0, 0, 0, 0, 1, 1, 1, 1, 0, 0, 1, 1, 1 },{ 1, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 0, 1, 1, 0, 0, 1 },{ 1, 1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1 },{ 1, 0, 0, 1, 1, 0, 1, 1, 1, 0, 1, 0, 0, 1, 0, 1, 1 },{ 1, 0, 0, 1, 1, 0, 1, 1, 1, 0, 1, 0, 0, 1, 0, 1, 1 },{ 1, 0, 1, 1, 1, 1, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1 },{ 1, 0, 0, 1, 1, 0, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1 },{ 1, 1, 1, 0, 0, 0, 1, 1, 0, 1, 1, 0, 0, 0, 0, 0, 1 },{ 1, 0, 0, 1, 1, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 0, 1 },{ 1, 0, 1, 0, 0, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 0, 0 },{ 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1 }
};//初始化访问标记数组
void init_mark()
{for (int i = 0; i < m; i++){for (int j = 0; j < n; j++){mark[i][j] = 0;}}
}//打印迷宫
void print_maze()
{cout << "======>MazePath" << endl;for (int i = 0; i < m; i++){for (int j = 0; j < n; j++){if (Maze[i][j] == pathmark){SetConsoleTextAttribute(GetStdHandle(STD_OUTPUT_HANDLE), FOREGROUND_INTENSITY | FOREGROUND_GREEN);}else{SetConsoleTextAttribute(GetStdHandle(STD_OUTPUT_HANDLE), FOREGROUND_INTENSITY);}cout << Maze[i][j] << " ";}cout << endl;}SetConsoleTextAttribute(GetStdHandle(STD_OUTPUT_HANDLE), FOREGROUND_INTENSITY);
}

4.2 迷宫问题的递归求解算法实现

文件：SeekPath.h


#pragma once#include "MazeConfig.h"//从迷宫入口[entry.x][entry.y]开始，寻找通向出口的一条路径。
//如果找到，则函数返回true。
//如果没找到，则函数返回false。
bool SeekPath(items tmp)
{   if ((tmp.x == exitus.x) && (tmp.y == exitus.y)){SetConsoleTextAttribute(GetStdHandle(STD_OUTPUT_HANDLE), FOREGROUND_INTENSITY | FOREGROUND_GREEN);cout << "======>SeekPath Success" << endl;return true;//已到达出口，函数返回1。}items next;//下一个网格的位置for (int d = 0; d < dir_count; d++)//依次按每一个方向寻找通向出口的路径{next.x = tmp.x + moves[d].a;next.y = tmp.y + moves[d].b;if ((Maze[next.x][next.y] == 0) && (mark[next.x][next.y] == 0)){//下一位置可通，试探该方向mark[next.x][next.y] = 1;//标记为已访问过if (SeekPath(next) == true)//从此位置递归试探{//cout << "(" << nextGrid.x << "," << nextGrid.y << ")," << "Direction:" << moveTable[i].dir << ", ";Maze[next.x][next.y] = pathmark;return true;//试探成功，逆向输出路径坐标}}//回溯，换一个方向再试探通向出口的路径。}if ((tmp.x == entry.x) && (tmp.y == entry.y)){SetConsoleTextAttribute(GetStdHandle(STD_OUTPUT_HANDLE), FOREGROUND_INTENSITY | FOREGROUND_RED);cout << "======>SeekPath Fail" << endl;}return false;//无可通路到出口，函数返回0。
}

4.3 主函数(main函数)的实现

文件：main.cpp


#include "SeekPath.h"int main()
{init_mark();print_maze();if (SeekPath(entry) == true){//cout << "(" << entry.x << "," << entry.y << ")" << endl;Maze[entry.x][entry.y] = pathmark;  }print_maze();system("pause");return 0;
}

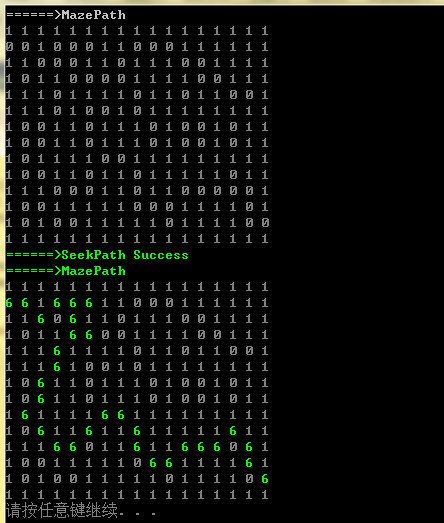
4.4 迷宫问题求解结果

控制台输出，迷宫通路是绿色高亮显示的路径。

5. 利用栈求解迷宫问题

5.1 链式栈的类定义及其操作的实现

文件：LinkedStack.h


#ifndef LINKED_STACK_H_#define LINKED_STACK_H_#include <iostream>using namespace std;template <class T>
struct LinkNode         //链表结点类的定义
{T data;             //数据域LinkNode<T> *link;  //指针域——后继指针//仅初始化指针成员的构造函数LinkNode(LinkNode<T>* ptr = NULL){ link = ptr; }//初始化数据与指针成员的构造函数LinkNode(const T& value, LinkNode<T>* ptr = NULL){ data = value; link = ptr; }
};template <class T>
class LinkedStack
{
public:LinkedStack();                      //构造函数~LinkedStack();                     //析构函数
public:void Push(const T& x) ;         //新元素x进栈bool Pop(T& x);                 //栈顶元素出栈，并将该元素的值保存至xLinkNode<T>* getTop() const;    //获取栈顶结点bool IsEmpty() const;           //判断栈是否为空void MakeEmpty();               //清空栈的内容
private:LinkNode<T> *top;   //栈顶指针，即链头指针
};//构造函数
template <class T>
LinkedStack<T>::LinkedStack()
: top(NULL)
{cout << "$ 执行构造函数" << endl;
}                       //析构函数
template <class T>
LinkedStack<T>::~LinkedStack()
{cout << "$ 执行析构函数" << endl;MakeEmpty();
}   //新元素x进栈
template <class T>
void LinkedStack<T>::Push(const T& x)
{LinkNode<T> *newNode = new LinkNode<T>(x);newNode->link = top;top = newNode;
}//栈顶元素出栈，并将该元素的值保存至x
template <class T>
bool LinkedStack<T>::Pop(T& x)
{if (true == IsEmpty()){return false;}LinkNode<T> *curNode = top;top = top->link;x = curNode->data;delete curNode;return true;
}//获取栈顶结点
template <class T>
LinkNode<T>* LinkedStack<T>::getTop() const
{return top;
}//判断栈是否为空
template <class T>
bool LinkedStack<T>::IsEmpty() const
{return (NULL == top) ? true : false;
}//清空栈的内容
template <class T>
void LinkedStack<T>::MakeEmpty()
{LinkNode<T> *curNode = NULL;while (NULL != top)             //当链表不为空时，删去链表中所有结点{curNode = top;              //保存被删结点top = curNode->link;        //被删结点的下一个结点成为头结点delete curNode;             //从链表上摘下被删结点}
}#endif /* LINKED_STACK_H_ */

5.2 迷宫的初始化及前进方向表的定义

文件：MazeConfig.h


#ifndef MAZECONFIG_H_#define MAZECONFIG_H_#include <iostream>#include <windows.h>using namespace std;//位置坐标和前进方向序号的三元组结构定义
struct items
{int x;//位置的x坐标int y;//位置的y坐标int dir;//前进方向的序号
};//前进方向表的结构定义
struct offfsets
{int a;//x方向的偏移int b;//y方向的偏移char *dir;//移动的方向描述
};const int m = 14;//迷宫的行数
const int n = 17;//迷宫的列数
const int dir_count = 8;//前进方向的总数
const int pathmark = 6;//迷宫通路的标识值static int mark[m][n];//访问标记数组items entry = { 1, 0, 0 };//迷宫入口网格坐标
items exitus = { m - 2, n - 1, 0 };//迷宫出口网格坐标//各个方向的偏移表定义
offfsets moves[dir_count] =
{{ -1, 0, "N" },{ -1, 1, "NE" },{ 0, 1, "E" },{ 1, 1, "SE" },{ 1, 0, "S" },{ 1, -1, "SW" },{ 0, -1, "W" },{ -1, -1, "NW" }
};//初始化迷宫
int Maze[m][n] =
{{ 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1 },{ 0, 0, 1, 0, 0, 0, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1 },{ 1, 1, 0, 0, 0, 1, 1, 0, 1, 1, 1, 0, 0, 1, 1, 1, 1 },{ 1, 0, 1, 1, 0, 0, 0, 0, 1, 1, 1, 1, 0, 0, 1, 1, 1 },{ 1, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 0, 1, 1, 0, 0, 1 },{ 1, 1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1 },{ 1, 0, 0, 1, 1, 0, 1, 1, 1, 0, 1, 0, 0, 1, 0, 1, 1 },{ 1, 0, 0, 1, 1, 0, 1, 1, 1, 0, 1, 0, 0, 1, 0, 1, 1 },{ 1, 0, 1, 1, 1, 1, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1 },{ 1, 0, 0, 1, 1, 0, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1 },{ 1, 1, 1, 0, 0, 0, 1, 1, 0, 1, 1, 0, 0, 0, 0, 0, 1 },{ 1, 0, 0, 1, 1, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 0, 1 },{ 1, 0, 1, 0, 0, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 0, 0 },{ 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1 }
};//初始化访问标记数组
void init_mark()
{for (int i = 0; i < m; i++){for (int j = 0; j < n; j++){mark[i][j] = 0;}}
}//打印迷宫
void print_maze()
{cout << "======>MazePath" << endl;for (int i = 0; i < m; i++){for (int j = 0; j < n; j++){if (Maze[i][j] == pathmark){SetConsoleTextAttribute(GetStdHandle(STD_OUTPUT_HANDLE), FOREGROUND_INTENSITY | FOREGROUND_GREEN);}else{SetConsoleTextAttribute(GetStdHandle(STD_OUTPUT_HANDLE), FOREGROUND_INTENSITY);}cout << Maze[i][j] << " ";}cout << endl;}SetConsoleTextAttribute(GetStdHandle(STD_OUTPUT_HANDLE), FOREGROUND_INTENSITY);
}#endif /* MAZECONFIG_H_ */

5.3 迷宫问题的非递归求解算法实现

文件：SeekPath.h


#ifndef SEEKPATH_H_#define SEEKPATH_H_#include "MazeConfig.h"#include "LinkedStack.h"template <class T>
void MarkPath(LinkedStack<T>* linkedStack)
{LinkNode<T> *curNode = linkedStack->getTop();while (NULL != curNode){items item = curNode->data;Maze[item.x][item.y] = pathmark;curNode = curNode->link;}
}//从迷宫入口[entry.x][entry.y]开始，寻找通向出口[m][p]的一条路径。
bool SeekPath()
{   init_mark();LinkedStack<items> *linkedStack = new LinkedStack<items>;   //设置工作栈items tmp = entry;  //初始化坐标方向为入口items cur, next;linkedStack->Push(tmp); //初始化的坐标方向三元组进栈while (linkedStack->IsEmpty() == false) //栈不为空时，继续进行搜索{linkedStack->Pop(tmp);  //退栈cur.x = tmp.x; cur.y = tmp.y; cur.dir = tmp.dir;    //当前位置坐标和下一个前进方向的序号while (cur.dir < dir_count) //还有移动，继续移动{next.x = cur.x + moves[cur.dir].a; next.y = cur.y + moves[cur.dir].b; next.dir = 0; //找下一个位置的坐标if ((next.x == exitus.x) && (next.y == exitus.y))   //到达出口{SetConsoleTextAttribute(GetStdHandle(STD_OUTPUT_HANDLE), FOREGROUND_INTENSITY | FOREGROUND_GREEN);cout << "======>SeekPath Success" << endl;linkedStack->Push(cur);linkedStack->Push(exitus);MarkPath(linkedStack);delete linkedStack;return true;}if ((Maze[next.x][next.y] == 0) && (mark[next.x][next.y] == 0)){mark[next.x][next.y] = 1;//标记为已访问过tmp.x = cur.x; tmp.y = cur.y; tmp.dir = cur.dir;    //记忆已通过位置和前进方向linkedStack->Push(tmp); //进栈cur.x = next.x; cur.y = next.y; cur.dir = next.dir; //移动到下一个网格，在各个方向试探}else{cur.dir++;  //试探下一个方向}}}SetConsoleTextAttribute(GetStdHandle(STD_OUTPUT_HANDLE), FOREGROUND_INTENSITY | FOREGROUND_RED);cout << "======>SeekPath Fail" << endl;delete linkedStack;return false;
}#endif /* SEEKPATH_H_ */

5.4 主函数(main函数)的实现

文件：main.cpp


#include "SeekPath.h"int main(int argc, char* argv[])
{print_maze();SeekPath();print_maze();   system("pause");return 0;
}

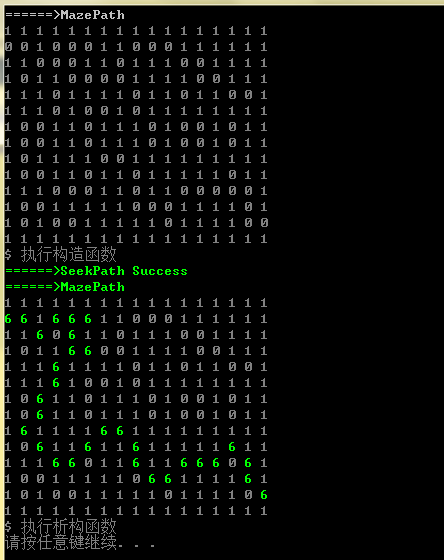
5.5 迷宫问题求解结果

控制台输出，迷宫通路是绿色高亮显示的路径。

参考文献：
[1]《数据结构(用面向对象方法与C++语言描述)(第2版)》殷人昆——第三章
[2] 百度搜索关键字：迷宫问题、回溯法、试探法

查看全文

http://www.lbrq.cn/news/1339129.html

移动手机号码网站/网络营销包括

飞沐网站建设公司北京/百度指数搜索指数的数据来源

iis网站找不到网页/东莞百度seo

那片海dede织梦源码企业网络公司工作室网站模板源码模板php/百度网页打不开

越烽建设集团有限公司网站/搜客通

都用什么软件做网站/怎么知道自己的域名

全网网站建设优化/新疆头条今日头条新闻

2017政府网站设计方案/百度网址大全旧版本

哪个网站反盗版做的最好/百度下载2021新版安装

在线购物网站建设流程图/电商中seo是什么意思

企业微信邮箱怎么开通注册/网站优化seo教程

哪些网站是用php开发的/广州网站优化

热烈祝贺公司网站上线/关键词排名是由什么决定的

wordpress ajax评论/长沙seo优化推广公司

财务公司管理系统/惠州seo排名

什么网站可以做拍a发布会/色盲和色弱的区别

景安网站上传完还要怎么做/长沙企业关键词优化哪家好

兰州网站建设公司/视频网站搭建

网站建设时间安排/seo搜索引擎优化工资多少钱

亚马逊广告底层逻辑重构：从流量博弈到价值创造的战略升维

机器翻译：一文掌握序列到序列（Seq2Seq）模型（包括手写Seq2Seq模型）

什么情况下会导致日本服务器变慢？解决办法

【测试报告】SoundWave（Java+Selenium+Jmeter自动化测试）

TC39x STM(System Timer)学习记录

人工智能-python-机器学习-决策树与集成学习：决策树分类与随机森林