做自己的网站流量怎么/网站建设流程图

1、什么是树

在数据结构中，树的定义如下：
树（tree）是 n（n≥0）个节点的有限集，当n=0时，称为空树，在任意一个非 空树中，有如下特点：

• 有且仅有一个特定的称为根的节点；
• 当n>1时，其余节点可分为m（m>0）个互不相交的有限集，每一个集合本身又是一个树，并称为根的子树
  下面这张图，就是一个标准的树结构：
  
  在上图中，节点1是根节点（root）；节点5、6、7、8是树的末端，没有孩子，被称为叶子节点（leaf）；图中的虚线部分，是根节点1的其中一个子树，同时，树的结构从根节点到叶子节点，分为不同的层级；从一个节点的角度来看，它的上下级和同级节点关系如下：
  
  在上图中，节点4的上一级节点，是节点4的父节点（parent）；从节点4衍生出 来的节点，是节点4的孩子节点（child）；和节点4同级，由同一个父节点衍生出来 的节点，是节点4的兄弟节点（sibling）；树的最大层级数，被称为树的高度或深度。【上图这个树的高度是4】

2、什么是二叉树

二叉树（binary tree）是树的一种特殊形式；顾名思义，这种树的每 个节点最多有2个孩子节点【这里是最多有2个，也可能只有1个，或者没有孩子节点】二叉树的结构如图所示：

二叉树节点的两个孩子节点，一个被称为左孩子（left child），一个被称为右孩子（right child）；
这两个孩子节点的顺序是固定的，就像人的左手就是左手，右手就是右手，不能够颠倒或混淆，此外，二叉树还有两种特殊形式，一个叫作满二叉树，另一个叫作完全二叉树！

满二叉树

一个二叉树的所有非叶子节点都存在左右孩子，并且所有叶子节点都在同一层 级上，那么这个树就是满二叉树，如下图：【满二叉树的每一个分支都是满的】

完全二叉树

对一个有n个节点的二叉树，按层级顺序编号，则所有节点的编号为从1到n；如果这个树所有节点和同样深度的满二叉树的编号为从1到n的节点位置相同，则这个二叉树为完全二叉树，如下图：

在上图中，二叉树编号从1到12的12个节点，和前面满二叉树编号从1到12的节点位置完全对应，因此这个树是完全二叉树；完全二叉树的条件没有满二叉树那么苛刻：满二叉树要求所有分支都是满的； 而完全二叉树只需保证最后一个节点之前的节点都齐全即可。

二叉树的物理存储结构

链式存储结构

链式存储是二叉树最直观的存储方式，如下图：

一个节点最多可以指向左右两个孩子节点，所以二叉树的每一个节点包含3部分：

• 存储数据的data变量
• 指向左孩子的left指针
• 指向右孩子的right指针

数组存储结构

使用数组存储时，会按照层级顺序把二叉树的节点放到数组中对应的位置上； 如果某一个节点的左孩子或右孩子空缺，则数组的相应位置也空出来

这样可以更方便地在数组中定位二叉树的孩子节点和父节点；假设一个父节点的下标是parent，那么它的左孩子节点下标就是2×parent + 1；右孩子节点下标就是2×parent + 2；反过来，假设一个左孩子节点的下标是leftChild，那么它的父节点下标就是 （leftChild-1）/ 2；
假如节点4在数组中的下标是3，节点4是节点2的左孩子，节点2的下标可以直接通过计算得出：

节点2的下标 = (3-1)/2 = 1

显然，对于一个稀疏的二叉树来说，用数组表示法是非常浪费空间的

3、二叉树的应用

二叉树包含许多特殊的形式，每一种形式都有自己的作用，但是其最主要的应用还在于进行查找操作和维持相对顺序这两个方面

【1】查找

二叉树的树形结构使它很适合扮演索引的角色：二叉查找树（binary search tree），这种二叉树的主要作用就是进行查找操作；二叉查找树在二叉树的基础上增加了以下几个条件：

• 如果左子树不为空，则左子树上所有节点的值均小于根节点的值
• 如果右子树不为空，则右子树上所有节点的值均大于根节点的值
• 左、右子树也都是二叉查找树

下图就是一个标准的二叉查找树：

例如查找值为4的节点，步骤如下：

• 1、访问根节点6，发现4<6；
  
• 2、访问节点6的左孩子节点3，发现4>3；
  
• 3、访问节点3的右孩子节点4，发现4=4，这正是要查找的节点
  
  对于一个节点分布相对均衡的二叉查找树来说，如果节点总数是n，那么搜索节点的时间复杂度就是O(logn)，和树的深度是一样的。

【2】 维持相对顺序

二叉查找树要求左子树小于父节点，右子树大于父节点，正是这样保证了二叉树的有序性；新插入的节点，同样要遵循二叉排序树的原则；例如插入新元素5，由于5<6， 5>3，5>4，所以5最终会插入到节点4的右孩子位置。

再如插入新元素10，由于10>6，10>8，10>9，所以10最终会插入到节点9的右孩子位置

这一切看起来很顺利，然而却隐藏着一个致命的问题；试着在二叉查找树中依次插入9、8、7、6、5、4，结果如下：

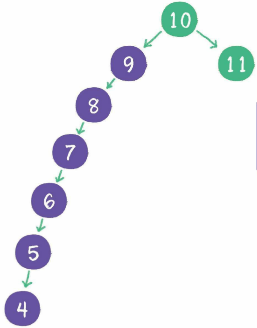
要解决这个问题就要涉及二叉树的自平衡，二叉树自平衡的方式有多种：如红黑树、AVL树、树堆等
—————————————————————————————————————————————
内容来源：《漫画算法》