试玩网站建设/免费搜索引擎入口

修改数组

题目来源：修改数组 - 蓝桥云课 (lanqiao.cn)

分析

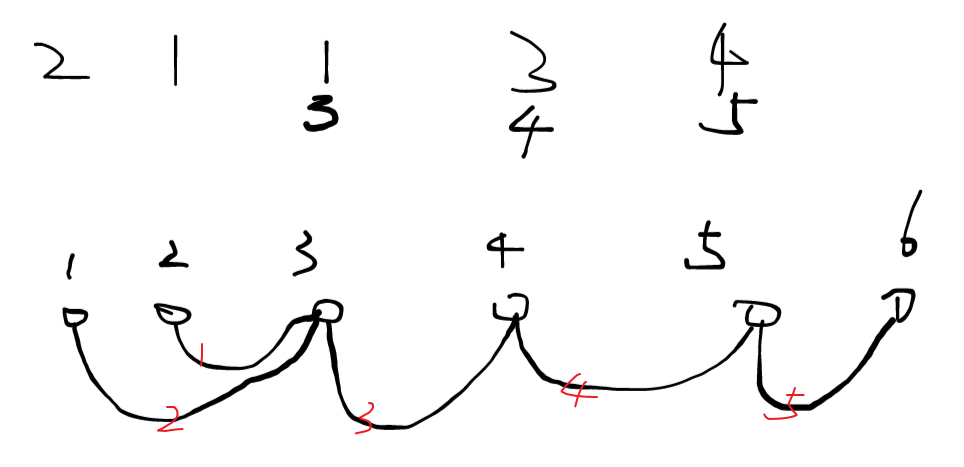
• 过程模拟图：

• 主要思路：路径压缩，前面使用暴力算法，每次遍历一个新数时，都要遍历一遍该数前所有的数，时间复杂度为$O(n^2)$，而使用路径压缩（也就是并查集）时间复杂度缩减至$o(n)$。路径压缩就是将当前节点存储父节点（父节点要比当前节点的值大1），这样每次遍历我们都可以直接添加到之前没有出现的数，不需要再去循环遍历+1后这个数是否已经存在了。

  比如：每次我们遍历一个数时，都提前将这个数的父节点标记为当前数的+1，也就是当遍历2时，它的父节点我们就设置为3；之后我们遍历1时，将1的父节点设置为2的父节点，同样是3；之后再遍历1时，发现重复，就可以直接将值设置为3，不需要+1设置为2，再循环遍历判断是否已存在，然后再进行+1最终设置为3，这样就减少了一次循环，直接将时间复杂度由$O(n^2)$变为了$O(n)$

题解

• 解法一：暴力（测试过4个，6个超时）

  import java.util.Scanner;public class Main {static int[] arr;public static void main(String[] args) {Scanner sc = new Scanner(System.in);int n = sc.nextInt();arr = new int[n+1];for (int i = 1; i < arr.length; i++) {arr[i] = sc.nextInt();}for (int i = 1; i < arr.length; i++) {find(i);}for (int i = 1; i < arr.length; i++) {System.out.print(arr[i]+" ");}}private static void find(int i) {boolean f = false;for (int j = 0; j < i; j++) {if(arr[j] == arr[i]) {f = true;break;}}if(f) {// 存在重复元素arr[i]++;find(i);}}
  }
  

• 解法二：并查集（过8个，超时2个）

  import java.util.Scanner;public class Main{static int[] f = new int[2000000]; // 存放1~n个节点（长度要大于最大元素）public static void main(String[] args) {// 输入Scanner sc = new Scanner(System.in);int n = sc.nextInt();int[] arr = new int[n];// 初始化ffor (int i = 0; i < f.length; i++) {f[i] = i;}for (int i = 0; i < arr.length; i++) {arr[i] = sc.nextInt();}for (int i = 0; i < arr.length; i++) {// 将当前元素的根节点赋值给当前元素arr[i] = find(arr[i]);// 将当前元素的根节点往后移动一位f[arr[i]] = find(arr[i]+1);}// 输出for (int i = 0; i < arr.length; i++) {System.out.print(arr[i]+" ");}}/*** 获取x的根节点* @param x* @return*/static int find(int x) {if(f[x] == x) {// 当前节点是根节点return x;}f[x] = find(f[x]);return f[x];}
  }
  

  优化：将找寻根节点的操作放到输入的循环语句中，减少一个for循环，但仍然有一个超时！

  import java.util.Scanner;public class Main{static int[] f = new int[2000000]; // 存放1~n个节点public static void main(String[] args) {// 输入Scanner sc = new Scanner(System.in);int n = sc.nextInt();int[] arr = new int[n];// 初始化ffor (int i = 1; i < f.length; i++) {f[i] = i;}// 优化的部分for (int i = 0; i < arr.length; i++) {arr[i] = sc.nextInt();// 将当前元素的根节点赋值给当前元素arr[i] = find(arr[i]);// 将当前元素的根节点往后移动一位f[arr[i]] = find(arr[i]+1);}// 输出for (int i = 0; i < arr.length; i++) {System.out.print(arr[i]+" ");}}/*** 获取x的根节点* @param x* @return*/static int find(int x) {if(f[x] == x) {// 当前节点是根节点return x;}return find(f[x]);}
  }
  

  再次优化：寻找父节点的同时进行路径压缩

  // 第一段（优化）static int find(int x) {if(f[x] == x) {// 当前节点是根节点return x;}f[x] = find(f[x]);return find(f[x]);}
  // 第二段static int find(int x) {if(f[x] == x) {// 当前节点是根节点return x;}return find(f[x]);}
  

  两段代码的主要区别在于第二段代码中没有更新并查集的父节点，每次都通过递归查找到最终的祖先节点，而第一段代码中则在递归回溯的过程中顺便更新了每个节点的父节点，从而使得整个并查集形成了一个树形结构。

  由于第二段代码没有更新父节点，所以在进行大量查找操作时，每次都需要递归查找到最终的祖先节点，而这个过程是比较耗时的。而第一段代码中通过更新父节点的方式，可以使得后续查找操作更加快捷。

  因此，当数据量较大时，第一段代码的效率要明显高于第二段代码，第二段代码容易出现超时的情况。

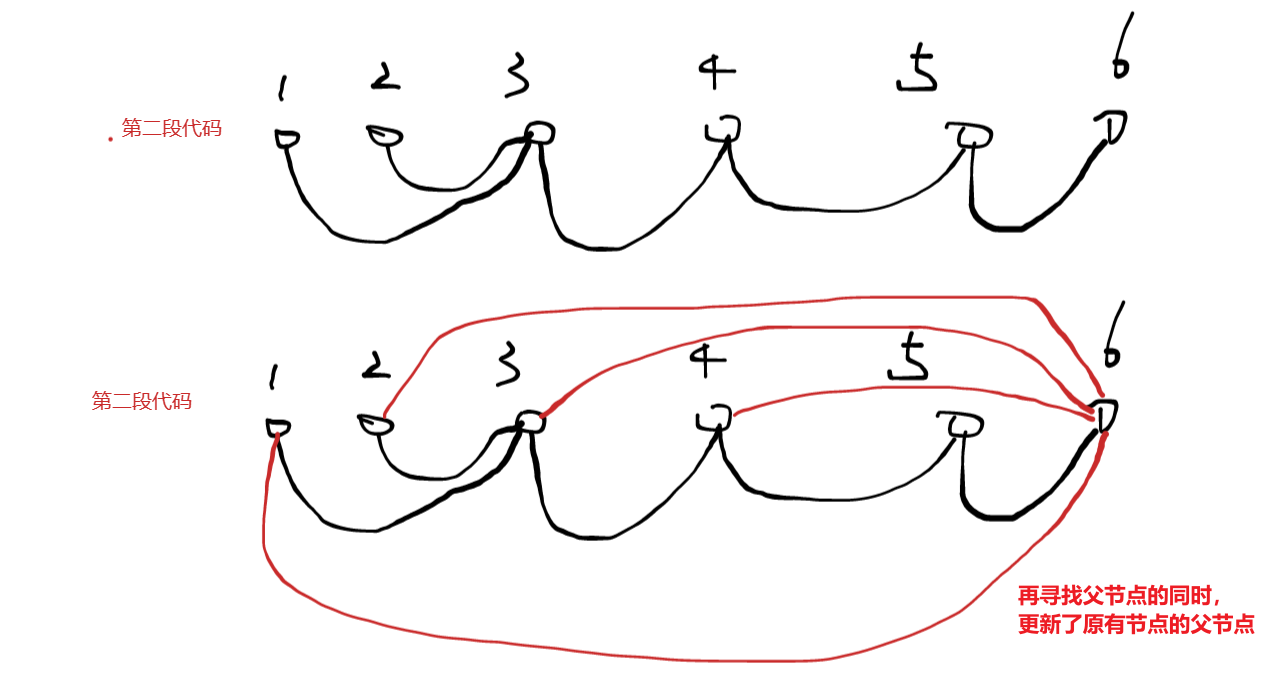
  两者的区别如下图所示：

  第一段代码，再寻找父节点的同时，更新了之前节点的父节点，从而进一步压缩路径了。

  1，2是父节点是3，而3的父节点是4，4的父节点是5，5的父节点是6，有一定的冗余，第一段代码会在寻找父节点的同时，将之前的已经有父节点的节点，重新更新当前罪行的父节点，也就1，2，3，4直接父节点变为了6，这就大大提高了后续寻找1，2，3，4它们父节点的效率，从而降低时间复杂度

  
  经过不断优化，最终全过了😄
  最终的代码：

import java.util.Scanner;public class Main{static int[] f = new int[2000000];public static void main(String[] args) {Scanner sc = new Scanner(System.in);int n = sc.nextInt();int[] arr = new int[n];for (int i = 1; i < f.length; i++) {f[i] = i;}for (int i = 0; i < arr.length; i++) {arr[i] = sc.nextInt();arr[i] = find(arr[i]);f[arr[i]] = find(arr[i]+1);}for (int i = 0; i < arr.length; i++) {System.out.print(arr[i]+" ");}}static int find(int x) {if(f[x] == x) {return x;}f[x] = find(f[x]);return f[x];}
}