网站建设的基本规范有什么/网站建设公司苏州

训练用例

（xi，yi），此元祖成为训练用例数据集

训练数据集

（xi，yi），i=1,2,……m，此m个训练用例成为训练数据集，工资和年龄，两个特征，拟合

输入数据集

用X来表示输入数据集

输出数据集

用y来表述输出数据集，最终可以银行可以借到多少钱

机器学习目标

机器学习的目标是，给定一个训练数据集，训练一个函数h：x->y，使得h(x)是一个好的预测函数，“好”的意思是给一个xi，通过h(x)计算出来的y，非常接近实际的yi，即y与yi的偏差最小，即拟合度最高。

线性回归

回归：区间中某一个值
分类：类别值
线性回归是很常见的一种回归，线性回归可以用来预测或者分类，主要解决线性问题。
1）线性回归中的“线性”描述的对象是谁？

线性指的是假设函数（如h(x)=θ0 + θ1x）中自变量x（即输入数据集）的系数θ的性质，即θ是线性的。

2）线性回归中的“回归”描述的对象是谁？

指假设函数h(x)和实际的数据集拟合度最高

3）多元线性回归中的“多元”描述的对象是谁？

多元表示训练数据集中每组用例有多个特征变量，

比如含有n元表示训练用例中有n个特征变量，

如第一组n元训练用例可表示为：（x11，x12，x13，……，x1n，y1），xij表示第i组用例中的第j个特征变量

假设函数

hypothesis function，记做h(x)

机器学习中被训练的函数就是假设函数。

简单线性回归的假设函数和多元线性回归的假设函数不同，可详见下面内容。

代价函数

cost function，记做J(θ)。

用来度量假设函数的拟合度、精确度。

J(θ)函数值越小表示h(x)预测出来的数据集与实际数据集的偏差越小。

所以J(θ)函数值最小时的元祖(θ0，θ1，……，θm)，此元祖对应的h(x)是拟合度最高的假设函数。矩阵运算

简单线性回归

简单线性回归只有一个自变量x。

简单线性回归的假设函数
h(x)=θ0+θ1x
权重参数，偏置参数
这个函数图形是一条直线，称为回归线，h(x)是在一个给定特征值x下的y的期望值

简单线性回归的代价函数

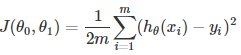
很明显，此代价函数主要计算任务就是计算y的方差的均值。

这个均值越小，说明拟合度越高。而计算的过程，变成了求代价函数最小值的过程。从而转变成了高等数学问题中求函数最小值时对应的坐标的问题，就是这么个思路。

简单线性回归的梯度下降算法的推导公式

θ公式的推导过程详见：简单线性回归的梯度下降中θ的推导过程

误差

误差，独立同分布，服从均值为0，方差为高斯分布


似然函数，参数估计，根据数据服从怎么样的规则，数据推参数。极大似然估计，称为真实值得概率越大越好

评估方法

多元线性回归

多元指的是每个训练用例中有多个特征变量x

使用xi表示训练集中的第i组训练用例

使用xij表示第i组用例中的第j个特征变量x

使用n表示每组用例的特征数，所以每组用例的元祖是(x1, x2, ……，xn)。

使用m表示训练用例的总数，即训练数据集有m组训练用例

数据训练集的整体如下所示：

(X11，X12，X13，……，X1n，y1)

(X21，X22，X23，……，X2n，y2)

            ……

(Xi1，Xi2，Xi3，……，Xin，yi)

            ……

(Xm1，Xm2，Xm3，……，Xmn，yn)

多元线性回归的假设函数

h(Xi) = θ0 + θ1Xi1+θ2Xi2+……+θnXin，其中i=1,……,m，表示训练数据集有m个训练用例，每个训练用例有n个特征变量x。

多元线性回归的假设函数的矩阵乘法表示方式

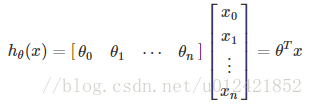
多元线性回归的梯度下降算法的推导公式
每个θ的推导过程，和简单线性回归的梯度下降中的θ的推导过程一模一样

详见：简单线性回归的梯度下降中θ的推导过程。

感想与收获

边应用一边学习，看到不懂得知识点，就研究透彻一下。看一下博客

这样，按照线性代数的理论，对于lambda不为0，逆矩阵是一定存在的。下面看看代码：

def linear_regression(x_arr, y_arr, lam=0.2):x_mat = np.mat(x_arr).Ty_mat = np.mat(y_arr).Tx_tx = x_mat.T * x_matdenom = x_tx + np.eye(np.shape(x_mat)[1]) * lam# if lam == 0.0if np.linalg.det(denom) == 0.0:print('This matrix is singular, cannot do inverse')returnws = denom.I * (x_mat.T * y_mat)return ws

再看一下调用的demo：

if __name__ == '__main__':x_vals = np.linspace(0, 1, 1000)y_vals = x_vals + np.random.normal(0, 1, 1000)ws = linear_regression(x_vals, y_vals)predict = 20 * wsprint(predict.A[0][0])

我们构造了x和y使其尽可能满足x=y，不过在其中加入了标准正态分布的噪声，求出ws之后，我们预测了x=20的y值。下面是我运行一次的结果，预测效果还不错：

19.690649736617942

另一种思路是我们直接使用梯度下降法求取平方误差的最小值，这里我们使用tensorflow实现。首先导入需要的包并准备数据：

import numpy as np
import tensorflow as tflearning_rate = 0.05
batch_size = 50x_vals = np.linspace(0, 1, 1000)
y_vals = x_vals + np.random.normal(0, 1, 1000)
x_vals.resize((x_vals.shape[0], 1))
y_vals.resize((y_vals.shape[0], 1))

然后构造模型，x_data和y_target是占位符，在训练模型时传入，w是我们训练模型希望得到的目标变量：

sess = tf.Session()
x_data = tf.placeholder(shape=[None, 1], dtype=tf.float32)
y_target = tf.placeholder(shape=[None, 1], dtype=tf.float32)
w = tf.Variable(tf.random_normal([1, 1]))
model_output = tf.matmul(x_data, w)

定义均方误差，然后使用梯度下降法进行优化，求取最小值

loss = tf.reduce_mean(tf.square(y_target - model_output))
init = tf.global_variables_initializer()
sess.run(init)
my_opt = tf.train.GradientDescentOptimizer(learning_rate)
train_step = my_opt.minimize(loss)

最后，使用随机梯度下降法进行训练，并输出测试结果

for i in range(500):rand_index = np.random.choice(len(x_vals), size=batch_size)rand_x = x_vals[rand_index]rand_y = y_vals[rand_index]sess.run(train_step, feed_dict={x_data: rand_x, y_target: rand_y})[k] = sess.run(w)
predict = 20 * k
print(predict[0])
一次运行结果：

19.260855
至此，我们使用两种方式实现了线性回归，第一种方式比较直接，直接实现算法，第二种方法借助于tensorflow通过梯度下降算法求取了最优值。

KaTeX数学公式

您可以使用渲染LaTeX数学表达式 KaTeX:

Gamma公式展示 $\Gamma (n)=(n-1)!\forall n\in \mathbb{N}$ 是通过欧拉积分

$$\Gamma (z)={\int }_0^{\infty }{t}^{z-1}{e}^{-t}dt.$$

你可以找到更多关于的信息 LaTeX 数学表达式[here][1].

新的甘特图功能，丰富你的文章

• 关于 甘特图 语法，参考 [这儿][2],