怎么修改收录网站的标题/网站单向外链推广工具
王凯强:“全息”:一个大家耳熟却不能详的词汇zhuanlan.zhihu.com
![]()
![]() 是虚数单位,
是虚数单位,![]() 表示空间位置,
表示空间位置, ![]() 表示振幅,
表示振幅, ![]() 表示相位。
表示相位。![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() :
: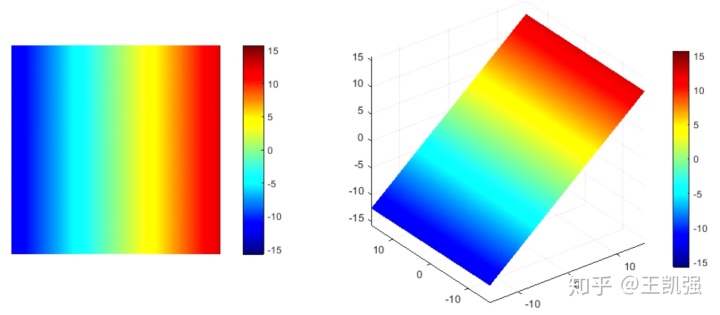
图1 物光相位, 左:二维, 右:三维 ![]() 是一个左边低右边高的斜面。
是一个左边低右边高的斜面。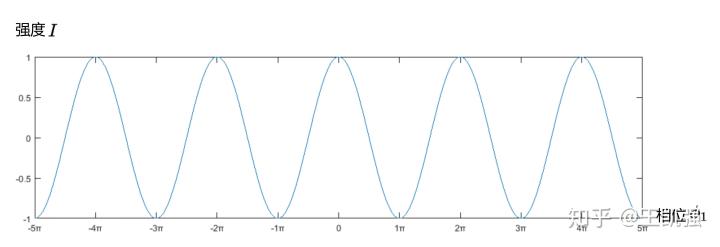
图2 余弦函数,横轴为相位值,纵轴是强度值 ![]() 是π的偶数倍时,强度
是π的偶数倍时,强度 ![]() 取最大值;(是不是和“干涉相长”的条件一样?)
取最大值;(是不是和“干涉相长”的条件一样?)![]() 是π的奇数倍时,强度
是π的奇数倍时,强度 ![]() 取最小值;(是不是和“干涉相消”的条件一样?)
取最小值;(是不是和“干涉相消”的条件一样?)![]() 的取值范围是[-1, 1]。
的取值范围是[-1, 1]。![]() 取余弦,得到强度
取余弦,得到强度 ![]() ,并以动态形式从左往右依次呈现出来:
,并以动态形式从左往右依次呈现出来:
图3 cos(左图相位)=右图强度 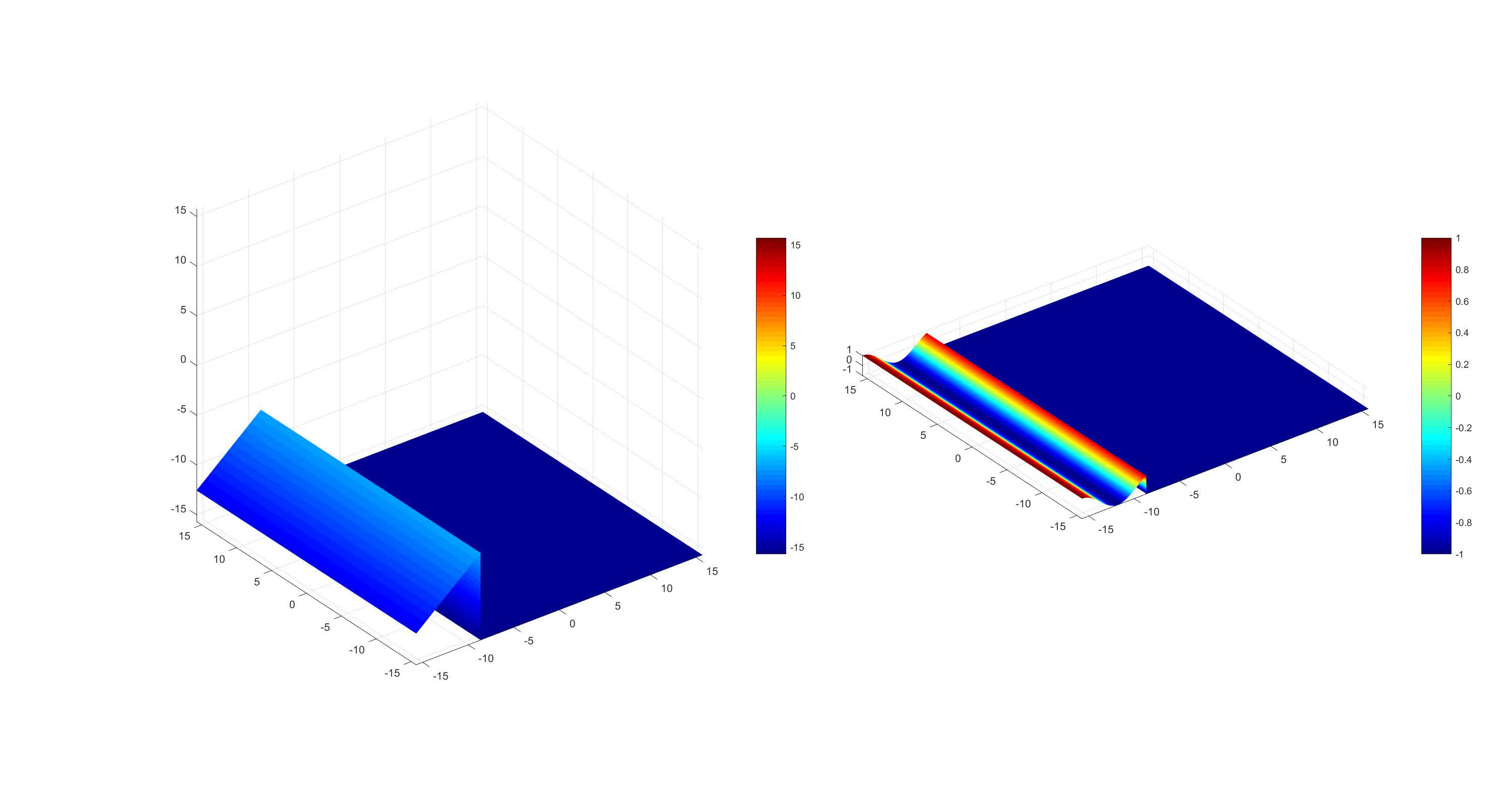 cos(左图相位)=右图强度https://www.zhihu.com/video/1175775135746887680
cos(左图相位)=右图强度https://www.zhihu.com/video/1175775135746887680

↑↑↑↑介绍了什么是“全息”↑↑↑↑
我们知道了“哪里高哪里低”的相位信息通过干涉被记录在条纹状的强度信息中。
这篇的目的,主要是帮助大家理解,“相位信息是如何被记录在条纹中的”。
(字数700+,配图3,公式较多,建议阅读时长15-25分钟,转载请私聊。)
1 光波场的复振幅表示
我们知道光波场的复振幅表达式是这样的:
其中
为了看起来方便,后面的公式中我们省略,就像这样:
2 两束光干涉的光强表达式
预备知识:1. 复数的共轭为2. 欧拉公式3. 余弦函数为偶函数,即4. 正弦函数为奇函数,即
5. 加法和乘法是线性映射,不会影响分布规律
物光的复振幅表达式:
参考光的复振幅表达式:
那么物光和参考光共轭的表达式:
两束光干涉后的光强表达式(一步一步推导):
令为相位差
,
为了把注意力集中到相位信息上,我们假设两束光的振幅和都为常数
我们用没有倾角的平面光作为参考光,即,相位
加法和乘法是线性映射,不会影响分布规律,所以我们把加法和乘法去掉
至此,我们得到了精简后的物参光干涉光强表达式:
3. 利用实例进行形象化的理解(蓝色数值最小,红色数值最大)
物光相位

我们可以看到,物光相位
接下来,先看一下余弦函数的图像:

有什么规律?
当相位
当相位
强度
现在,我们对相位


看完动图和视频,想必大家应该心里有数了吧?
一句话总结:
相位信息通过取余弦的方式被记录在条纹状的干涉强度中。
