西宁做网站公司排名/百度搜索推广是什么
首先,我们来看下面的例子。
【例1】通过给定的身高、体重组合与对应性别的数据,实现对未知身高、体重组合的性别预测。
在这个例子中,输入空间为所有可能的身高、体重组合(二维特征向量),记作 X⊆R2\mathcal{X} \subseteq R^2X⊆R2 ;输出空间为所有可能的性别(只有两个取值的离散变量),记作Y⊆{+1,−1}\mathcal{Y} \subseteq \{+1,-1\}Y⊆{+1,−1}。
输入实例xxx的特征向量记作x=(x(1),x(2))T∈Xx = (x^{(1)},x^{(2)})^T \in \mathcal{X}x=(x(1),x(2))T∈X,x(1)x^{(1)}x(1)和x(2)x^{(2)}x(2)分别表示实例的第一个特征(身高)和第二个特征(体重)。
因为输入变量为连续变量,输出变量为只有两个取值的离散变量,所以这是一个二类分类问题。
我们希望得到一个由输入空间到输出空间的函数f(x)f(x)f(x)(决策函数),可以将输入的实例xxx划分到两类中。
身高作为X轴,体重作为Y轴,不同性别用不同颜色表示,将输入的实例绘制到平面直角坐标系中(如下图)。
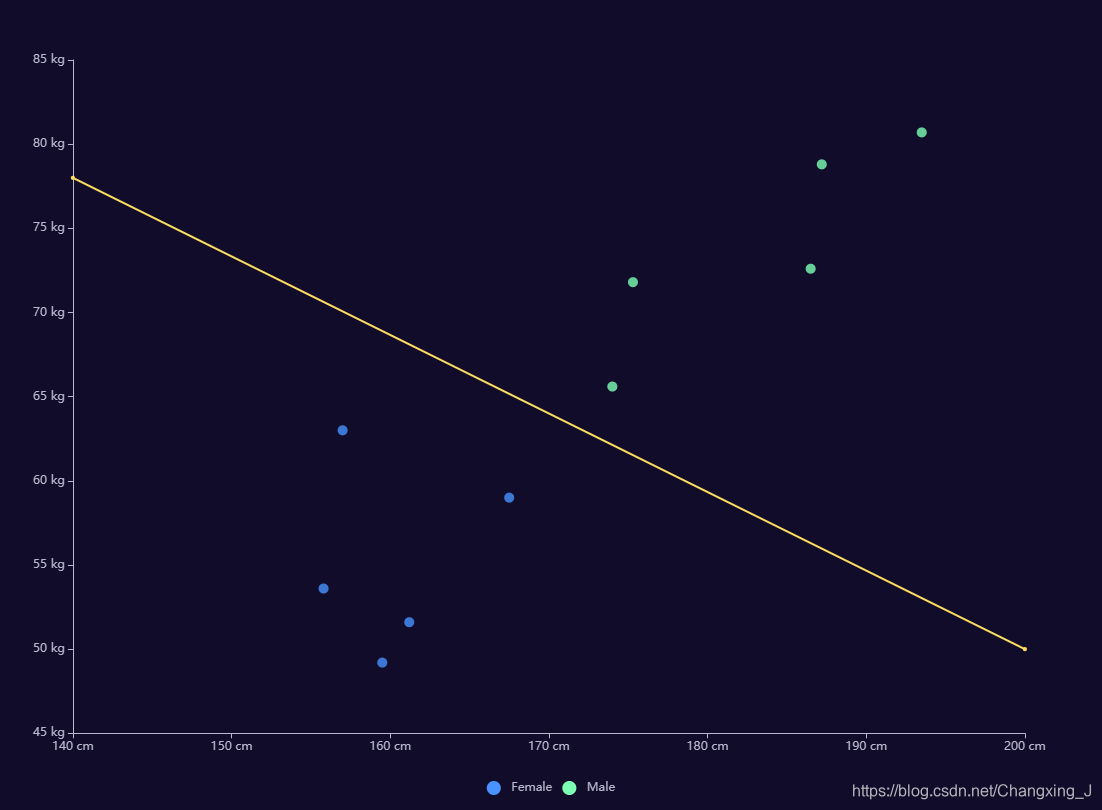
上图ECharts源码 : ECharts示例图001:二维感知机示例图(2维/散点+折线图)
可以看到,女性(蓝色)样本点主要集中于左下区域,男性(绿色)样本点主要集中于右上区域。
于是很自然地想到:或许可以通过构造一条直线(例如上图中的黄线),将平面划分为左下、右上两个区域。将所有位于左下区域的未知样本点估计为女性,将所有位于右上区域的样本点估计为男性。当存在某条直线可以将女性样本点和男性样本点正确地划分到直线两侧时,则必然有无穷多条满足要求的直线。
根据直线的一般式w1x(1)+w2x(2)+b=0w_1 x^{(1)} + w_2 x^{(2)} + b =0w1x(1)+w2x(2)+b=0,这个思路可以表示为由输入空间到输出空间的函数:
f(x)={+1,w1x(1)+w2x(2)+b≥0−1,w1x(1)+w2x(2)+b<0f(x) = \begin{cases} +1, & w_1 x^{(1)} + w_2 x^{(2)} + b \ge 0\\ -1, & w_1 x^{(1)} + w_2 x^{(2)} + b < 0\\ \end{cases} f(x)={+1,−1,w1x(1)+w2x(2)+b≥0w1x(1)+w2x(2)+b<0
当特征向量为二维时, 感知机对应于输入空间(二维欧式空间)中将实例划分为正负两类的分离直线,函数f(x)f(x)f(x)即为感知机的定义式。
将输入的特征向量一般化到n维,则感知机对应于将输入空间(n维欧式空间)划分为正负两类的分离超平面。
用向量表示特征向量和参数,输入实例xxx的特征向量记作x=(x(1),x(2),⋯,x(n))T∈X⊆Rnx=(x^{(1)},x^{(2)},\cdots,x^{(n)})^T \in \mathcal{X} \subseteq R^nx=(x(1),x(2),⋯,x(n))T∈X⊆Rn,参数记作w=(w1,w2,⋯,wn)T∈Rnw=(w_1,w_2,\cdots,w_n)^T \in R^nw=(w1,w2,⋯,wn)T∈Rn,此时分离超平面可以表示为w⋅x+b=0w·x+b=0w⋅x+b=0,感知机可以表示为由输入空间到输出空间的函数:
f(x)={+1,w⋅x+b≥0−1,w⋅x+b<0f(x) = \begin{cases} +1, & w·x + b \ge 0\\ -1, & w·x + b < 0\\ \end{cases} f(x)={+1,−1,w⋅x+b≥0w⋅x+b<0
此时,www为分离超平面的法向量,bbb为分离超平面的截距。
下面给出n维特征向量时感知机的标准定义。
【定义1】感知机 (来自李航的《统计学习方法》P. 35)
假设输入空间(特征空间)是 X⊆Rn\mathcal{X} \subseteq R^nX⊆Rn ,输出空间是 Y⊆{+1,−1}\mathcal{Y} \subseteq \{+1,-1\}Y⊆{+1,−1} 。输入 x⊆Xx \subseteq \mathcal{X}x⊆X 表示实例的特征向量,对应于输入空间(特征空间)的点;输出y∈Yy \in\mathcal{Y}y∈Y表示实例的类别。由输入空间到输出空间的如下函数:
f(x)=sign(w⋅x+b)f(x)=sign(w·x+b) f(x)=sign(w⋅x+b)
称为感知机。其中, www 和 bbb 为感知机模型参数, w∈Rnw \in R^nw∈Rn 叫作权值或权值向量, b∈Rb \in Rb∈R 叫作偏置, w⋅xw·xw⋅x 表示 www 和 xxx 的内积。 signsignsign 是符号函数,即
sign(x)={+1,x≥0−1,x<0sign(x)=\begin{cases} +1, & x \ge 0\\ -1, & x < 0\\ \end{cases} sign(x)={+1,−1,x≥0x<0
感知机模型对数据的要求:训练数据集中需存在某个超平面能够将数据集的正实例点和负实例点完全正确地划分到超平面的两侧,即训练数据集是线性可分的。因为只有当训练数据集是线性可分时,感知机学习算法才是收敛的;如果训练数据集线性不可分,则感知机学习算法不收敛,迭代结果会发生震荡。当训练数据集线性不可分时,可以使用线性支持向量机。
感知机模型的学习过程:依据训练数据集求得感知机模型,即求得模型参数www和bbb。
感知机模型的预测过程:通过学习得到的感知机模型,计算新的输入实例所对应的输出类别。
感知机模型的类别划分:
- 用于解决二类分类问题的监督学习模型
- 非概率模型:模型取函数形式(而非概率模型的条件概率分布形式)
- 线性模型:模型函数为线性函数
- 参数化模型:模型参数的维度固定
- 判别模型:直接学习决策函数f(x)f(x)f(x)
感知机模型的主要优点:算法简单,易于实现。
感知机模型的主要缺点:要求训练数据集线性可分。
