一、前言

最近在准备笔试题时，经常看到求解某序列前K个最大数/最小数/最常出现元素的题目。最后发现这些题目的解法都十分相似，便阅读了一些资料，写下这篇文章，希望对大家有用。

二、算法模式

其实，对于 [ 任何要求我们找到一个给定集合中最前面的/最小的/最常出现的K个元素的问题 ] 都可以总结为一类问题——“Top K 问题”。

对于这类问题，如果数据量不是很大，快速排序倒是可以解决。但是当数据量过于庞大的话，这样的解决方案便不再提倡，这里给出一种通用解决方案——“Top k 算法模式”。

什么是“Top k算法模式”呢？

Top k 算法模式就利用Heap（堆）来跟踪给定集合的前K个元素，从而一次性的处理一个给定元素集中前K个元素的问题。

2.1、工作模式

1、根据给定元素集合，将k个元素插入到min_heap或者max_heap中
2、利用heap的性质进行迭代的处理剩余的元素。例如你需要找到一个给定元素集合中的前k个大的元素，则可以先将前k元素建立min_heap，然后遍历后续的元素，当pop_heap元素小于当前遍历的元素T[index]，则将堆顶元素换成当前遍历的元素T[index]，再维持min_heap。最后便可以得到一个前k大的元素。如下图：
步骤一：对集合区间[begin,k)元素建立max_heap（大顶堆）

步骤二：遍历区间[k,last)元素，比较堆顶元素与当前遍历元素，如果遍历值大于当前堆顶元素，则互换堆顶元素与当前遍历元素，同时维护交换元素后的堆数据结构为大顶堆。




步骤三：最后对集合区间[begin,k)进行一次堆排序，便可获得前k个元素的有序数列集合，从而降低了对大量数据的排序使用。

那么我们何时使用该算法模式可以获得较好的性能呢？

这里给出一些拙见，希望对大家有用：
1、寻找给定集合中最大的/最小的/最常出现的k个元素
2、对给定集合进行排序从而找到一个确定元素，如寻找第k个元素

Leetcode 相关问题：

三、实例分析

题目：[ 假设有一个容器，存放了100万个数值，但是我们只对其中最小的100个元素的顺序感兴趣。要求获得前100个元素的从小到大的有序顺序。]

题目分析：拿到这道题，其实我们可以对容器的全部内容进行排序，然后选择前100个元素即可，但这样处理会使得效率低下，这时我们就可以使用我们提到的[ Top k算法模式 ]。具体的代码实现，这里就不仔细描述。

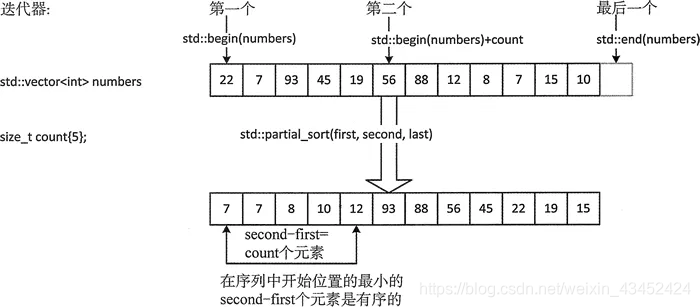
其实在C++的STL（Standard Template Library）中便实现了这种算法模式，在方法 [ partial_sort：对集合中部分元素进行排序，从而获得前k个元素的有序序列 ] 就得到了很好的体现。 这里一起来看看STL中的源码是如何描述的？

四、“partial_sort”——STL源码分析

4.1、partial_sort 原理

1、首先，对给定集合内区间为[ first , middle ）元素构造大顶堆（make_heap）。
2、其次，遍历剩余区间[ middle , last）中的元素，剩余区间的每个元素均与大顶堆的堆顶元素进行比较，若堆顶元素较小，则交换堆顶元素与遍历得到的元素值( pop_heap)，并重新调整该大顶堆以维持该堆为大顶堆 （adjust_heap）。
3、遍历结束后，[ first,middle ）区间内的元素便是排名在前的k个元素，之后再对该堆做一次堆排序( sort_heap )即可得到最后的前k个有序元素的结果。

4.2、partial_sort()算法执行步骤详解

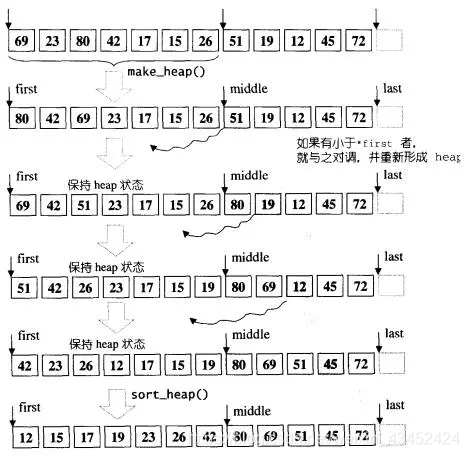
源码五分钟，实践五小时，一起看看！！！！

4.3、Partial_sort方法调用关系图：

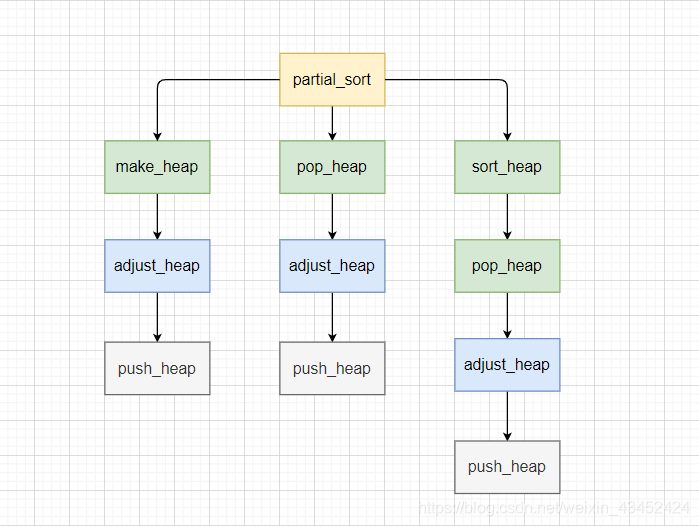
4.4、C++源码分析

首先，我们先来看看partial_sort()的源码。

void __partial_sort(RandomAccessIterator first, RandomAccessIterator middle,RandomAccessIterator last, T*) {make_heap(first, middle);  //将区间[first, middle)构造为一个堆结构for (RandomAccessIterator i = middle; i < last; ++i)if (*i < *first)     //遍历堆以外的元素，并将更符合要求的元素放入堆中__pop_heap(first, middle, i, T(*i), distance_type(first)); // first值放i中，i的原值融入heap并调整sort_heap(first, middle); // 对最终的堆进行排序
}

make_heap函数方法（算法）：将一段指定的数据排列为max_heap

void __make_heap(RandomAccessIterator first, RandomAccessIterator last, T*,Distance*) {if (last - first < 2) return; // 如果长度为 0 或 1，不必重新排列  Distance len = last - first;// 找出第一个需要重新排列的子树头部（即最后一个子树），以parent标记。由于任何叶子节点都不需要处理。// holeIndex ：标注为需要调整的元素Distance parent = (len - 2)/2; while (true) {// 重排以parent为首的子树，以len为操作范围__adjust_heap(first, parent, len, T(*(first + parent)));if (parent == 0) return; // 走完根节点，结束parent--; // 向前排列前一个节点}
}

__adjust_heap函数方法（算法）：从first开始调整len个元素，holeIndex(洞号)为需要调整的值，其值用value（洞值）存放，最终获得一个max_heap。

void __adjust_heap(RandomAccessIterator first, Distance holeIndex,Distance len, T value) {Distance topIndex = holeIndex;Distance secondChild = 2 * holeIndex + 2; // holeIndex的右子节点while (secondChild < len) {// 比较holeIndex两个子节点的值，用secondChild代表值较大的子节点if (*(first + secondChild) < *(first + (secondChild - 1)))secondChild--;   // 令较大子值为洞值，注意：原已在函数形参value中得以保存*(first + holeIndex) = *(first + secondChild); // 再让洞号下移到左子节点处，holeIndex = secondChild;// 算出新的洞节点的右子节点secondChild = 2 * (secondChild + 1);}// 如果没有右子节点，只有左子节点if (secondChild == len) { // 令左子节点为洞值，然后将洞号下移到左子节点*(first + holeIndex) = *(first + (secondChild - 1));holeIndex = secondChild - 1;}// 将原洞值push到新的洞号中。// 以下语句的效果类似于：*(first + holeIndex) = value; __push_heap(first, holeIndex, topIndex, value);
}

__push_heap函数方法（算法）：实现将新元素value push到max_heap中 [ topIndex,holeIndex ]的合适位置中，其中max_heap的起始位置为first。

void __push_heap(RandomAccessIterator first, Distance holeIndex,Distance topIndex, T value) {Distance parent = (holeIndex - 1) / 2;  // 找到父节点// 当尚未达到顶端， 且父节点的值小于新值（不符合max-heap的次序特性）while (holeIndex > topIndex && *(first + parent) < value) {*(first + holeIndex) = *(first + parent); // 移动父值到洞号处holeIndex = parent; // 调整洞号为父节点parent = (holeIndex - 1) / 2; // 新洞的父节点}  // 循环到顶端，或者满足max-heap的顺序为止*(first + holeIndex) = value; // 将新值放入循环完得到的洞号，完成push操作
}

__pop_heap函数方法（算法）：互相交换在heap中所指的元素

inline void __pop_heap(RandomAccessIterator first, RandomAccessIterator last,RandomAccessIterator result, T value, Distance*) {*result = *first; // 将heap顶端元素值放入 result中// 重新调整heap，洞号为0，欲调整的新值为value__adjust_heap(first, Distance(0), Distance(last - first), value);
}

可以观察到，其实 __pop_heap 函数完成了 partial_sort 函数中，当 *i < *first 时，代码中互相交换i所指元素和 first 所指元素。通过将 first 元素放入指定的 result，然后再用新值 value去 调整 max_heap。

sort_heap函数方法（算法）：将[ first , middle)中的元素由堆序变为增序排序。每次弹出堆的最大值并放入尾部，然后缩小堆的范围，循环执行弹出操作直到堆只剩下最后一个元素。

void sort_heap(RandomAccessIterator first, RandomAccessIterator last) {while (last - first > 1)  // 直到只剩一个元素为止pop_heap(first, last--); // 每执行一次，范围缩小一格
}inline void pop_heap(RandomAccessIterator first, RandomAccessIterator last) {__pop_heap_aux(first, last, value_type(first));
}inline void __pop_heap_aux(RandomAccessIterator first,RandomAccessIterator last, T*) {// 将first元素值（即最大值）放入last-1，然后重调[first, last-1)为max-heap__pop_heap(first, last-1, last-1, T(*(last-1)), distance_type(first));
}

4.5、Java模拟实现 partial_sort()

partial_sort函数：

// partial_sort 函数public boolean partial_sort(T[] t,int nSize) {int total = t.length;make_heap(t,nSize); //建立大顶堆for(int i=nSize;i<total;i++) {if(cmp.less(t[i], t[0])) {pop_heap(t,nSize,i);}}sort_heap(t,nSize);return true;}

make_heap函数：

// make_heap函数public boolean make_heap(T[] t,int nSize) {if(nSize>=2) { //确保至少有两个元素for(int i=nSize/2;i>0;) {--i;adjust_heap(t,i,nSize);}}return true;}

adjust_heap函数：

// adjust_heap 函数public boolean adjust_heap(T[] t,int pos,int nSize) {int j=pos;T v = t[pos];int k = 2*pos+2;for(;k<nSize;k=2*k+2) {if(cmp.less(t[k], t[k-1])) {--k;}t[pos] = t[k];pos = k;}if(k==pos) {t[pos] = t[k-1];pos = k-1;}push_heap(t,pos,j,v);return true;}

sort_heap函数:

  //sort_heap 函数public boolean sort_heap(T[] t, int l) {for(;l>1;--l) {pop_heap(t,l-1,l-1);}return true;}

pop_heap函数：

//pop_heap 函数public boolean pop_heap(T[] t,int m,int i) {swap(t,0,i); //交换两集合元素adjust_heap(t,0,m);return true;}

push_heap函数：

//push_heap 函数Java实现public boolean push_heap(T[] t , int h , int j ,T v) {for(int i=(h-1)/2;j<h&&cmp.less(t[i], v);i=(h-1)/2) {t[h] = t[i];h = i;}t[h] = v;return true;}

Comparator比较器： 定义泛型比较器

public class Comparator extends AbstractIComparator<Integer>{public boolean equal(Integer x, Integer y) {if(x == y)return true;return false;}public boolean less(Integer x, Integer y) {if(x < y)return true;return false;}
}

测试：

public class Test {public static void main(String[] args) {IComparator<Integer> cmp = new Comparator();Algorithm<Integer> obj = new Algorithm<Integer>(cmp);Integer[] t = {12,9,0,11,29,3,91,20,5,44};obj.partial_sort(t, 5);System.out.print("排序后顺序为：");for(int i=0;i<10;i++) {System.out.print(t[i]+" ");}}
}

测试结果：

参考文章

[1] STL之partial_sort算法源码讲解:https://blog.csdn.net/ggq89/article/details/88817085
[2] 《Java设计模式深入研究》