【参考资料】

从B树、B+树、B*树谈到R 树

【B树解释】

B树是一棵树，不同的是该树的最多有m个子节点，至少floor（m/2）个子节点（根节点除外，根节点最少可以有两个子节点。），但是里面包含关键字数量比当前的子节点少1，在没有子节点的情况下，关键字数量在 floor（m/2）-1到m-1之间。

左边子节点的关键字都比父亲节点对应的关键字小，右边子节点的关键字都比对应父亲节点的关键字大。

这样描述大家可能会迷迷糊糊，现在摘录 july的部分图文进行解释：

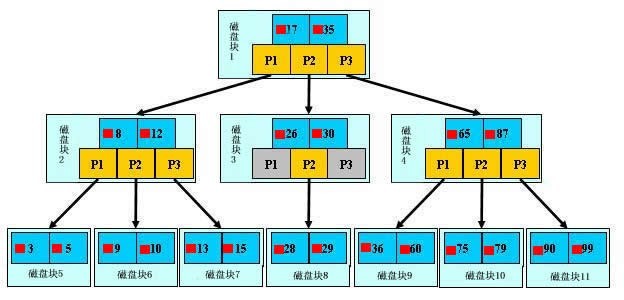
    B 树又叫平衡多路查找树。一棵m阶的B 树 (注：切勿简单的认为一棵m阶的B树是m叉树，虽然存在四叉树，八叉树，KD树，及vp/R树/R*树/R+树/X树/M树/线段树/希尔伯特R树/优先R树等空间划分树，但与B树完全不等同)的特性如下：

1. 树中每个结点最多含有m个孩子（m>=2）；
2. 除根结点和叶子结点外，其它每个结点至少有[ceil(m / 2)]个孩子（其中ceil(x)是一个取上限的函数）；
3. 若根结点不是叶子结点，则至少有2个孩子（特殊情况：没有孩子的根结点，即根结点为叶子结点，整棵树只有一个根节点）；
4. 所有叶子结点都出现在同一层，叶子结点不包含任何关键字信息(可以看做是外部接点或查询失败的接点，实际上这些结点不存在，指向这些结点的指针都为null)；（读者反馈@冷岳：这里有错，叶子节点只是没有孩子和指向孩子的指针，这些节点也存在，也有元素。@研究者July：其实，关键是把什么当做叶子结点，因为如红黑树中，每一个NULL指针即当做叶子结点，只是没画出来而已）。
5. 每个非终端结点中包含有n个关键字信息： (n，P0，K1，P1，K2，P2，......，Kn，Pn)。其中：
          a)   Ki (i=1...n)为关键字，且关键字按顺序升序排序K(i-1)< Ki。 
          b)   Pi为指向子树根的接点，且指针P(i-1)指向子树种所有结点的关键字均小于Ki，但都大于K(i-1)。 
          c)   关键字的个数n必须满足： [ceil(m / 2)-1]<= n <= m-1。如下图所示：

==========================抄录完毕======================

【B树的操作】

B树主要操作有关键字插入，删除关键字，及搜索关键字。这些插入及删除操作执行完毕以后有可能破坏b树的性质，所以必须执行后续调整操作（分裂或者借用或者合并）。

【关键字搜索】

由B树的性质可以知道，我们可以从根节点开始，判断该关键字是否在当前节点---在的话就返回关键字，搜索成功；否则，

举个例子：譬如需要搜索关键字29，从根节点开始，不在根节点，判断29大于17及小于35，那么可以得知必然在根节点的第二个子节点路径上面，找到“26,30”的节点，

不在此节点上，判断29大于26而小于30，那么必然在P2路径上，找到“28,29”，在此节点上面，返回关键字代表的信息。

【关键字的插入】

抄录自july的文章：

 插入一个元素时，首先在B树中是否存在，如果不存在，即在叶子结点处结束，然后在叶子结点中插入该新的元素，注意：如果叶子结点空间足够，这里需要向右移动该叶子结点中大于新插入关键字的元素，如果空间满了以致没有足够的空间去添加新的元素，则将该结点进行“分裂”，将一半数量的关键字元素分裂到新的其相邻右结点中，中间关键字元素上移到父结点中（当然，如果父结点空间满了，也同样需要“分裂”操作），而且当结点中关键元素向右移动了，相关的指针也需要向右移。如果在根结点插入新元素，空间满了，则进行分裂操作，这样原来的根结点中的中间关键字元素向上移动到新的根结点中，因此导致树的高度增加一层。如下图所示：

1、OK，下面咱们通过一个实例来逐步讲解下。插入以下字符字母到一棵空的B 树中（非根结点关键字数小了（小于2个）就合并，大了（超过4个）就分裂）：C N G A H E K Q M F W L T Z D P R X Y S，首先，结点空间足够，4个字母插入相同的结点中，如下图：

 

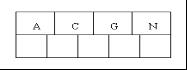
2、当咱们试着插入H时，结点发现空间不够，以致将其分裂成2个结点，移动中间元素G上移到新的根结点中，在实现过程中，咱们把A和C留在当前结点中，而H和N放置新的其右邻居结点中。如下图：

 

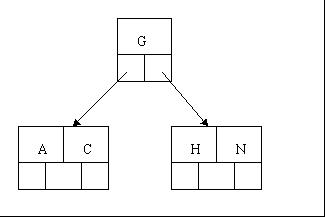
3、当咱们插入E,K,Q时，不需要任何分裂操作

 

 

 

 

 

 

 

 

 

 

 

 

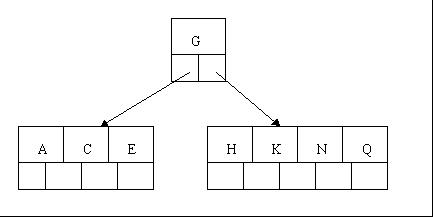
4、插入M需要一次分裂，注意M恰好是中间关键字元素，以致向上移到父节点中

 

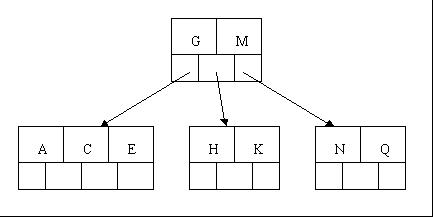
5、插入F,W,L,T不需要任何分裂操作

 

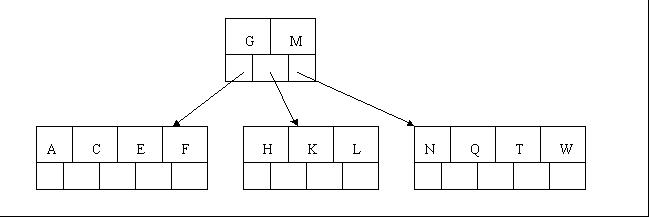
6、插入Z时，最右的叶子结点空间满了，需要进行分裂操作，中间元素T上移到父节点中，注意通过上移中间元素，树最终还是保持平衡，分裂结果的结点存在2个关键字元素。

 

7、插入D时，导致最左边的叶子结点被分裂，D恰好也是中间元素，上移到父节点中，然后字母P,R,X,Y陆续插入不需要任何分裂操作（别忘了，树中至多5个孩子）。

 

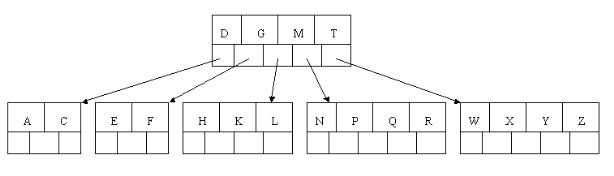
8、最后，当插入S时，含有N,P,Q,R的结点需要分裂，把中间元素Q上移到父节点中，但是情况来了，父节点中空间已经满了，所以也要进行分裂，将父节点中的中间元素M上移到新形成的根结点中，注意以前在父节点中的第三个指针在修改后包括D和G节点中。这样具体插入操作的完成，下面介绍删除操作，删除操作相对于插入操作要考虑的情况多点。

 

=================抄录完毕=====================

备注：

总而言之，首先必须搜寻到需要插入关键字的节点，通常是搜寻该数字最应该存在的叶子节点---假如叶子节点已经有该数字了，那么就返回false。

找到以后按照从小到大的顺序将关键字插入到适合位置，然后看看这个叶子节点的关键字数量是否大于m-1，不大于，不需要调整，大于的话就需要分裂，然后递归处理。

【关键字的删除】

摘抄自 july的部分文章：

首先查找B树中需删除的元素,如果该元素在B树中存在，则将该元素在其结点中进行删除，如果删除该元素后，首先判断该元素是否有左右孩子结点，如果有，则上移孩子结点中的某相近元素(“左孩子最右边的节点”或“右孩子最左边的节点”)到父节点中，然后是移动之后的情况；如果没有，直接删除后，移动之后的情况。

删除元素，移动相应元素之后，如果某结点中元素数目（即关键字数）小于ceil(m/2)-1，则需要看其某相邻兄弟结点是否丰满（结点中元素个数大于ceil(m/2)-1）（还记得第一节中关于B树的第5个特性中的c点么?： c)除根结点之外的结点（包括叶子结点）的关键字的个数n必须满足： （ceil(m / 2)-1）<= n <= m-1。m表示最多含有m个孩子，n表示关键字数。在本小节中举的一颗B树的示例中，关键字数n满足：2<=n<=4），如果丰满，则向父节点借一个元素来满足条件；如果其相邻兄弟都刚脱贫，即借了之后其结点数目小于ceil(m/2)-1，则该结点与其相邻的某一兄弟结点进行“合并”成一个结点，以此来满足条件。那咱们通过下面实例来详细了解吧。

以上述插入操作构造的一棵5阶B树（树中最多含有m（m=5）个孩子，因此关键字数最小为ceil(m / 2)-1=2。还是这句话，关键字数小了（小于2个）就合并，大了（超过4个）就分裂）为例，依次删除H,T,R,E。

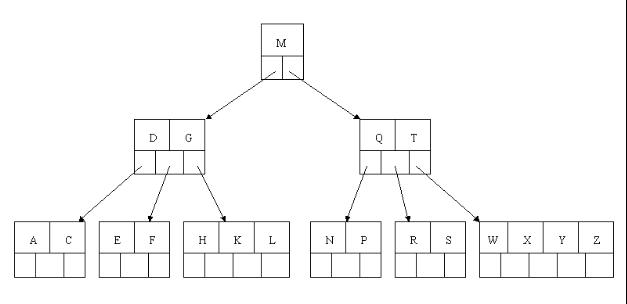
1、首先删除元素H，当然首先查找H，H在一个叶子结点中，且该叶子结点元素数目3大于最小元素数目ceil(m/2)-1=2，则操作很简单，咱们只需要移动K至原来H的位置，移动L至K的位置（也就是结点中删除元素后面的元素向前移动）

 

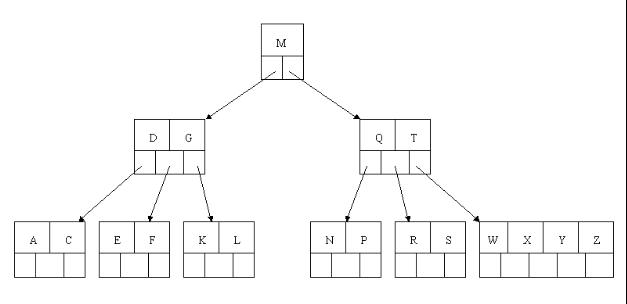
2、下一步，删除T,因为T没有在叶子结点中，而是在中间结点中找到，咱们发现他的继承者W(字母升序的下个元素)，将W上移到T的位置，然后将原包含W的孩子结点中的W进行删除，这里恰好删除W后，该孩子结点中元素个数大于2，无需进行合并操作。

 

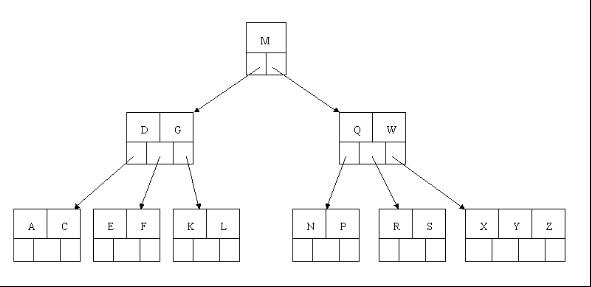
3、下一步删除R，R在叶子结点中,但是该结点中元素数目为2，删除导致只有1个元素，已经小于最小元素数目ceil(5/2)-1=2,而由前面我们已经知道：如果其某个相邻兄弟结点中比较丰满（元素个数大于ceil(5/2)-1=2），则可以向父结点借一个元素，然后将最丰满的相邻兄弟结点中上移最后或最前一个元素到父节点中（有没有看到红黑树中左旋操作的影子?），在这个实例中，右相邻兄弟结点中比较丰满（3个元素大于2），所以先向父节点借一个元素W下移到该叶子结点中，代替原来S的位置，S前移；然后X在相邻右兄弟结点中上移到父结点中，最后在相邻右兄弟结点中删除X，后面元素前移。

 

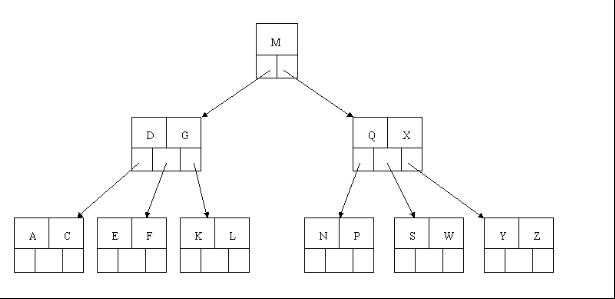
4、最后一步删除E， 删除后会导致很多问题，因为E所在的结点数目刚好达标，刚好满足最小元素个数（ceil(5/2)-1=2）,而相邻的兄弟结点也是同样的情况，删除一个元素都不能满足条件，所以需要该节点与某相邻兄弟结点进行合并操作；首先移动父结点中的元素（该元素在两个需要合并的两个结点元素之间）下移到其子结点中，然后将这两个结点进行合并成一个结点。所以在该实例中，咱们首先将父节点中的元素D下移到已经删除E而只有F的结点中，然后将含有D和F的结点和含有A,C的相邻兄弟结点进行合并成一个结点。

 

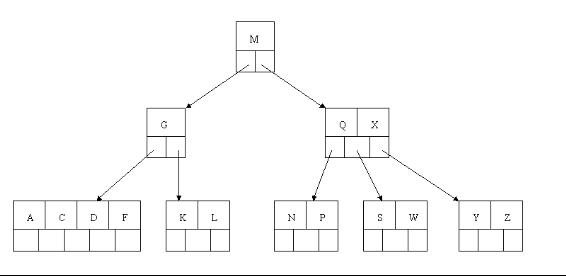
5、也许你认为这样删除操作已经结束了，其实不然，在看看上图，对于这种特殊情况，你立即会发现父节点只包含一个元素G，没达标（因为非根节点包括叶子结点的关键字数n必须满足于2=<n<=4，而此处的n=1），这是不能够接受的。如果这个问题结点的相邻兄弟比较丰满，则可以向父结点借一个元素。假设这时右兄弟结点（含有Q,X）有一个以上的元素（Q右边还有元素），然后咱们将M下移到元素很少的子结点中，将Q上移到M的位置，这时，Q的左子树将变成M的右子树，也就是含有N，P结点被依附在M的右指针上。所以在这个实例中，咱们没有办法去借一个元素，只能与兄弟结点进行合并成一个结点，而根结点中的唯一元素M下移到子结点，这样，树的高度减少一层。

 

为了进一步详细讨论删除的情况，再举另外一个实例：

这里是一棵不同的5序B树，那咱们试着删除C

 

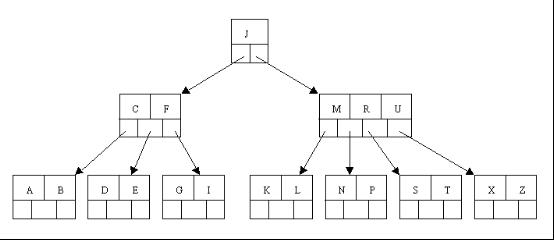
于是将删除元素C的右子结点中的D元素上移到C的位置，但是出现上移元素后，只有一个元素的结点的情况。

又因为含有E的结点，其相邻兄弟结点才刚脱贫（最少元素个数为2），不可能向父节点借元素，所以只能进行合并操作，于是这里将含有A,B的左兄弟结点和含有E的结点进行合并成一个结点。

 

这样又出现只含有一个元素F结点的情况，这时，其相邻的兄弟结点是丰满的（元素个数为3>最小元素个数2），这样就可以想父结点借元素了，把父结点中的J下移到该结点中，相应的如果结点中J后有元素则前移，然后相邻兄弟结点中的第一个元素（或者最后一个元素）上移到父节点中，后面的元素（或者前面的元素）前移（或者后移）；注意含有K，L的结点以前依附在M的左边，现在变为依附在J的右边。这样每个结点都满足B树结构性质。

 

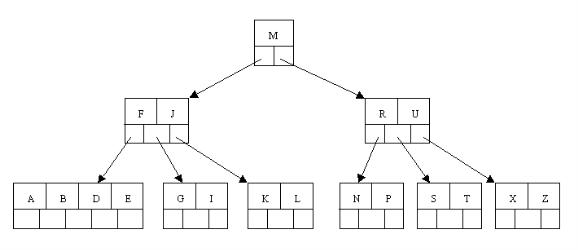
从以上操作可看出：除根结点之外的结点（包括叶子结点）的关键字的个数n满足：（ceil(m / 2)-1）<= n <= m-1，即2<=n<=4。这也佐证了咱们之前的观点。删除操作完。

=============================抄录完毕===================

请注意，删除操作的要点是：可借则借，不可借则并（合并），一旦需要用到合并则必须以父亲作为当前节点再递归调整树形结构。

【B树相关演示程序】

这里设定5阶子树。

【插入关键字9】

【插入关键字12】

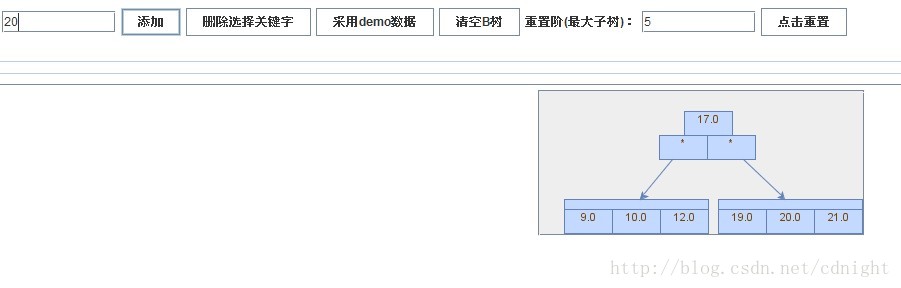
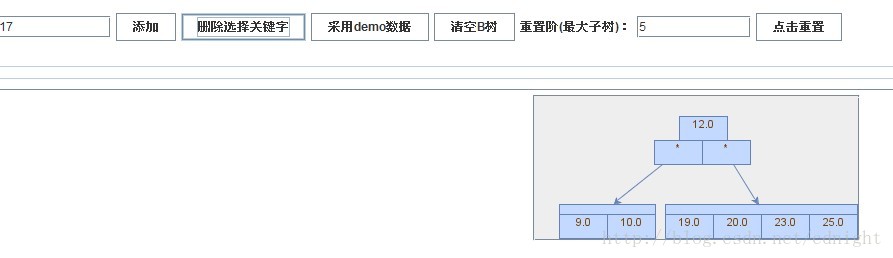
【插入关键字17】

【插入关键字19】

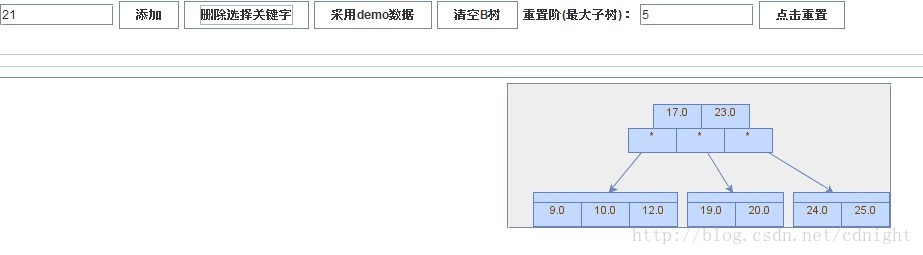
【插入关键字21】

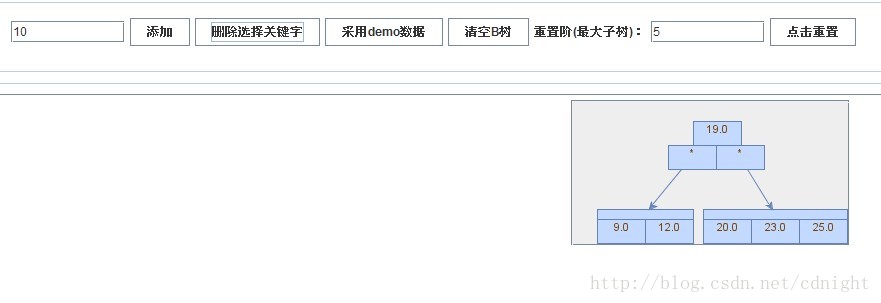
【插入关键字10】

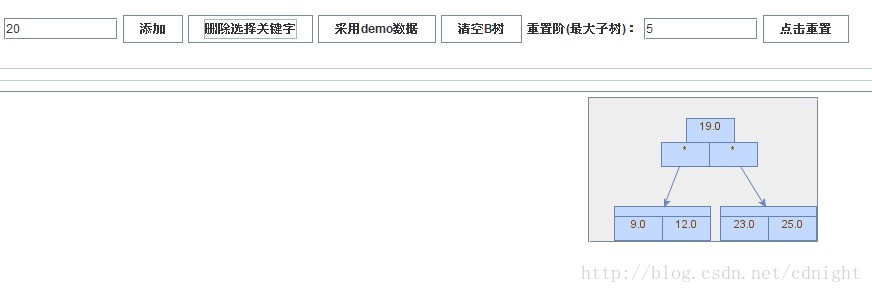
【插入关键字20】

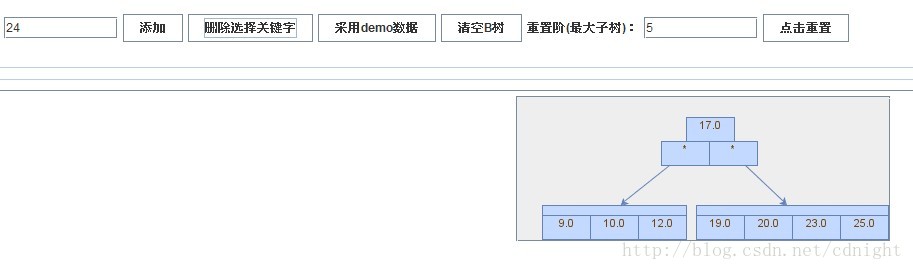
【插入关键字24】

【插入关键字25】

【插入关键字23】

【删除关键字21】

【删除关键字24】

【删除关键字17】

【删除关键字10】

【删除关键字105】

【删除关键字19】

【B树核心代码】

package BTree;public class indexUnit {public  float indexNo;public  Object indexValue=new Object();
}

package BTree;import java.util.ArrayList;public class TreeUnit {public TreeUnit _parent=null;public ArrayList<indexUnit> keys=new ArrayList<indexUnit>();public ArrayList<TreeUnit> childNodes=new ArrayList<TreeUnit>();
}

package BTree;/*** Created with IntelliJ IDEA.* User: Administrator* Date: 13-8-19* Time: 上午10:21* To change this template use File | Settings | File Templates.*/
public class BtreeGen {public TreeUnit _btreeRootNode=new TreeUnit();/** 请注意，这个是最多容纳的子树的阶，b树的阶应该是最多的子树数量，* 根据b树的性质，最大主键数量+1=最多子树数量。* 并且，任何时刻，主键的数量比下属子树数量少1.* */public int _m=6;private int _min=3;public int totalKeys=1;/*** 确定该b树的最大子节点数。* */public BtreeGen(int m){_m=m;_min=(int)Math.ceil((double)m/2);}public boolean insert(float indexNO,Object indexValue){indexUnit iunit=new indexUnit();iunit.indexNo=indexNO;iunit.indexValue=indexValue;TreeUnit needInsertLeaf=recursion_insert_search_leaf_node(indexNO, _btreeRootNode);if(needInsertLeaf==null){//--System.out.println("【警告】找不到需要插入的叶节点！");return false;}else{System.out.println("【提示】需要插入的叶节点为：");for(indexUnit iiUnit:needInsertLeaf.keys){//--System.out.print("  "+iiUnit.indexNo+"  ");}}to_insert(indexNO, indexValue, needInsertLeaf);return true;}private TreeUnit recursion_insert_search_leaf_node(float indexNO,TreeUnit currentUnit){
if(currentUnit==null){return null;
}
//--假如有下属节点，那么就必须跳到下一个点。
if(currentUnit.childNodes.size()>0){int childLoc=0;int cindex=0;for(indexUnit iUnit:currentUnit.keys){if(iUnit.indexNo<indexNO){childLoc=cindex+1;}if(iUnit.indexNo==indexNO){//--已经包含该节点了？那么就返回空，不要再插了。return null;}cindex++;}TreeUnit childTree=currentUnit.childNodes.get(childLoc);return	recursion_insert_search_leaf_node(indexNO, childTree);
}
else{//--没有下属节点，那么就认定是这个叶节点了。return currentUnit;
}}/** 主键的插入。* */
private void to_insert(float indexNO,Object value,TreeUnit currentUnit){int insertLoc=0;for(indexUnit iUnit:currentUnit.keys){if(iUnit.indexNo>indexNO){break;}insertLoc++;}indexUnit insertedUnit=new indexUnit();insertedUnit.indexNo=indexNO;insertedUnit.indexValue=value;currentUnit.keys.add(insertLoc, insertedUnit);if(currentUnit.keys.size()>_m-1){recursion_division(currentUnit);}else{return;}}private void recursion_division(TreeUnit currentUnit){if(currentUnit==null){return;}if(currentUnit.keys.size()<=_m-1){return;}if(currentUnit._parent==null){System.out.println("没有父节点。");TreeUnit leftTree=new TreeUnit();TreeUnit rightTree=new TreeUnit();leftTree._parent=currentUnit;rightTree._parent=currentUnit;indexUnit keyUnit=currentUnit.keys.get(_min-1);int cindex=0;for (indexUnit tmp:currentUnit.keys) {if(cindex<_min-1){leftTree.keys.add(tmp);}else if(cindex>=_min){rightTree.keys.add(tmp);}cindex++;}int theSize=currentUnit.childNodes.size();currentUnit.keys.clear();currentUnit.keys.add(keyUnit);if(currentUnit.childNodes.size()>0){//--for(int ii=0;ii<theSize;ii++){if(ii<=_min-1){currentUnit.childNodes.get(ii)._parent=leftTree;leftTree.childNodes.add(currentUnit.childNodes.get(ii));}else{currentUnit.childNodes.get(ii)._parent=rightTree;rightTree.childNodes.add(currentUnit.childNodes.get(ii));}}}currentUnit.childNodes.clear();currentUnit.childNodes.add(leftTree);currentUnit.childNodes.add(rightTree);return;}System.out.println("父节点不为空。");//--分裂成为了旧节点及新节点两个节点。indexUnit keyUnit=currentUnit.keys.get(_min-1);TreeUnit newTreeUnit=new TreeUnit();newTreeUnit._parent=currentUnit._parent;int cindex=0;for (indexUnit tmp:currentUnit.keys) {if(cindex>=_min){newTreeUnit.keys.add(tmp);}cindex++;}int theSize=currentUnit.keys.size();for(int i2=theSize-1;i2>=_min-1;i2--){currentUnit.keys.remove(i2);}cindex=0;theSize=currentUnit.childNodes.size();for(int ii4=theSize-1;ii4>=_min;ii4--){TreeUnit tmp2=currentUnit.childNodes.get(ii4);tmp2._parent=newTreeUnit;if(newTreeUnit.childNodes.size()<=0){newTreeUnit.childNodes.add(tmp2);}else{newTreeUnit.childNodes.add(0,tmp2);}}for(int ii3=theSize-1;ii3>=_min;ii3--){currentUnit.childNodes.remove(ii3);}int insertPLoc=0;cindex=0;for(indexUnit iUnit:currentUnit._parent.keys){if(iUnit.indexNo<keyUnit.indexNo){insertPLoc=cindex+1;}cindex++;}currentUnit._parent.keys.add(insertPLoc, keyUnit);currentUnit._parent.childNodes.add(insertPLoc+1, newTreeUnit);//--给父节点添加相应子节点。if(currentUnit._parent.keys.size()>_m-1){recursion_division(currentUnit._parent);}return;}public indexUnit search(float indexNO){_searchResultUnit=null;recursion_search(_btreeRootNode,indexNO);return _searchResultUnit;}private indexUnit _searchResultUnit=null;private void recursion_search(TreeUnit currentUnit, float indexNO){if(currentUnit==null){_searchResultUnit=null;return;}for(indexUnit f1:currentUnit.keys){if(f1.indexNo==indexNO){_searchResultUnit=f1;return;}}//--假如上面都找不到，并且该节点下面没有子树了，那么就表示没有这个东西。if(currentUnit.childNodes.size()<=0){return;}int childTreeIndex=0;int ccIndex=0;for(indexUnit f2:currentUnit.keys){if(f2.indexNo<indexNO){childTreeIndex=ccIndex+1;}ccIndex++;}TreeUnit childTreeUnit=currentUnit.childNodes.get(childTreeIndex);recursion_search(childTreeUnit, indexNO);}private TreeUnit _result_treeUnit=null;/*** 获取indexNO所在的节点。* */public TreeUnit getSearchNode(float indexNO){_result_treeUnit=null;recursion_search_node(_btreeRootNode, indexNO);return _result_treeUnit;}/***搜查indexNO所在的节点。* */private void recursion_search_node(TreeUnit treeUnit,float indexNO){if(treeUnit==null){return;}int childChosenIndex=0;int cindex=0;for(indexUnit iTMP:treeUnit.keys){if(indexNO>iTMP.indexNo){childChosenIndex=cindex+1;}if(iTMP.indexNo==indexNO){_result_treeUnit=treeUnit;return;}cindex++;}if(treeUnit.childNodes.size()<=0){return;}//--假如有下面并且当前没包含相关主键，那么就搜索下面子节点的。TreeUnit childTreeUnit=treeUnit.childNodes.get(childChosenIndex);recursion_search_node(childTreeUnit, indexNO);}public int[] getRoute(float indexNO){return null;}public boolean delete(float indexNO){TreeUnit needDelNode=getSearchNode(indexNO);if(needDelNode==null){return false;}return deleteNode(needDelNode, indexNO);}/*** 删除相关节点。* 删除有几种情况：* 1、假如是叶节点，并且删除以后符合b树的性质，譬如：m=6---最大主键数量为5，最少主键数量为2，叶节点删除主键后，假如关键字数量》=2，那么就完成删除操作，* 否则：* 1、看看有没有左右节点，假如左右节点有空余的关键字，那么就借用相应的关键字，* 假如左右节点的关键字数量都是2，没有空余的，那么只能想父节点借用，并且可能会发生合并操作。** */public boolean deleteNode(TreeUnit needDelNode,float indexNO){//System.out.println("需要删除的节点为："+needDelNode.keys.get(0).indexNo);//--找到当前关键字的在节点里面的位置。int indexLoc=-1;int cindex=0;for(indexUnit iUnit:needDelNode.keys){if(iUnit.indexNo==indexNO){indexLoc=cindex;}cindex++;}if(indexLoc==-1){return false;}    	TreeUnit leftChildNode=null;TreeUnit rightChildNode=null;if(needDelNode.childNodes.size()>0){leftChildNode=needDelNode.childNodes.get(indexLoc);rightChildNode=needDelNode.childNodes.get(indexLoc+1);}/*** 假如关键字所在节点为根节点，并且没有任何下属节点，那么就直接删除好了。* */if(needDelNode._parent==null&&(needDelNode.childNodes==null||needDelNode.childNodes.size()<=0)){needDelNode.keys.remove(indexLoc);return true;}/*** 假如关键字包含子节点，那么就进行相关调整,需要递归调整到叶子节点为止。请注意，现在只是调整调换关键字的数值，并没有删除任何关键字，所以* b树的结构没有破坏。* *//*** a.如果x的左孩子节点存在，x->child[i]，并且x->child[i]的节点关键字个数至少是n个，* 则找到 child[i]中最大的关键字max替换x中删除的关键字，继续递归child[i]删除关键字max。* 这一段话引用自网上，但是我想说，假如该节点不是叶子节点，那么对于该节点的某一个关键字keys[i],* 其左子结点及右子节点child[i]与child[i+1]必然存在----这是b树的基本性质。* */if(needDelNode.childNodes!=null&&needDelNode.childNodes.size()>0){//假如左节点有空余的关键字可以使用（解释：对于6阶b树--最多6个子树，每个节点最少有3棵子树，最多5个节点，最少2个节点，有空余关键字是指关键字数量大于或等于3个）if(leftChildNode!=null&&leftChildNode.keys.size()>=_min){int leftLastIndex=leftChildNode.keys.size()-1;needDelNode.keys.remove(indexLoc);needDelNode.keys.add(indexLoc,leftChildNode.keys.get(leftLastIndex));float indexNO1=needDelNode.keys.get(indexLoc).indexNo;//--递归执行return deleteNode(leftChildNode, indexNO1);}//--假如右侧节点有关键字空余else	if(rightChildNode.keys.size()>=_min){int rightLastIndex=0;needDelNode.keys.remove(indexLoc);needDelNode.keys.add(indexLoc, rightChildNode.keys.get(0));return deleteNode(rightChildNode, rightChildNode.keys.get(0).indexNo);}else{//--假如左右子节点都没有空余节点了，那么只能合并了。leftChildNode.keys.add(needDelNode.keys.get(indexLoc));for(indexUnit iUnit:rightChildNode.keys){leftChildNode.keys.add(iUnit);}for(TreeUnit item1:rightChildNode.childNodes){leftChildNode.childNodes.add(item1);}needDelNode.keys.remove(indexLoc);needDelNode.childNodes.remove(indexLoc+1);//--检查父节点是否符合性质，是否需要回溯合并节点。/*** 请注意：这个地方是造成回溯合并的主要情形。* */recursion_checkCombination(needDelNode);return deleteNode(leftChildNode, indexNO);}}/*** * 假如是叶子节点，那么就执行相关操作。* * */else	if(needDelNode.childNodes==null||needDelNode.childNodes.size()<=0){if(needDelNode.keys.size()>=_min){needDelNode.keys.remove(indexLoc);return true;}//---TreeUnit leftBrother=null;TreeUnit rightBrother=null;TreeUnit parentNode=needDelNode._parent;int childIndexLoc=parentNode.childNodes.indexOf(needDelNode);int keyIndexLoc=-1;if(childIndexLoc==0){rightBrother=parentNode.childNodes.get(1);}else if(childIndexLoc==parentNode.childNodes.size()-1){leftBrother=parentNode.childNodes.get(childIndexLoc-1);}else{leftBrother=parentNode.childNodes.get(childIndexLoc-1);rightBrother=parentNode.childNodes.get(childIndexLoc+1);}//--假如左侧兄弟存在并且有多余节点那么就借用了。if(leftBrother!=null&&leftBrother.keys.size()>=_min){keyIndexLoc=childIndexLoc-1;needDelNode.keys.add(0,parentNode.keys.get(keyIndexLoc));parentNode.keys.remove(keyIndexLoc);parentNode.keys.add(keyIndexLoc,leftBrother.keys.get(leftBrother.keys.size()-1));leftBrother.keys.remove(leftBrother.keys.size()-1);return deleteNode(needDelNode, indexNO);}//右侧兄弟有多余的。else if(rightBrother!=null&&rightBrother.keys.size()>=_min){keyIndexLoc=childIndexLoc;needDelNode.keys.add(parentNode.keys.get(keyIndexLoc));parentNode.keys.add(keyIndexLoc,rightBrother.keys.get(0));parentNode.keys.remove(keyIndexLoc+1);rightBrother.keys.remove(0);///-------------return deleteNode(needDelNode, indexNO);}//--两个兄弟都没有多余的，那么就合并好了。else{if(leftBrother!=null){//leftBrother.keys.add(parentNode.keys.get(keyIndexLoc));keyIndexLoc=childIndexLoc-1;leftBrother.keys.add(parentNode.keys.get(keyIndexLoc));for(indexUnit iUnit:needDelNode.keys){leftBrother.keys.add(iUnit);}parentNode.keys.remove(keyIndexLoc);parentNode.childNodes.remove(keyIndexLoc+1);recursion_checkCombination(parentNode);deleteNode(leftBrother, indexNO);return true;}else if(rightBrother!=null){//needDelNode.keys.remove(indexLoc);keyIndexLoc=childIndexLoc;needDelNode.keys.add(parentNode.keys.get(keyIndexLoc));for(indexUnit iUnit:rightBrother.keys){needDelNode.keys.add(iUnit);}parentNode.keys.remove(keyIndexLoc);parentNode.childNodes.remove(keyIndexLoc+1);recursion_checkCombination(parentNode);deleteNode(needDelNode, indexNO);return true;}else{return false;}}}return true;}private void recursion_checkCombination(TreeUnit currentUnit){if(currentUnit==null){return;}if(currentUnit._parent==null&¤tUnit.childNodes.size()<=1){//假如当前节点为根节点，并且没有关键字，那么根节点丢弃，采用新的根节点。_btreeRootNode=currentUnit.childNodes.get(0);_btreeRootNode._parent=null;return;}//假如当前节点为根节点，并且关键字为一，那么就不管了，符合性质。if(currentUnit._parent==null){return;}if(currentUnit.keys.size()>=_min-1){return;}//假如不为根节点，并且节点的关键字小于_min-1，那么必须再回溯递归合并。/*** 分几种情况，假如左侧子节点有空余关键字，那么从左侧节点借，假如右侧节点有空余关键字，那么从右侧节点借，* 否则两边都没有只能继续递归合并了。* */TreeUnit parentNode=currentUnit._parent;int indexLOC=currentUnit._parent.childNodes.indexOf(currentUnit);    	int keyIndexLOC=-1;int childIndexLOC=indexLOC;TreeUnit leftBrother=null;TreeUnit rightBrother=null;if(parentNode.childNodes.size()==2){if(childIndexLOC==0){rightBrother=parentNode.childNodes.get(1);}else{leftBrother=parentNode.childNodes.get(0);}}else if(parentNode.childNodes.size()>=3){if(childIndexLOC==0){rightBrother=parentNode.childNodes.get(1);}else if(childIndexLOC==parentNode.childNodes.size()-1){leftBrother=parentNode.childNodes.get(childIndexLOC-1);}else{leftBrother=parentNode.childNodes.get(childIndexLOC-1);rightBrother=parentNode.childNodes.get(childIndexLOC+1);}}//--左边兄弟节点有余钱，那么就借。if(leftBrother!=null&&leftBrother.keys.size()>=_min){keyIndexLOC=childIndexLOC-1;currentUnit.keys.add(0, parentNode.keys.get(keyIndexLOC));currentUnit.childNodes.add(0,leftBrother.childNodes.get(leftBrother.childNodes.size()-1));parentNode.keys.remove(keyIndexLOC);parentNode.keys.add(keyIndexLOC,leftBrother.keys.get(leftBrother.keys.size()-1));leftBrother.keys.remove(leftBrother.keys.size()-1);leftBrother.childNodes.remove(leftBrother.childNodes.size()-1);return;    			}//--右边兄弟有余钱，那么就借else if(rightBrother!=null&&rightBrother.keys.size()>=_min){keyIndexLOC=childIndexLOC;currentUnit.keys.add(parentNode.keys.get(keyIndexLOC));currentUnit.childNodes.add(rightBrother.childNodes.get(0));parentNode.keys.remove(keyIndexLOC);parentNode.keys.add(rightBrother.keys.get(0));rightBrother.keys.remove(0);rightBrother.childNodes.remove(0);return;}//--大家都没得借，那么就只能递归合并了。else{//--有左侧兄弟if(leftBrother!=null){keyIndexLOC=childIndexLOC-1;leftBrother.keys.add(parentNode.keys.get(keyIndexLOC));for(indexUnit iUnit:currentUnit.keys){leftBrother.keys.add(iUnit);}for(TreeUnit tUnit:currentUnit.childNodes){leftBrother.childNodes.add(tUnit);tUnit._parent=leftBrother;}parentNode.keys.remove(keyIndexLOC);parentNode.childNodes.remove(keyIndexLOC+1);recursion_checkCombination(parentNode);return;}else{//--有右侧兄弟keyIndexLOC=childIndexLOC;currentUnit.keys.add(parentNode.keys.get(keyIndexLOC));for(indexUnit iUnit:rightBrother.keys){currentUnit.keys.add(iUnit);}for(TreeUnit iUnit:rightBrother.childNodes){currentUnit.childNodes.add(iUnit);iUnit._parent=currentUnit;}parentNode.keys.remove(keyIndexLOC);parentNode.childNodes.remove(keyIndexLOC+1);recursion_checkCombination(parentNode);return;}}    		}}

【B树的demo程序资源】

下载b树演示工具（完善版）