二叉搜索树的概念

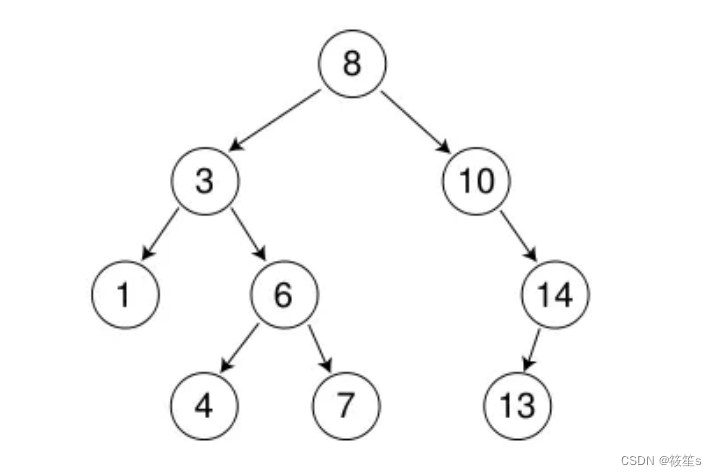
二叉搜索树又称二叉排序树或二叉查找树,它可以是空树,也可以是具备以下性质的二叉树:
1: 若它的左子树不为空,则左子树上所有节点的值都小于根节点的值.

2: 若它的右子树不为空,则右子树上所有节点的值都大于根节点的值.

3: 它的左右子树也分别为二叉搜索树.

注意:
二叉搜索树具备升序和排序的功能.因为根据二叉搜索树的性质,它一般是按照中序遍历的.

二叉搜索树的实现

二叉搜索树的节点

二叉搜索树有三个成员变量分别为: 左指针,右指针,节点值.
为了能够匹配储存多种数据类型,我们选择类模板.

 template < class K >struct BSTreeNode{BSTreeNode<K>* _left;BSTreeNode<K>* _right;K _key;BSTreeNode( const K& key = K() ) //初始化列表:_left(nullptr),_right(nullptr),_key(key)}

构造函数

二查搜索树的成员只有_root根节点,所以只需要对根节点_root构造.

BSTree()
:_root(nullptr)
{
}

注意:
如果我们只写了拷贝构造没写构造函数,此时编译器就不会生成默认构造函数,即使在我们给了缺省值的情况下.

拷贝构造函数

拷贝构造的主要思路就是按照前序遍历的思想,拷贝出一个根节点后依次对它的左子树,右子树进行遍历.

//拷贝构造
BSTree( const BSTree<K>& t )
{_root = _Copy(t._root);
}//拷贝函数
Node* _Copy(Node* root )
{//如果根节点为nulptr,则直接返回到上一层函数栈帧.if( root == nullptr ) {return nullptr;}//遍历左右子树,并与根左右指针建立关系.Node* CopyRoot = new Node(root->_key );CopyRoot->_left = _Copy(root->_left);CopyRoot->_right = _Copy(root->_right);//左右子树递归完毕后返回到第一层函数栈帧.return CopyRoot;}

注意:
因为递归实参要传对象中的private成员,但是在类外却访问不到对象的私密成员,所以在类外我们很难传参.所以在用到递归的函数中,我们都将拷贝构造,插入等成员函数放在private位置,另外我们可以在public位置写一个成员函数来调用对象的内置成员传参,这样可以在类外调用拷贝构造了.(以下成员函数不另作说明)

赋值运算符重载

当我们显示写了拷贝构造就可以考虑现代写法,利用传值传参调用的拷贝构造产生的
BSTree类型的二叉搜索树与旧的二叉搜索树交换_root就行.

BSTree<K>& operator=( BSTree<K> t )
{swap( _root,t._root);return *this;
}

析构函数

二叉搜索树的析构函数本质上是后序遍历,排除root为nullptr后,依次遍历左右子树,再对根节点进行删除.

  ~BSTree()
{_Destroy(_root);  
}
Node* _Destroy( Node*& root )  //为了让形参的改变能影响到实参,故而取引用.
{if( root == nullptr ){return nullptr;    // 返回上一次函数栈帧.}_Destroy(root->_left);_Destroy(root->_right);delete(root);//当根节点删除完毕后,BSTree的_root为空.return nullptr;
}

插入函数

非递归实现

1:　如果为空树,直接在根节点处插入新节点.
　
2:　如果不为空，那么我们便要先查找要插入的位置．
(ａ)：如果所给值key大于该节点值，那么cur就右遍历，并记录当前cur
的parent.
(ｂ)：如果所给值key小于该节点值，那么cur就向左遍历,并记录当前cur的parent.
( c ): 如果所给值key等于该节点值,那么表明插入的节点已经有了,不需要再插入了.

3：然后插入位置后与cur的parent的左右指针建立联系．

bool Insert( const K& key )
{if( _root == nullptr ){_root = new(root);return true;}Node* parent = nullptr;Node* cur = _root;while( cur ){if( cur->_key < key ){parent = cur;cur = cur->_right;}else if( cur->_key > key ){parent = cur;cur = cur->_left;}else                              //相同值插入失败{return false;} }cur = new Node(key);          　//插入key构造的新节点if( parent->_key <　key )      //走到这,parent的左右子树一定为空.{parent->_right = cur;　　　　　                                  //将新节点与parent的右指针相连．}else{parent->_left = cur;}retrn true;
}

递归实现

递归实现本质上类似与前序遍历思想.
1: 如果根为空,就在根处插入新节点.

2: 如果根不为空，比较key与当前节点root的值
( a ):如果key大于当前节点值,就递归root的右子树.
( b ):如果key小于当前节点值,就递归root的左子树．
( c) : 如果key等于当前节点值,就返回错误.(插入失败)

bool _InsertR(Node*& root,const K& key )
{if( root == nullptr){root = new Node(key);return true;}if( root->_key > key ){return _Insert(root->_left,key);}else if( root->_key < key ){return _Insert( root->_right,key);}else{return false;} }

删除函数

非递归实现

查找指定值
二叉搜索树删除时,首先要从根节点循环查找指定值,直到cur为空.
1:如果指定值大于当前结点值,则从当前结点的右子树寻找,并记录当前结点即为父节点.
2: 如果指定值小于当前结点值,则从当前结点的左子树寻找,并记录当前结点即为父节点.
删除指定值
( a )直接删除：
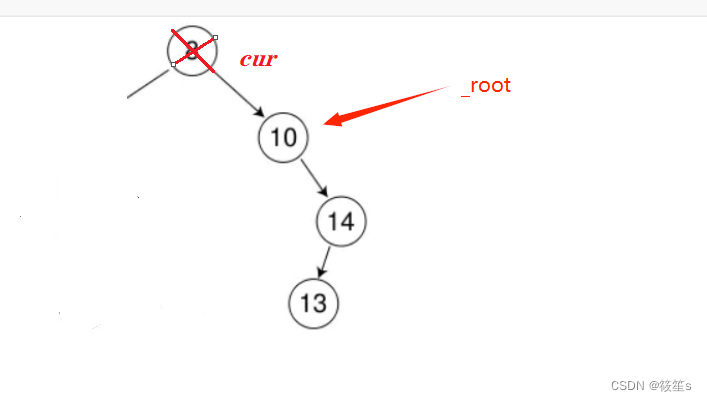
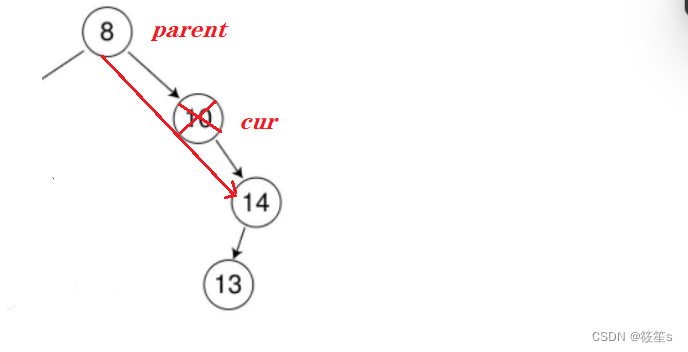
当删除结点只有一个孩子且左为空:
1:如果删除结点cur为根结点,则删除结点的右孩子就为根结点.
2:如果删除结点cur不为根结点,则直接让父结点指向min的右孩子

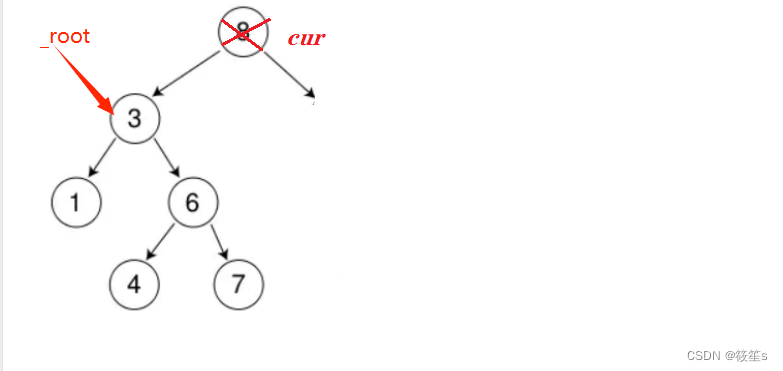
当删除结点只有一个孩子且右为空:
1:如果删除结点cur为根结点,则删除结点的左孩子就为根结点.
2:如果删除结点不为根结点,则直接让父结点指向右孩子

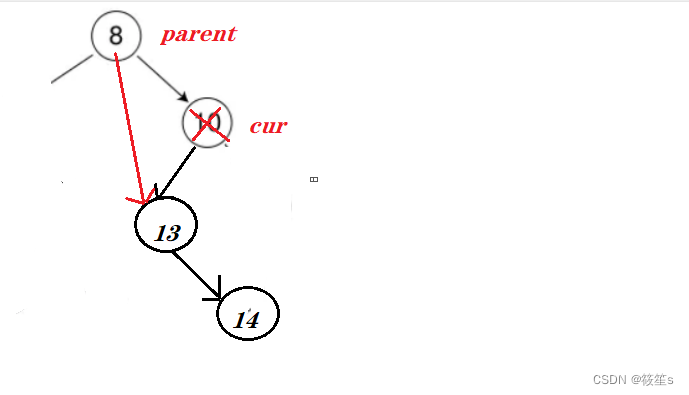
然后根据上述情况直接对删除结点删除．
( b )替换法删除：
当:删除结点左右都不为空，此时便要寻找右子树的最左结点替换结点值后删除，这样删除后可以保持二叉搜索树左子树的结点都比根结点小，右子树的结点都比根结点大的特性．．

注意：
对于替换发删除：
　
（ａ）：寻找右子树的最左结点．用cur记录要删除结点，根据右子树的最左结点必为空的特性下不断向左循环查找，并且我们要记录右子树最左节点的父节点,便于父节点链接最左节点的孩子结点．
（ｂ)：替换删除．在寻找到右子树的最左结点的情况下，我们最终删除的是与cur交换过结点值的替换结点min，但是我们要先确定min结点在minParent的左边还是右边，这样才能方便与min的孩子连接（min的孩子一定为右结点),这种处理同时也包含了min无孩子这一情况.

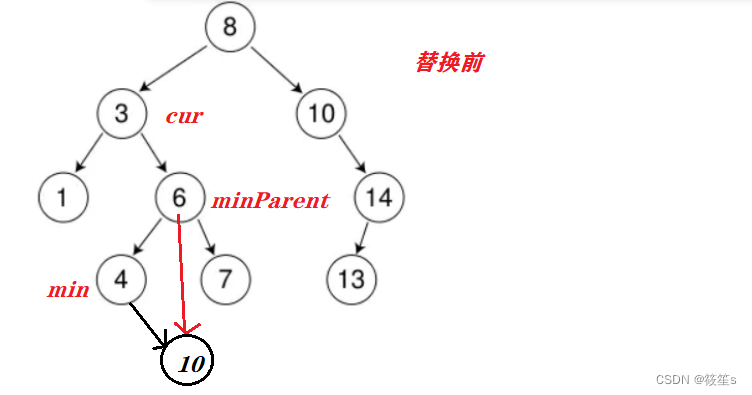
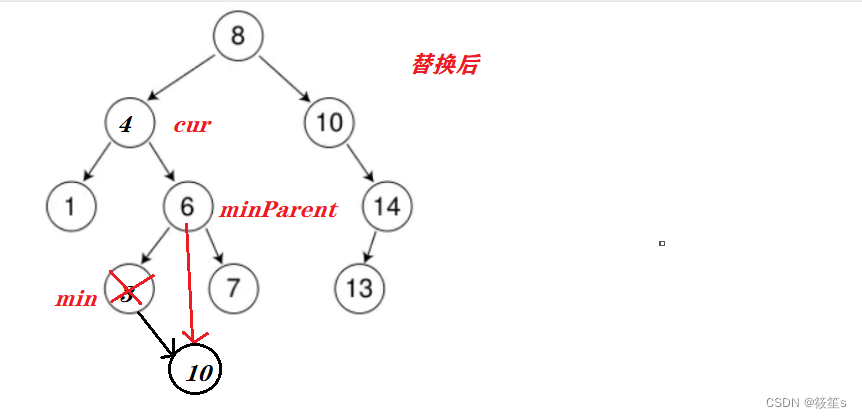
如果min在minParent的左边,则需要将minParent的左指针指向min的右孩子后将cur与min的值替换删除.

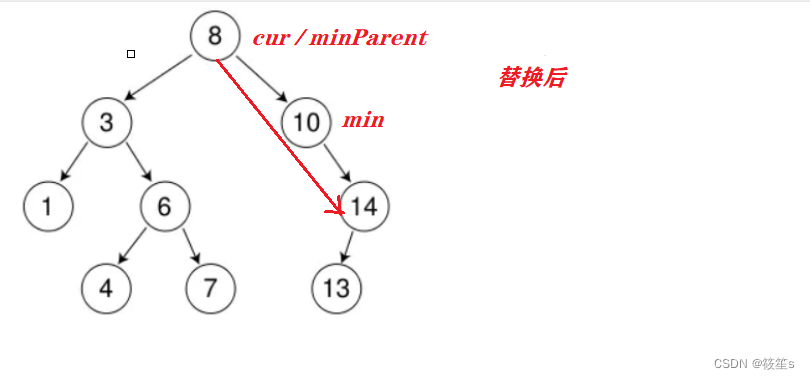
如果min在minParent的右边,及删除结点右子树的最左结点为空的情况下,此时min就是右子树的最左结点,如果minParent初始化为nullptr,则无法进入循环寻找右子树的最左节点,所以可以将minParent初始化为cur.然后将minParent的右指针指向min的右孩子后将cur与min的值替换删除.

重要图示:
min在minParent的左边.

min在minParent的右边;

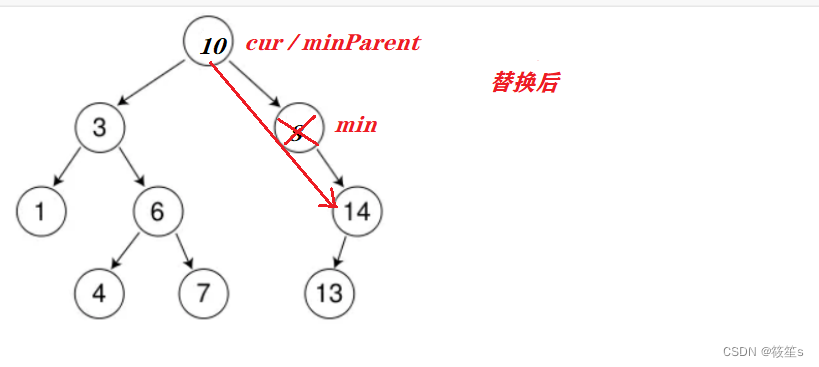
代码实现:

bool Erase( const K& key )
{Node* parent = nullptr;Node* cur = _root;while( cur ){if( cur->_key < key ){parent = cur;cur = cur->_right;}else if( cur->_key > key ){parent = cur;cur = cur->_left;}else                   //找到删除结点{ if( cur->_left == nullptr  ) //当cur的左孩子为空{ if( cur == _root )  //如果删除结点为根结点,则直接让_root指向cur的右孩子{_root = cur->_right;              } else{if( parent->_right == cur ){parent->_right = cur->_right; }else{parent->_left = cur->_right;}}    else if( cur->_right == nullptr )//当cur的右孩子为空{ if( cur == _root ) {_root =　cur->_left;} else {if ( parent->_left == cur  ){     parent->_left = cur->_left;}else{parent->_right = cur->_left;}  }delete cur;       //删除结点return true;  }else            //左右都不为空{//替换法删除//Node* minParent = nullptr; 不能初始化为nullptr;Node* minParent = cur; Node* min =  cur->_right;while( min ->_left ){minParent = min;min = min->_left;    }//判断min在minParent的左边还是右边.if( minParent->_right == min ){minParent->_right = min->_right;}else{minParent->_left = min->_right;}swap( min->_key,cur->_key );delete min;     }  
//走到这里,说明指定结点删除完毕.return true;
}
}
//如果出了循环没有删除,二叉搜索树已经找完了.return false;
}

递归实现

1:首先对空树进行判断,如果为空,则返回false;

2: 根据所给结点值递归查找删除结点.
如果所给值大于当前结点值,就在当前结点的右子树递归查找.
如果所给值小于当前结点值,就在当前结点的左子树递归查找.
3: 删除指定结点
找到删除结点后,此时便要让删除结点父节点与删除节点孩子连接,此时有两种综合情况:
( a ):当删除结点只有一个孩子的情况下:
如果删除结点只有左孩子,则删除结点的父结点与删除结点左孩子连接.
如果删除结点只有右孩子,则删除结点的父节点与删除结点右孩子连接.
( b ): 当删除结点左右孩子都存在:
从删除结点的右子树的最左结点寻找替换点.
交换删除结点与替换点min,从删除结点的右子树递归删除.

//针对递归,公有成员函数调用私有
bool EraseR( const K& key )
{return _EraseR(_root,key );
}bool _EraseR( Node*& root,const K& key )
{     //寻找删除结点if( root == nullptr ){ return false;}if(　root->_key < key ){ return _EraseR( root->_right,key );}else if( root -> _key > key ){return _EraseR ( root->_left,key);}else  //找到了,连接关系后删除{Node* del = root;if( root->_left == nullptr ){root = root->_right;  //此时的root实际上是删除结点父节点的右指针.}else if ( root->_right == nullptr ){ root = root->_left;  //此时root实际上是删除结点父节点的左指针.}else{Node* min = root->_right;while( min->_left )  //从右子树的最左结点开始寻找.{min = min->left;                }//走到这,说明已经找到了替换点.swap(root->_key,min->_key );//替换完成后,此时要删除替换点,再次复用递归.return _EraseR( root->_right,key );               }delete del;return true;}}

注意:
在找到替换结点(min)后,由于替换结点min的左孩子必为nullptr,所以再度递归EraseR时,编译器就不会再度走删除

查找函数

非递归实现

非递归查找与插入前的查找几乎一致：

bool Find(const K& key){Node* cur = _root;//如果二叉树不为空的情况下。while (cur){if (cur->_key < key){//parent = cur;cur = cur->_right;}else if (cur->_key > key){//parent = cur;cur = cur->_left;}//找到相等的，return true就行。。else{return true;}}//在循环里都没找到，说明找不到了。return false;}

递归实现

1: 如果为空,则返回false;

2: 如果指定值大于当前结点值,则递归从前结点的右子树寻找.

3: 如果指定值小于当前结点值的,则递从当前结点的左子树寻找.

4: 如果直接值等于当前结点值,就说明查找值已经找到了,返回true.

bool  FindR( const K& key )
{return _FindR( _root,key );
}bool _FindR( Node* root, const K& key )
{if( root = nullptr ){return false;}if( root->_key < key )　//递归从右子树开始查找{return _FindR( root->right,key );}else if ( root->_key > key ) //递归从左子树开始查找{ return _FindR( root->_left,key );}else       //走到这说明找到了．{return true;}}

二叉搜索树的性能分析

最优情况下，二叉搜索树为完全二叉树（或者接近为完全二叉树），时间复杂度为log2N.

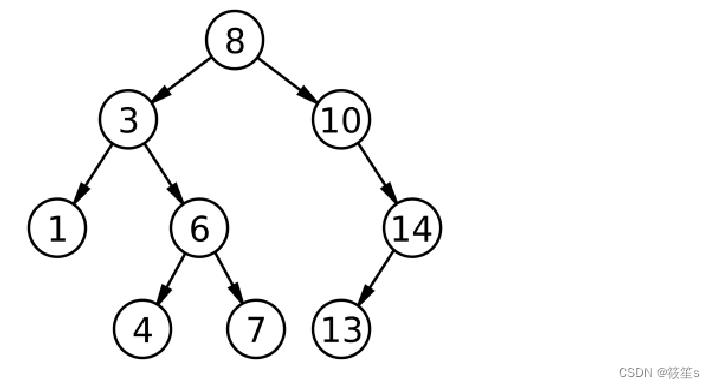
最差情况下,二叉搜索树退化为单支树(或者为单支) ,时间复杂度为O(N);

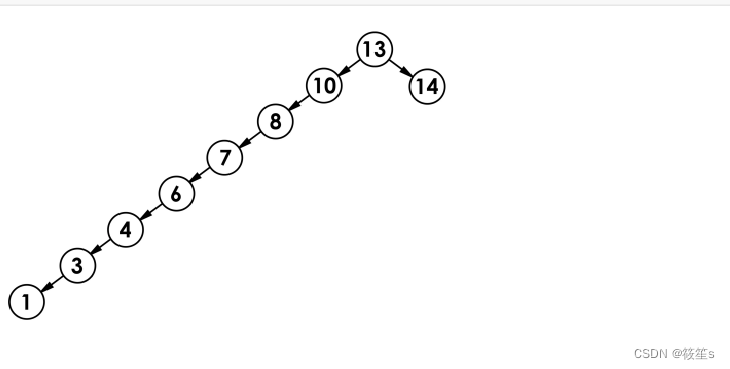
二叉搜索树的完整代码

struct BSTreeNode
{BSTreeNode<K>* _left;BSTreeNode<K>* _right;K _key;BSTreeNode(const K& key):_left(nullptr), _right(nullptr), _key(key){}
};
template<class K>
class BSTree
{typedef BSTreeNode<K> Node;
public://注意，如果写了拷贝构造的话，编译器就不会主动生成默认构造函数，而我们有没有写，这是就会没有合适的默认构造，即使我们//在内置成员给上缺省值。BSTree(){}//拷贝构造BSTree(const BSTree<K>& t){_root = _Copy(t._root);}//析构~BSTree(){_Destroy(_root);}bool Inseret(const K& key){if (_root == nullptr){_root = new Node(key);return true; }Node* parent = nullptr;Node* cur = _root;//如果二叉树不为空的情况下。while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}//插入的值已经有了，就不会插入了。else{return false;}}//找到之后new一个结点给它,可是在插入一个数之后，除了函数作用域cur就被销毁了，编译器找不到//这个结点了，所以链式结构，我们还得找到这个空的父亲的位置。cur = new Node(key);if( parent->_key < key ){parent->_right = cur;}else{parent->_left = cur;}return true;}bool Find(const K& key){Node* cur = _root;//如果二叉树不为空的情况下。while (cur){if (cur->_key < key){//parent = cur;cur = cur->_right;}else if (cur->_key > key){//parent = cur;cur = cur->_left;}//找到相等的，return true就行。。else{return true;}}//在循环里都没找到，说明找不到了。return false;}bool Erase(const K& key){Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}//找到了，开始删除。else{if (cur->_left == nullptr){//如果删除结点为跟结点if (cur == _root){_root = cur->_right;}else{if (cur == parent->_left){parent->_left = cur->_right;}else{parent->_right = cur->_right;}}//替换后删除delete cur;cur = nullptr;}else if (cur->_right == nullptr){if (cur == _root){_root = cur->_left;}else{if (cur == parent->_right){parent->_right = cur->_left;}else{parent->_left = cur->_left;}}//替换后删除。delete cur;}//删除的结点左右都不为空。//替换法删除。else{//如果设置MinParent的初始值为空的情况下，如果删除的结点的为root，//那么替换点要找右树的最左节点，此时min-left为空，不会进入1循环，//anemic在MinParent->_left会导致访问空指针程序崩溃。Node* MinParent = cur;Node* min = cur->_right;while (min->_left){MinParent = min;min = min->_left;} swap(min->_key, cur->_key);if (MinParent->_left == min){MinParent->_left = min->_right;}else{MinParent->_right = min->_right;}delete min;min = nullptr;}return true;}}return false;}bool FindR( const K& key ){return 	_FindR(_root,key);}bool  InsertR(const K& key){return _InsertR(_root, key);}bool  EraseR(const K& key){return _EraseR(_root, key);}void Inorder(){_Inorder(_root);}//显示写了拷贝构造就可以考虑使用现代写法,//传值传参，t是实参的临时拷贝，此时不需要加const因为临时拷贝对于实参本身没有任何的关系。//此时能加const对于类型，但是赋值过程中const BSTree<int>类型t已经发生改变了，//引用加const除了考虑权限还得考虑是否改变，类型加cosnt只需要考虑拷贝。BSTree<K>& operator=(  BSTree<K> t){swap(_root,t._root);//通过this指针获取BSTree<int>类型。return *this;}private://析构函数//为了让_root=nullptr为空形参改变实参，取引用。Node* _Destroy(Node*& root){//如果root为nullptr；if (root == nullptr){return nullptr;}//如果不为nullptr_Destroy(root->_left);_Destroy(root->_right);delete root;}private:Node* _root = nullptr;//拷贝构造：Node* _Copy(Node* root){if (root == nullptr){return nullptr; }//生成一个结点Node* CopyRoot = new Node(root->_key);//与结点的左右指针建立关系。CopyRoot->_left = _Copy(root->_left);CopyRoot->_right = _Copy(root->_right);return CopyRoot;}//查找的非递归玩法。bool _FindR(Node* root, const K& key){if (root == nullptr){return false;}if (root->_key < key){return  _FindR(root->_right, key);}else if (root->_key > key){return _FindR(root->_left, key);}//走到这，说明找到了else{return true;}}//删除的Erase玩法：bool _EraseR(Node*& root, const K& key){if (root == nullptr){return false;}//删除前先判断值的大小，以便确定删除的位置。if (root->_key < key){return _EraseR(root->_right,key);}else if (root->_key > key){return _EraseR(root->_left,key);}//如果相等就说明找到了，删除。else{Node* del = root;if (root->_left == nullptr){//与被删除的结点建立关系。root = root->_right;}else if (root->_right == nullptr) {    //与被删除的结点建立关系。root = root-> _left;}//删除的第三种情况，删除结点的_left和_right都不为nullptr问题。else{//寻找替换点,在右树的最左节点中寻找。Node* min = root->_right;  while (min->_left){min = min->_left;}//跳出来，说明已经找到了。swap(root->_key, min->_key);//转换为在root的右子树进行递归删除。return _EraseR(root->_right, key);}delete del;return true;}}//插入的递归玩法：bool _InsertR(Node*& root, const K& key){//找到了。if (root == nullptr){root = new Node(key);return;}if (root->_key < key){return _InsertR(root->_right, key);}else if (root->_key > key){return _Insert(root->_left, key);}else{return false;}}void _Inorder(Node* root){if (root == nullptr){return;}_Inorder(root->_left);cout << root->_key << " ";_Inorder(root->_right);}};