序言

解答以下的几个困惑：

• 不知道整么想
• 不知道整么做
• 不知道要注意些什么

稍微整理了一下，发现要搞懂的题目特别多，就收缩边界，不要展开，刷完leedcode前300道题，剩下的听天由命。

像 背单词⼀样背算法，对于各种算法技巧，如果没事⼉就看，哪有记不住的道理。

如果看了题 ⽬不能迅速想到解题思路，或者看了思路写不出代码，那就说明这块知识点掌握的不太好，需要重新复习巩固。

TODO : 每个框架10个题默写3遍

背包问题

背包问题专辑

排序

堆排序

//先写出一个节点的堆化操作，再遍历每个节点实现堆化，输出的话就是用最后一个节点替换第一个节点，再堆化。这需要一个过程
func SortArray() []int {arr := []int{6, 3, 5, 4, 1, 2, 7}build(arr)var res []intfor len(arr) != 0 {res = append(res, arr[0])arr[0] = arr[len(arr)-1]arr = arr[:len(arr)-1]build(arr)}fmt.Println(res)return res
}func build(arr []int) {for i := len(arr) - 1; i >= 0; i-- {heapfy(arr, i)}
}func heapfy(nums []int, index int) {if index == len(nums) || (2*index+1) >= len(nums) {return}if (2*index + 2) >= len(nums) {if nums[2*index+1] < nums[index] {swap(nums, 2*index+1, index)}return}root := indexleft := 2*index + 1right := 2*index + 2rootV := nums[root]leftV := nums[left]rightV := nums[right]minV := rootVif leftV < minV {minV = leftVswap(nums, left, root)if left < len(nums) {heapfy(nums, left)}}if rightV < minV {minV = rightVswap(nums, right, root)if right < len(nums) {heapfy(nums, right)}}return
}func swap(nums []int, x, y int) {temp := nums[x]nums[x] = nums[y]nums[y] = temp
}

堆排序：
力扣上能过

func sortArray(nums []int) []int {// 堆排序-大根堆，升序排序，基于比较交换的不稳定算法，时间O(nlogn)，空间O(1)-迭代建堆// 遍历元素时间O(n)，堆化时间O(logn)，开始建堆次数多些，后面次数少 // 主要思路：// 1.建堆，从非叶子节点开始依次堆化，注意逆序，从下往上堆化// 建堆流程：父节点与子节点比较，子节点大则交换父子节点，父节点索引更新为子节点，循环操作// 2.尾部遍历操作，弹出元素，再次堆化// 弹出元素排序流程：从最后节点开始，交换头尾元素，由于弹出，end--，再次对剩余数组元素建堆，循环操作// 建堆函数，堆化var heapify func(nums []int, root, end int)heapify = func(nums []int, root, end int) {// 大顶堆堆化，堆顶值小一直下沉for {// 左孩子节点索引child := root*2 + 1// 越界跳出if child > end {return}// 比较左右孩子，取大值，否则child不用++if child < end && nums[child] <= nums[child+1] {child++}// 如果父节点已经大于左右孩子大值，已堆化if nums[root] > nums[child] {return}// 孩子节点大值上冒nums[root], nums[child] = nums[child], nums[root]// 更新父节点到子节点，继续往下比较，不断下沉root = child}}end := len(nums)-1// 从最后一个非叶子节点开始堆化for i:=end/2;i>=0;i-- {heapify(nums, i, end)}// 依次弹出元素，然后再堆化，相当于依次把最大值放入尾部for i:=end;i>=0;i-- {nums[0], nums[i] = nums[i], nums[0]end--heapify(nums, 0, end)}return nums
}

力扣上超时了

package sortimport "fmt"//堆排序
func main() {arr := []int{1, 9, 10, 30, 2, 5, 45, 8, 63, 234, 12}fmt.Println(HeapSort(arr))
}
func HeapSortMax(arr []int, length int) []int {// length := len(arr)if length <= 1 {return arr}depth := length/2 - 1 //二叉树深度for i := depth; i >= 0; i-- {topmax := i //假定最大的位置就在i的位置leftchild := 2*i + 1rightchild := 2*i + 2if leftchild <= length-1 && arr[leftchild] > arr[topmax] { //防止越过界限topmax = leftchild}if rightchild <= length-1 && arr[rightchild] > arr[topmax] { //防止越过界限topmax = rightchild}if topmax != i {arr[i], arr[topmax] = arr[topmax], arr[i]}}return arr
}
func HeapSort(arr []int) []int {length := len(arr)for i := 0; i < length; i++ {lastlen := length - iHeapSortMax(arr, lastlen)if i < length {arr[0], arr[lastlen-1] = arr[lastlen-1], arr[0]}}return arr
}

多线程

leedcode多线程9道题

• 实现1到100的累加求和

  public static void main(String[] args) throws Exception {AtomicInteger count = new AtomicInteger();for (int i = 1; i <= 10; i++) {int finalI = i;Thread thread = new Thread(() -> {for (int j = (finalI - 1) * 10 + 1; j <= finalI * 10; j++) {count.addAndGet(j);}});thread.start();thread.join();//join必须在start后⾯；join将两个交替执⾏的线程强制为按顺序执⾏。可以说将并⾏的改 成了串⾏}//结果正确5050}System.out.println(count.get());}

数据结构设计(LRU.LFU要求熟练背诵并默认)

LRU

LRU是从时间维度进行淘汰

// 错误设计1：list是拿不到当前节点的引用的
package mainimport ("container/list""fmt"
)func main() {obj := Constructor(2)obj.Put(1, 1)obj.Put(2, 2)fmt.Println(obj.Get(1)) //2obj.Put(3, 3)fmt.Println(obj.Get(2)) //3obj.Put(4, 4)fmt.Println(obj.Get(1)) //4fmt.Println(obj.Get(3)) //4fmt.Println(obj.Get(4)) //4}type LRUCache struct {capacity intsize     intcache    map[int]*list.Listque      *list.List
}type node struct {key, value int
}func Constructor(capacity int) LRUCache {return LRUCache{capacity: capacity,cache:    make(map[int]*list.List),que:      list.New(),}
}func (this *LRUCache) Get(key int) int {if v, ok := this.cache[key]; ok {this.que.MoveBefore(v.Front(), this.que.Front())return (v.Front().Value).(node).value}return -1
}func (this *LRUCache) Put(key int, value int) {if v, ok := this.cache[key]; ok {this.que.MoveBefore(v.Front(), this.que.Front())} else {if this.size+1 > this.capacity {//满了this.que.Remove(this.que.Back())delete(this.cache, key)nd := node{key:   key,value: value,}this.que.PushFront(nd)this.cache[key] = this.que} else {nd := node{key:   key,value: value,}this.que.PushFront(nd)this.cache[key] = this.que/**我依次put了1，2，3我希望的this.cache[key] = this.que是1-2-3 实际 1-2-32-3   实际 1-2-33     实际 1-2-3*/this.size++}}
}

修正后的正确设计–基于golang的list.List双链表，它的remove是O（1），不像linkednode是O（n）

type LRUCache struct {size     intcapacity intque      *list.Listcache    map[int]*list.Element
}type Node struct {key   intvalue int
}func Constructor(capacity int) LRUCache {cache := LRUCache{size:     0,capacity: capacity,cache:    make(map[int]*list.Element),que:      list.New(),}return cache
}func (this *LRUCache) Get(key int) int {if v, ok := this.cache[key]; ok {/**this.que.Remove(v)node := v.Value.(Node)push进去的是Node，那么下文取出来时Value.(*Node)就会报错，必须推进去是list.Elementthis.que.PushFront(node) */this.que.MoveToFront(v)return v.Value.(*Node).value}return -1
}func (this *LRUCache) Put(key int, value int) {if v, ok := this.cache[key]; ok {v.Value.(*Node).value = valuethis.que.MoveToFront(v)} else {if this.size == this.capacity {//满了back := this.que.Back()delete(this.cache, back.Value.(*Node).key)this.que.Remove(back)this.size--}front := this.que.PushFront(&Node{key:   key,value: value,})this.cache[key] = frontthis.size++}
}

不符合时间复杂度的设计-java lineknode

// 不符合时间复杂度的设计2：lineknode的remove在改场景该用法的使用下时间复杂度是O(n)
class LRUCache {private int capacity;private Map<Integer, Integer> cache;private LinkedList<Integer> link;public LRUCache(int capacity) {this.capacity = capacity;cache = new HashMap<>();link = new LinkedList<>();}public int get(int key) {if (!cache.containsKey(key)) return -1;else {int value = cache.get(key);link.remove(Integer.valueOf(key));link.addFirst(key);return value;}}public void put(int key, int value) {if (capacity == 0) return;if (cache.containsKey(key)) {  //k存在，更新缓存kvcache.put(key, value);link.remove(Integer.valueOf(key));link.addFirst(key);} else {if (link.size() == capacity) {cache.remove(Integer.valueOf(link.pollLast()));}link.addFirst(key);cache.put(key, value);}}
}

自定义双链表的正确的LRU实现

type LRUCache struct {size     intcapacity intcache    map[int]*DLinkedNode//双链表的经典实现，记录头节点和尾节点，并且头节点和尾节点都是虚拟哑结点(能极大简化链表的操作)//双链表用空间换时间，可实现删除是O(1)head, tail *DLinkedNode
}type DLinkedNode struct {key        intvalue      intprev, next *DLinkedNode
}func initDLinkedNode(key, value int) *DLinkedNode {return &DLinkedNode{key:   key,value: value,}
}
func Constructor(capacity int) LRUCache {cache := LRUCache{size:     0,capacity: capacity,cache:    make(map[int]*DLinkedNode),// 双链表的构造非常巧妙，初始化首尾2个哑结点head: initDLinkedNode(0, 0),tail: initDLinkedNode(0, 0),}cache.head.next = cache.tailcache.tail.prev = cache.headreturn cache
}func (this *LRUCache) Get(key int) int {if v, ok := this.cache[key]; ok {val := v.valuethis.moveToHead(v)return val}return -1
}func (this *LRUCache) Put(key int, value int) {if v, ok := this.cache[key]; ok {//this.moveToHead(v)  //假设已有3,1，现在用户更新成了3,5，所以这个不能省v.value = valuev.value = valuethis.moveToHead(v)} else {if this.size == this.capacity {//满了tail := this.removeTail()//删除的是key，不是value，不要写成tail.value，这里非常容易不动脑子的写成valuedelete(this.cache, tail.key) this.size--}node := initDLinkedNode(key, value)this.addToHead(node)this.cache[key] = nodethis.size++}
}func (this *LRUCache) addToHead(node *DLinkedNode) {/**this.head.next = nodenode.prev = this.headthis.head.next.prev = node//this.tail.prev = node //写错了，正确写法见上node.next = this.head.next//node.next = this.tail //写错了，正确写法见上*/node.prev = this.headnode.next = this.head.nextthis.head.next.prev = nodethis.head.next = node}func (this *LRUCache) removeNode(node *DLinkedNode) {/**错误写法p := node.prevn := node.nextn.next = pp.next = n*/node.prev.next = node.nextnode.next.prev = node.prev
}func (this *LRUCache) moveToHead(node *DLinkedNode) {//先移除节点，在添加到头部，非常妙，简化了移动指针的很复杂的操作this.removeNode(node)this.addToHead(node)
}func (this *LRUCache) removeTail() *DLinkedNode {prev := this.tail.prevthis.removeNode(prev)return prev
}

LFU

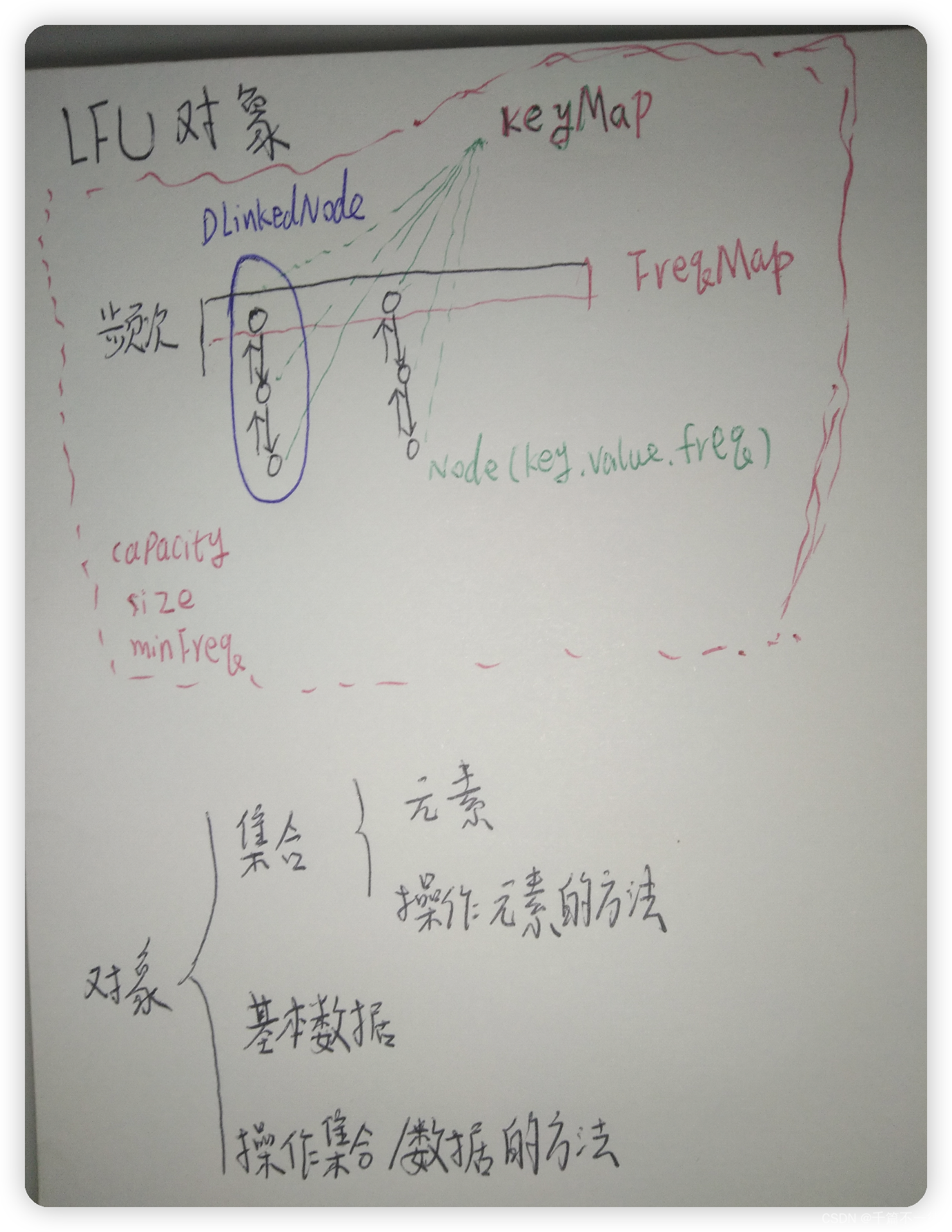
LFU根据使用频次进行淘汰-同频再根据时间淘汰

type LFUCache struct {minFreq   intsize      intcapacity  intfreqTable map[int]*DLinkedNodekeyTable  map[int]*Node
}func Constructor(capacity int) LFUCache {cache := LFUCache{size:      0,capacity:  capacity,freqTable: make(map[int]*DLinkedNode),keyTable:  make(map[int]*Node),minFreq:   0,}return cache
}func (this *LFUCache) Get(key int) int {if val, ok := this.keyTable[key]; ok {value := val.valuefreq := val.freqlnode := this.freqTable[freq]lnode.remove(val)delete(this.keyTable,key)aa := this.freqTable[this.minFreq]if aa.head.next == aa.tail {this.minFreq++}if mv, ok := this.freqTable[freq+1]; ok {n :=initNode(key, value, freq+1)mv.addFirst(n)this.keyTable[key]=n} else {lnode := initDLinkedNode()node := initNode(key, value, freq+1)this.keyTable[key] = nodelnode.addFirst(node)this.freqTable[freq+1] = lnode}return value} else {return -1}
}func (this *LFUCache) Put(key int, value int) {if val, ok := this.keyTable[key]; ok {//升级频率freq := val.freqlnode := this.freqTable[freq]lnode.remove(val)aa := this.freqTable[this.minFreq]if aa.head.next == aa.tail {this.minFreq++}if mv, ok := this.freqTable[freq+1]; ok {n := initNode(key, value, freq+1)mv.addFirst(n)this.keyTable[key] = n} else {lnode := initDLinkedNode()node := initNode(key, value, freq+1)this.keyTable[key] = nodelnode.addFirst(node)this.freqTable[freq+1] = lnode}} else {if this.size == this.capacity {if this.capacity == 0 {return} else {prev := this.freqTable[this.minFreq].tail.prevthis.freqTable[this.minFreq].remove(prev)delete(this.keyTable, prev.key)//delete(this.freqTable, this.minFreq) capity容量表示能放多少个key，而不是频次分类的key数量this.size--}}if val, ok := this.freqTable[1]; ok {n := initNode(key, value, 1)val.addFirst(n)this.keyTable[key] = n} else {lnode := initDLinkedNode()node := initNode(key, value, 1)this.keyTable[key] = nodelnode.addFirst(node)this.freqTable[1] = lnode}this.size++this.minFreq = 1}
}type Node struct {key        intvalue      intfreq       intprev, next *Node
}type DLinkedNode struct {head, tail *Node
}func (n DLinkedNode) addFirst(node *Node) {node.next = n.head.nextn.head.next.prev = noden.head.next = nodenode.prev = n.head
}func (n DLinkedNode) remove(val *Node) {nt := val.nextp := val.prevp.next = ntnt.prev = p
}func initDLinkedNode() *DLinkedNode {head := initNode(0, 0, 0)tail := initNode(0, 0, 0)head.next = tailtail.prev = headreturn &DLinkedNode{head: head,tail: tail,}
}func initNode(key, value, freq int) *Node {return &Node{key:   key,value: value,freq:  freq,}
}

红黑树

跳表

练习题

labuldong 的刷题笔记目录

labuldong 的刷题笔记目录

第⼀章、基础数据结构

数组双指针

⼆分搜索

34.在排序数组中查找元素的第⼀个和最后⼀个位置

704. ⼆分查找

35. 搜索插⼊位置

354. 俄罗斯套娃信封问题

392. 判断⼦序列

793. 阶乘函数后 K 个零

875. 爱吃⾹蕉的珂珂

1011. 在 D 天内送达包裹的能⼒

滑动窗⼝

3. ⽆重复字符的最⻓⼦串

76. 最⼩覆盖⼦串

438. 找到字符串中所有字⺟异位词

567. 字符串的排列

239. 滑动窗⼝最⼤值

其他题⽬

26. 删除有序数组中的重复项

27. 移除元素

283. 移动零

259. 较⼩的三数之和

11. 盛最多⽔的容器

42. 接⾬⽔

15. 三数之和

18. 四数之和

1099. ⼩于 K 的两数之和

16. 最接近的三数之和

870. 优势洗牌

986. 区间列表的交集

链表双指针

2. 两数相加

19. 删除链表的倒数第 N 个结点

21. 合并两个有序链表

23. 合并 K 个升序链表

141. 环形链表

142. 环形链表 II

160. 相交链表

876. 链表的中间结点

25. K 个⼀组翻转链表

83. 删除排序链表中的重复元素

92. 反转链表 II

234. 回⽂链表

前缀和

303. 区域和检索 - 数组不可变

304. ⼆维区域和检索 - 矩阵不可变

327. 区间和的个数

1352. 最后 K 个数的乘积

差分数组

370. 区间加法

1094. 拼⻋

1109. 航班预订统计

队列/栈算法

20. 有效的括号

921. 使括号有效的最少添加

1541. 平衡括号字符串的最少插⼊次数

32. 最⻓有效括号

71. 简化路径

150. 逆波兰表达式求值

225. ⽤队列实现栈

232. ⽤栈实现队列

239. 滑动窗⼝最⼤值

⼆叉堆

23. 合并 K 个升序链表

215. 数组中的第 K 个最⼤元素

295. 数据流的中位数

703. 数据流中的第 K ⼤元素

1834. 单线程 CPU

1845. 座位预约管理系统

数据结构设计

146. LRU 缓存机制

341. 扁平化嵌套列表迭代器

380. O(1) 时间插⼊、删除和获取随机元素

460. LFU 缓存

895. 最⼤频率栈

1845. 座位预约管理系统

第⼆章、进阶数据结构

⼆叉树

94. ⼆叉树的中序遍历

100. 相同的树

102. ⼆叉树的层序遍历

103. ⼆叉树的锯⻮形层序遍历

104. ⼆叉树的最⼤深度

144. ⼆叉树的前序遍历

543. ⼆叉树的直径

105. 从前序与中序遍历序列构造⼆叉树

106. 从中序与后序遍历序列构造⼆叉树

654. 最⼤⼆叉树

107. ⼆叉树的层序遍历 II

111. ⼆叉树的最⼩深度

114. ⼆叉树展开为链表

116. 填充每个节点的下⼀个右侧节点指针

226. 翻转⼆叉树

145. ⼆叉树的后序遍历

222. 完全⼆叉树的节点个数

236. ⼆叉树的最近公共祖先

297. ⼆叉树的序列化与反序列化

341. 扁平化嵌套列表迭代器

501. ⼆叉搜索树中的众数

559. N 叉树的最⼤深度

589. N 叉树的前序遍历

590. N 叉树的后序遍历

652. 寻找重复的⼦树

965. 单值⼆叉树

⼆叉搜索树

95. 不同的⼆叉搜索树 II

96. 不同的⼆叉搜索树

98. 验证⼆叉搜索树

450. 删除⼆叉搜索树中的节点

700. ⼆叉搜索树中的搜索

701. ⼆叉搜索树中的插⼊操作

230. ⼆叉搜索树中第 K ⼩的元素

538. 把⼆叉搜索树转换为累加树

1038. 把⼆叉搜索树转换为累加树

501. ⼆叉搜索树中的众数

530. ⼆叉搜索树的最⼩绝对差

783. ⼆叉搜索树节点最⼩距离

1373. ⼆叉搜索⼦树的最⼤键值和 图论算法

图论算法

图的遍历

797. 所有可能的路径

⼆分图

785. 判断⼆分图

886. 可能的⼆分法

环检测/拓扑排序

207. 课程表

210. 课程表 II 并查集算法

765. 情侣牵⼿

130. 被围绕的区域

990. 等式⽅程的可满⾜性

最⼩⽣成树

261. 以图判树

1135. 最低成本联通所有城市

1584. 连接所有点的最⼩费⽤

最短路径

743. ⽹络延迟时间

1514. 概率最⼤的路径

1631. 最⼩体⼒消耗路径

第三章、暴⼒搜索算法

回溯算法

17. 电话号码的字⺟组合

22. 括号⽣成

37. 解数独

39. 组合总和

46. 全排列

77. 组合

78. ⼦集

51. N 皇后

104. ⼆叉树的最⼤深度

494. ⽬标和

698. 划分为 k 个相等的⼦集

DFS 算法

130. 被围绕的区域

200. 岛屿数量

694. 不同的岛屿数量

695. 岛屿的最⼤⾯积

1020. ⻜地的数量

1254. 统计封闭岛屿的数⽬

1905. 统计⼦岛屿

BFS 算法

102. ⼆叉树的层序遍历

103. ⼆叉树的锯⻮形层序遍历

107. ⼆叉树的层序遍历 II

111. ⼆叉树的最⼩深度

752. 打开转盘锁

773. 滑动谜题

第四章、动态规划算法

⼀维 DP

45. 跳跃游戏 II

55. 跳跃游戏

53. 最⼤⼦序和

70. 爬楼梯

198. 打家劫舍

213. 打家劫舍 II

337. 打家劫舍 III

300. 最⻓递增⼦序列

354. 俄罗斯套娃信封问题

322. 零钱兑换

⼆维 DP

10. 正则表达式匹配

62. 不同路径

64. 最⼩路径和

72. 编辑距离

121. 买卖股票的最佳时机

122. 买卖股票的最佳时机 II

123. 买卖股票的最佳时机 III

188. 买卖股票的最佳时机 IV

309. 最佳买卖股票时机含冷冻期

714. 买卖股票的最佳时机含⼿续费

174. 地下城游戏

312. 戳⽓球

416. 分割等和⼦集

494. ⽬标和

514. ⾃由之路

518. 零钱兑换 II

583. 两个字符串的删除操作

712. 两个字符串的最⼩ ASCII 删除和

1143. 最⻓公共⼦序列

787. K 站中转内最便宜的航班

887. 鸡蛋掉落

931. 下降路径最⼩和

背包问题

416. 分割等和⼦集

494. ⽬标和

518. 零钱兑换 II

第五章、其他经典算法

数学算法

17. 电话号码的字⺟组合

77. 组合

78. ⼦集

134. 加油站

136. 只出现⼀次的数字

191. 位 1 的个数

231. 2 的幂

268. 丢失的数字

172. 阶乘后的零

793. 阶乘函数后 K 个零

204. 计数质数

292. Nim 游戏

319. 灯泡开关

877. ⽯⼦游戏

295. 数据流的中位数

372. 超级次⽅

382. 链表随机节点

398. 随机数索引

391. 完美矩形

509. 斐波那契数

645. 错误的集合

710. ⿊名单中的随机数

区间问题

56. 合并区间

986. 区间列表的交集

1288. 删除被覆盖区间

435. ⽆重叠区间

452. ⽤最少数量的箭引爆⽓球

1024. 视频拼接

1834. 单线程 CPU