广告设计公司怎么找业务seo推广优化平台

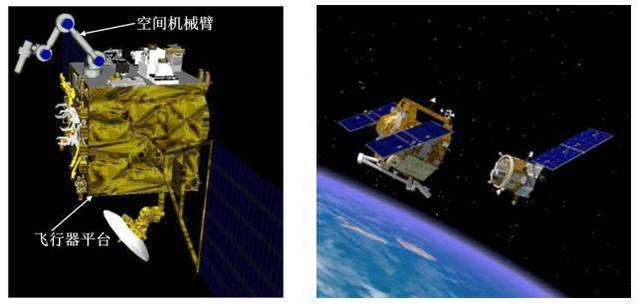
空间机器人笛卡尔路径规划按照路径的性质可以分为笛卡尔点到点的路径规划以及笛卡尔连续路径规划。即通过事先给定空间机器人的目标点或者目标路径，通过运动学的计算得到空间机器人关节层轨迹，进而实现期望路径的跟踪。此外，空间机器人的笛卡尔路径因为参考系的不同可以分为基座连体坐标系下的路径跟踪以及惯性坐标系下的路径跟踪。

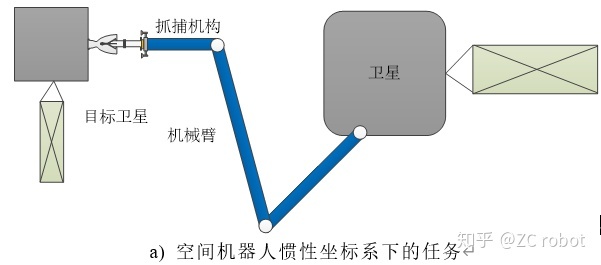
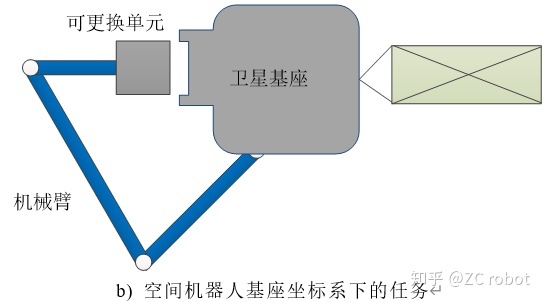
如上图，在卫星基座坐标系下的空间机器人末端运动一般用于实现ORU更换、拧螺栓、电器插拔等操作问题，此种方式下机械臂的控制可以类比固定基座机械臂你的控制方法。在惯性坐标系下的空间机器人末端运动一般用于目标捕获等任务，此种情况下机械臂的控制需要考虑到基座的状态。

对于空间机器人的笛卡尔路径规划，一方面，基于GJM的运动规划策略会受到GJM奇异的影响，即惯性系下的某方向上的微小位移将会引起关节空间无限大的速度变化，GJM的奇异不仅与空间机器人系统的运动学参数有关，还涉及到空间机器人系统的动力学参数，因此，GJM的奇异被成为 “动力学奇异”。

另一方面，定义空间机器人所有奇异臂型所对应的笛卡尔空间的点集合成为空间机器人路径相关工作空间PDW(Path Dependent Workspace)，而除此之外的可达工作空间成为空间机器人的路径无关工作空间PIW(Path Independent Workspace)。当机械臂工作在PIW内时，动力学奇异不会发生；当机械臂工作在PDW内时，则有可能会遇到动力学奇异，机械臂遇到动力学奇异，需要及时采取动力学奇异回避的路径规划算法，以防止关节角速度和笛卡尔任务速度的突变。
对于空间机器人点到点的路径规划，由于末端执行器的位置和姿态与当前关节角度以及关节运动历史轨迹有关，学者E. Papadopoulos[[i]]提出一种考虑空间机器人非完整约束特性的点到点路径规划算法，该算法在PIW中找一过渡点，机械臂首先运动到PIW中的过渡点位置，再从过渡点处通过机械臂关机的闭合路径运动调整基座姿态，再从过渡点运动到期望点位置。

S. Pandey和S. Agrawal[[ii]]提出空间机器人”Mode Summation”的路径规划算法。其采用正弦函数对机械臂关节角度进行参数化，进而实现通过机械臂的平动关节的运动控制卫星基座的运动。

R. Lampariello[[iii]]等学者将该方法应用到旋转关节空间机器人，从而使得空间机器人通过机械臂关节的运动可以实现基座姿态调整。

对于空间机器人笛卡尔连续路径规划，其主要是实现末端或者基座跟踪一段连续的路径。其可以分为:基座姿态调整下的笛卡尔连续位置或者姿态跟踪、姿态无扰动的笛卡尔连续位置或者姿态跟踪、笛卡尔连续位置以及姿态跟踪。与空间机器人点到点路径规划不一样的是，对于空间机器人笛卡尔连续路径规划，其需要事先对笛卡尔路径进行规划，任意时刻的轨迹是已知的，且借助于空间机器人逆运动学完成笛卡尔空间任务到关节空间轨迹的转化。

空间机器人实现笛卡尔连续路径跟踪任务，其逆运动学解算至关重要。对于固定基座，其运动学可以分为位置级别逆运动学，速度级别的逆运动学以及加速度级逆运动学。

[[i]] Papadopoulos E G. Path Planning For Space Manipulators Exhibiting Non- holonomic Behavior[C]//IROS. 1992: 669-675.
[[ii]] Pandey S, Agrawal S K. Path planning of free floating prismatic-jointed manipulators [J]. Multibody System Dynamics, 1997, 1(1): 127-140.
[[iii]] Lampariello R, Deutrich K. Simplified path planning for free-floating robots [J]. 1999.