A.数的划分

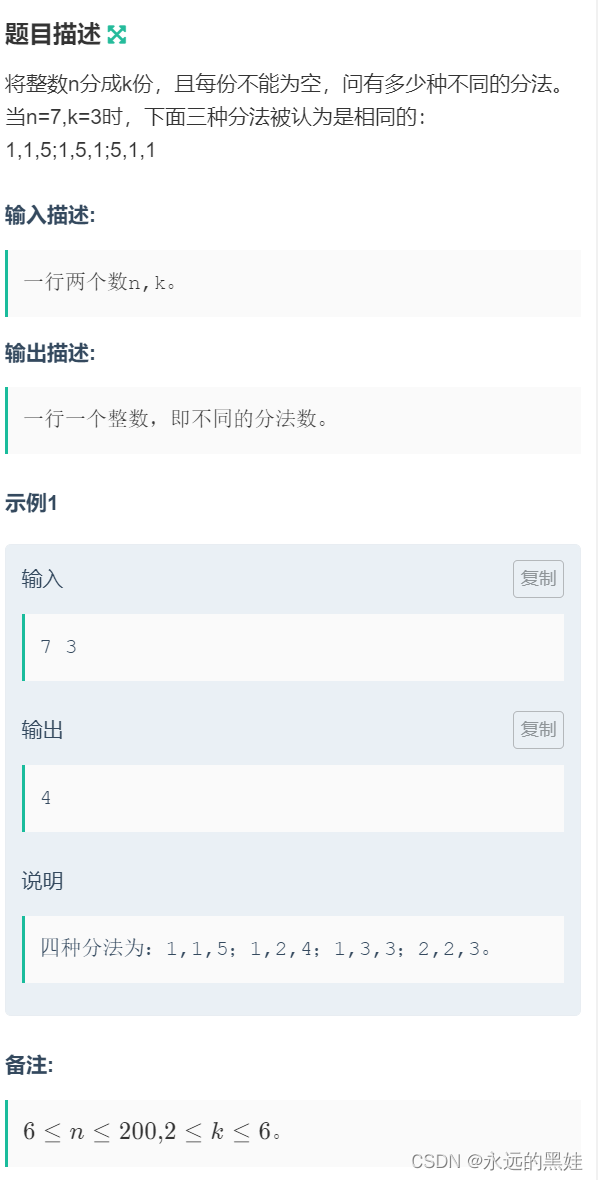
 思路：这道题呢本质上是一个动态规划，转移方程也很简单:

dp[i][j]=dp[i][j-1]+dp[i-j][j];

这里举个例子瞬间理解：

例：dp[3][3]将三分成三部分1，1，1。dp[6][3]为将

六分成三部分，根据状态转移方程dp[6][3]=dp[3][3]+dp[6][2];这里

dp[6][2]是在它的前提下加上一个1值，刚好组合成6，而这时dp[3][3]则是将分成状态的每一个值都加一个1，变成了2，2，2.这部分是难理解的地方。

#include<bits/stdc++.h>
using namespace std;
int dp[1000][1000];
int main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int num1,num2;cin>>num1>>num2;for(int i=1;i<=num1;i++){for(int i1=1;i1<=min(i,num2);i1++){if(i==i1)dp[i][i1]=1;else dp[i][i1]=dp[i-1][i1-1]+dp[i-i1][i1];}}cout<<dp[num1][num2];
}

B.生日蛋糕

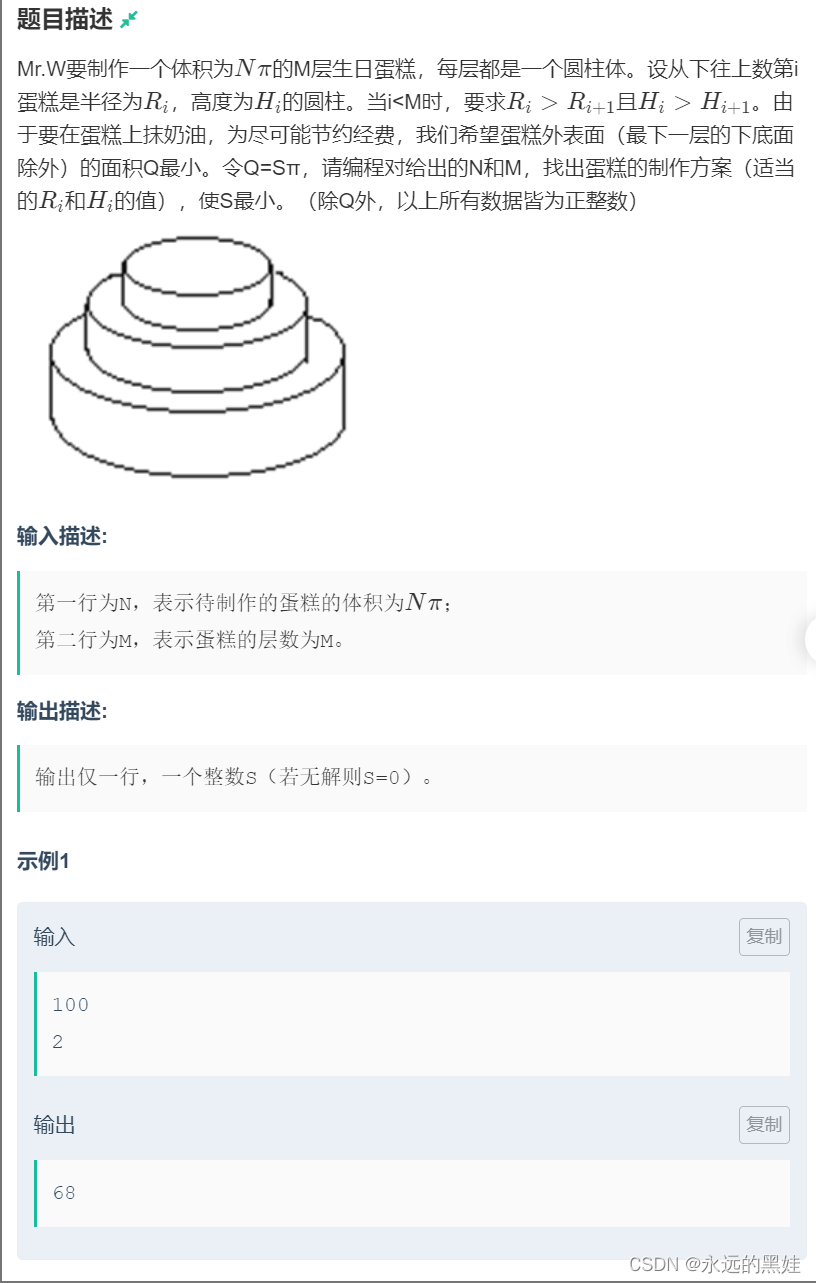
 思路:这道题是一道经典的深搜题型，我们要把最大半径和最大高度，表示出来，已知体积是n,而最大半径就是当高度为1时，所以最大半径可为sqrt(n)，而最大高度为当半径为1时，即为最大高度所以最大高度理所应当为n，(这里题目取消了派值的意义。)我们分别从大到小进行枚举即可。这个我们最先的枚举过程一定要加上底部最大圆的面积，省的我们之后处理，加最大圆的面积之后我们在之后遍历的时候我们只需要加上柱形边缘面积即可。最后遍历到最大层数储存最小值即可。我们这里需要的剪纸技巧是当前总面积数大于储存的最小面积数直接走开即可。还有就是当前的体积加上剩下的最大体积小于要做的蛋糕体积，说明当前枚举的结果太小了，直接返回即可。

#include<bits/stdc++.h>
using namespace std;
const int maxn=1e9;
int n,m;
int ans=maxn;
void dfs(int s,int v,int r,int h,int deep)
{if(ans<s)//剪纸技巧1{return ;}if(r*r*h*(m-deep)+v<n)//剪纸技巧2{return ;}if(v>n)return ;//剪纸技巧3if(v==n&&deep==m)//特判答案{ans=min(ans,s);return ;}for(int i=r-1;i>=m-deep;i--)//持续遍历{for(int i1=h-1;i1>=m-deep;i1--){dfs(2*i*i1+s,i*i*i1+v,i,i1,deep+1);}}
}
int main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin>>n>>m;int maxr=sqrt(n);int maxh=n;for(int i=maxr;i>=1;i--){for(int i1=maxh;i1>=1;i1--){dfs(2*i*i1+i*i,i*i*i1,i,i1,1);//枚举可能出现的所有半径高度情况}}cout<<ans;
}

C.小木棍

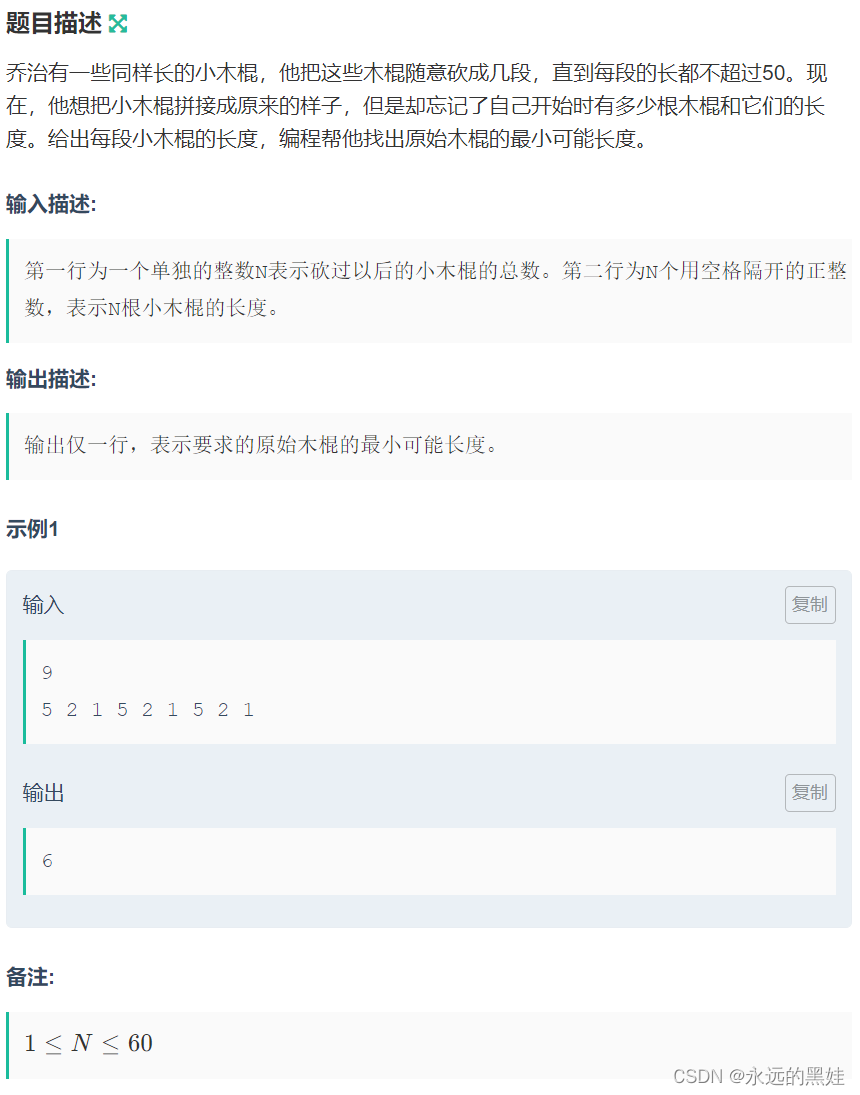
 思路：这道题具体让我们干什么，就是枚举一个数看看这个数是不是所有木棍和的因子，如果是因子的话就看看数列当中的所有数能不能分成对应份数也就是，木棍的数目(木棍的数目等于总长度/因子)。我们将木棍从大到小排，这样遍历的次数会变的很少，既然我们要遍历因子，我们从数列中的最大数开始，到总和的一半，因为一半之后就不存在因子了。在我们dfs过程中我们因为是枚举所有可能所以我们要回溯，结束条件是要求遍历的木棍数目为0的时候，直接程序结束即可。当我们储存的棍子长度等于我们要枚举的木棍长度时，我们将目标数减1，木棍长度为0，继续遍历。剪纸技巧，我们在枚举过程中会遇到相同的木棍，直接调一个next数组即可。当我们的木棍总和减去枚举的当前长度大于数列当中的最大数，直接返回。

#include<bits/stdc++.h>
using namespace std;
int n;
int nex[65];
bool visit[65];
int w[65];
int sums;
void dfs(int index,int sum,int leng,int target)
{if(!target){printf("%d",leng);exit(0);}if(sum==leng){dfs(1,0,leng,target-1);return ;}if(leng-sum<w[n])return ;for(int i=index;i<=n;i++)if(!visit[i]&&sum+w[i]<=leng)//没有被访问过的和加上当前权值一定要小于枚举长度{visit[i]=true;dfs(i+1,sum+w[i],leng,target);visit[i]=false;//回溯if(sum+w[i]==leng||!sum)//满足条件直接返回break;i=nex[i]-1;//到下一个不同的值}
}
int main()
{scanf("%d",&n);for(int i=1;i<=n;i++)scanf("%d",&w[i]),sums+=w[i];sort(w+1,w+1+n,greater<int>());for(int i=1;i<=n;i++)//next数组{int pos=i+1;while(w[i]==w[pos]&&pos<=n)pos++;nex[i]=pos;}for(int i=w[1];i<=sums/2;i++){if(sums%i==0)dfs(1,0,i,sums/i);}printf("%d",sums);return 0;
}

D.Addition Chains

 

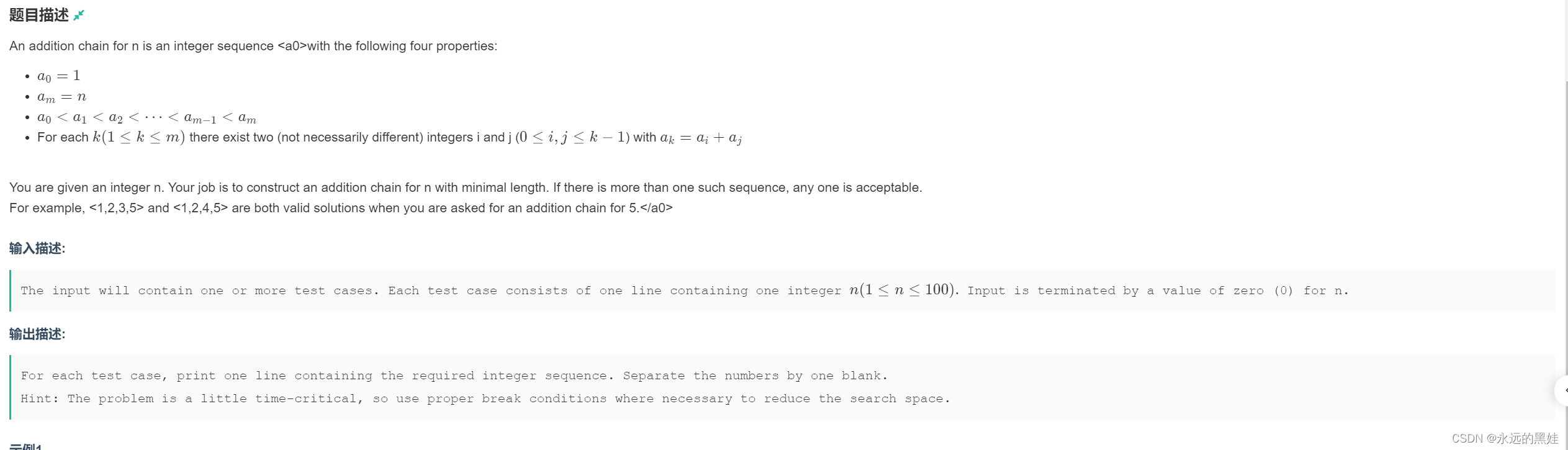
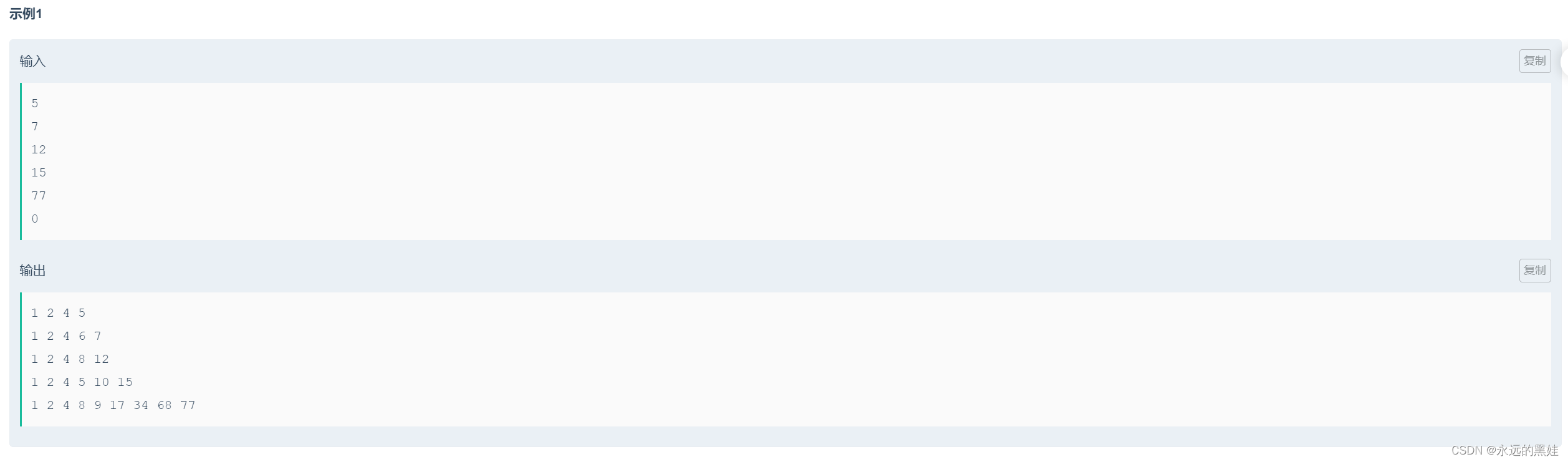
 思路:思路就是深搜填数即可。但这道题值得我们去做的原因是因为它是指定层数去遍历，当目前层数满足要求时直接输出即可。我们这里的dfs是要返回真值的，当然也可以不用返回值。

#include<bits/stdc++.h>
using namespace std;
int N;
int ans[105];
bool dfs(int dep,int deep)
{if(dep==deep)//当目前深度等于要遍历的深度时，看看填的最后一个数是否是我们输入的N即可。{return ans[dep-1]==N;}int vis[105]={0};//遍历数组for(int i=dep-1;i>=0;i--)//我们从当前遍历深度减一的位置开始填数{for(int i1=i;i1>=0;i1--){int s=ans[i]+ans[i1];if(vis[s]||s>N||s<ans[dep-1])continue;//如果数填过了或者是太大了,或是小于上次填过的数则直接跳过即可。ans[dep]=s;vis[s]=1;//赋值if(dfs(dep+1,deep))return true;//遍历下一层，这里返回真值很关键，意思是每一层的都得返回true。}}return false;
}
int main()
{while(cin>>N,N!=0){ans[0]=1;for(int i=1;i<=N;i++){if(dfs(1,i)){for(int i1=0;i1<i;i1++){cout<<" "<<ans[i1];}cout<<endl;break;}}}
}

E.weight

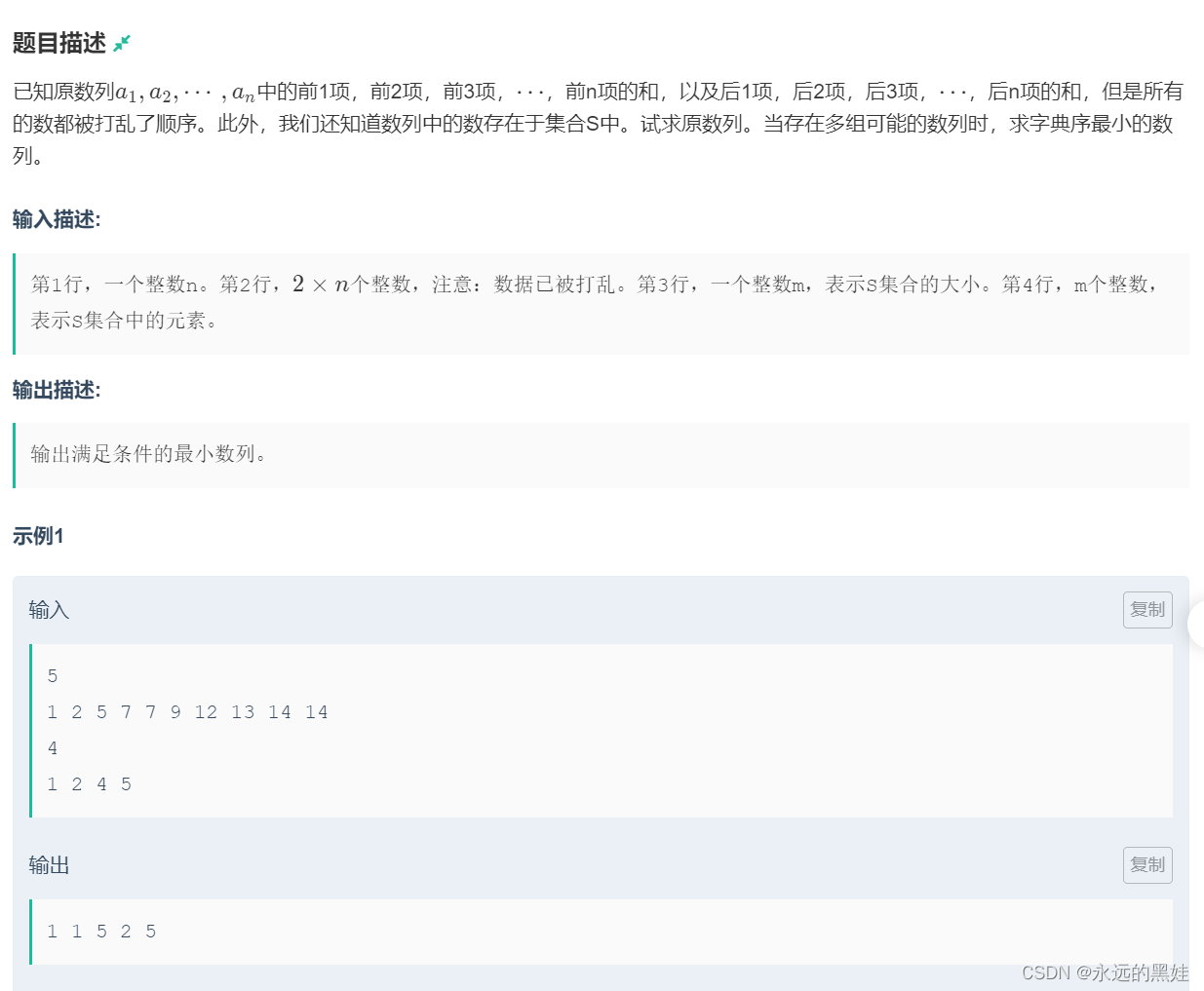
 思路：这道题我们也是要填数，但填的方法不一样，我们因为要输出最小序列所以我们要从最左填数，然后在从从右边填数即可。我们在遍历过程中我们要储存左边界值和，和右边界值和。当目前遍历到数组的值减去左边界和右边界的值的数是在数组中就填进去。之后在进行遍历，左边界值更新，和有边界值更新。

#include<bits/stdc++.h>
using namespace std;
int num[10010];
int ans[10010];
int maps[10010];
int n,m;
int sum;
void dfs(int l,int r,int sl,int sr,int index)//左右边界指针，和左右边界权值和
{if(l==r)//如果填满了直接输出程序结束，其实我们这里小用了一下贪心，直接输出的就是最小数列{int g=sum-sl-sr;//最后一个数等于总和减去左右边界的权值和if(g>=1&&g<=500&&maps[g]==1){ans[l]=g;for(int i=1;i<=n;i++)cout<<ans[i]<<" ";exit(0);}return ;}int h=num[index]-sl;if(h<=500&&maps[h])//先填左{ans[l]=h;dfs(l+1,r,num[index],sr,index+1);}int j=num[index]-sr;if(j<=500&&maps[j])//再填右{ans[r]=j;dfs(l,r-1,sl,num[index],index+1);}
}
int main()
{cin>>n;for(int i=1;i<=2*n;i++)cin>>num[i];cin>>m;for(int i=1,u;i<=m;i++){cin>>u;maps[u]=1;}sort(num+1,num+1+2*n);sum=num[2*n];dfs(1,n,0,0,1);
}

F.埃及分数

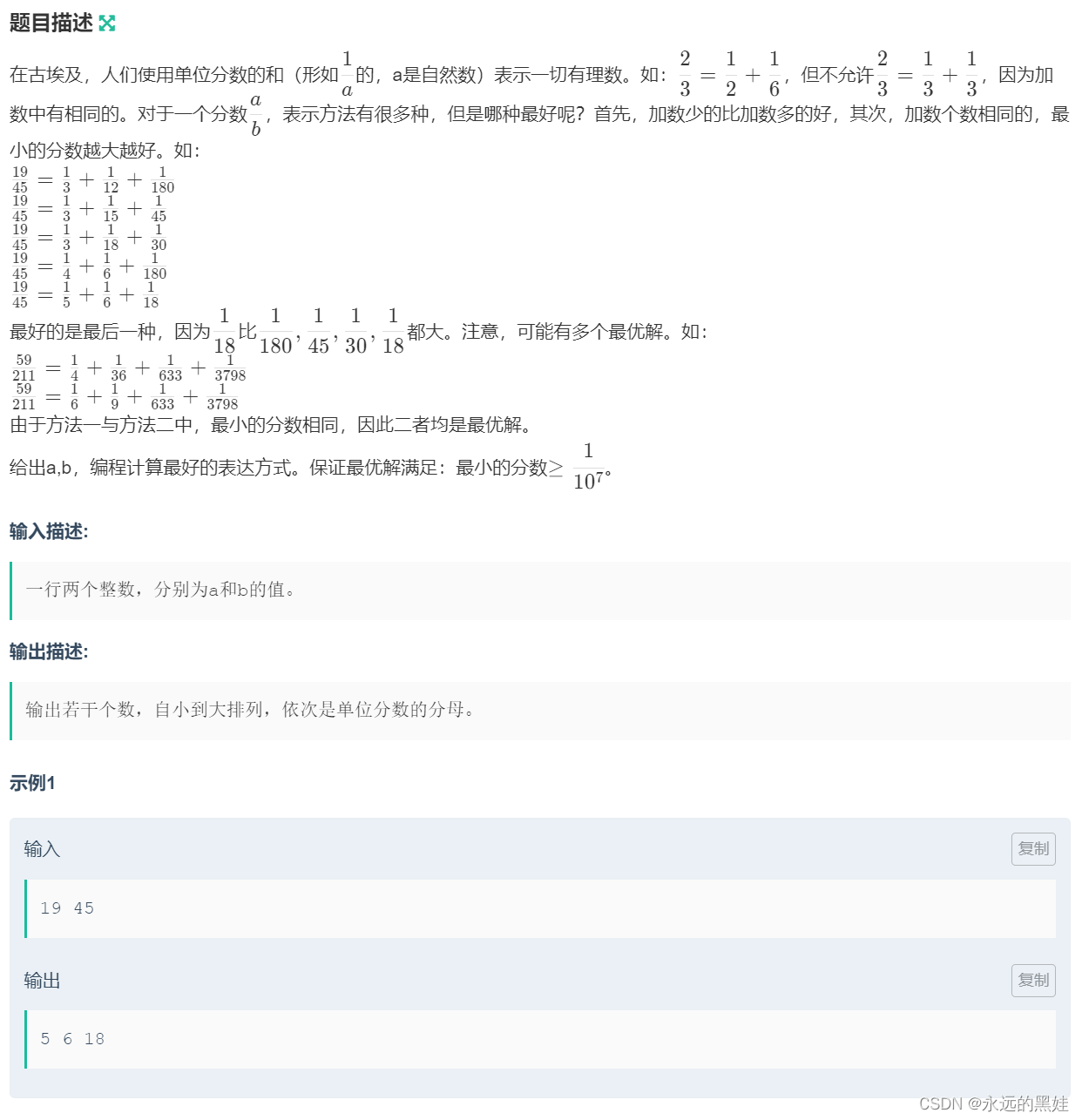
思路:因为这道题也是层数不确定所以我们也要按层数遍历，学名为迭代层数深度搜索，跟上面一道题类似，因为我们要遍历分母，枚举所有可能所有我们要回溯一下，我们每一层都减去枚举的分母，看看最后一层的时候，分子会不会减为1，减为1说明，前面的所有值都符合条件，直接输出即可。

#include<bits/stdc++.h>
#define int long long
using namespace std;
int a,b,c;
int deep;
int flag=0;
int num1[505];//储存数组
int num2[505];//答案数组
int gcd(int a,int b)
{if(b==0)return a;return gcd(b,a%b);
}
void dfs(int a,int b,int dep)
{if(dep>deep||a<0||b>1e7)//离谱值直接返回return ;if(a==1&&b>num1[dep-1])//满足条件赋值即可。{num1[dep]=b;if(!flag||num1[dep]<num2[dep])//枚举保留最大值for(int i=1;i<=dep;i++)num2[i]=num1[i];flag=1;return ;}int r=b/a*(deep-dep+1);//这个是我们遍历的最大分母（这里要用一个数学公式推一下，其实很简单）if(flag&&num2[deep]<=r)r=num2[deep]-1;//如果存在更小的我们遍历更小的for(int i=max(b/a,num1[dep-1]+1);i<r;i++){num1[dep]=i;//赋值分母dfs((a*i-b)/gcd(a*i-b,b*i),b*i/gcd(a*i-b,b*i),dep+1);//遍历减去分母分之1的值之后的num1[dep]=0;//回来}
}
signed main()
{cin>>a>>b;c=gcd(a,b);a/=c;b/=c;//最简一下for(deep=1;;deep++)//枚举深度{  dfs(a,b,1);//分子，分母，深度从1开始if(flag){for(int i=1;i<=deep;i++)cout<<num2[i]<<" ";break;}}
}

G.平板涂色

 

 思路:关于这道题我们要储存每一个色块的上面贴着的色块，我们dfs的时候我们要储存刷子数，还有上一个的颜色，还有遍历的块数，当遍历的块数等于总块数时，保留最小值，剪枝技巧是，当遍历的刷子数大于我们存储的答案就直接返回。因为我们是要求最大值所以我们还要回溯。

#include<bits/stdc++.h>
using namespace std;
const int maxn=20;
int ans=maxn;
struct node
{int x1,y1,x2,y2,w,s[maxn],t;bool vis;
}a[maxn];
int num;
bool check(int ne)
{for(int i=1;i<=a[ne].t;i++){if(!a[a[ne].s[i]].vis)return 0;}return 1;
}
void dfs(int m,int s,int last)
{if(ans<=m)return ;if(s==num){ans=min(ans,m);return ;}for(int i=1;i<=num;++i)if(!a[i].vis&&(check(i)||!a[i].y1))//可以涂的块a[i].vis=1, dfs(m+(last!=a[i].w), s+1, a[i].w), a[i].vis=0;//回溯保留最优值}
int main()
{cin>>num;for(int i=1;i<=num;i++){cin>>a[i].y1>>a[i].x1>>a[i].y2>>a[i].x2>>a[i].w;}for(int i=1;i<=num;i++){for(int j=1;j<=num;j++)if(i!=j&&a[i].y1==a[j].y2&&!(a[j].x2<a[i].x1||a[j].x1>a[i].x2))a[i].s[++a[i].t]=j; }dfs(0,0,0);cout<<ans;
}

I.靶形数独

 

 

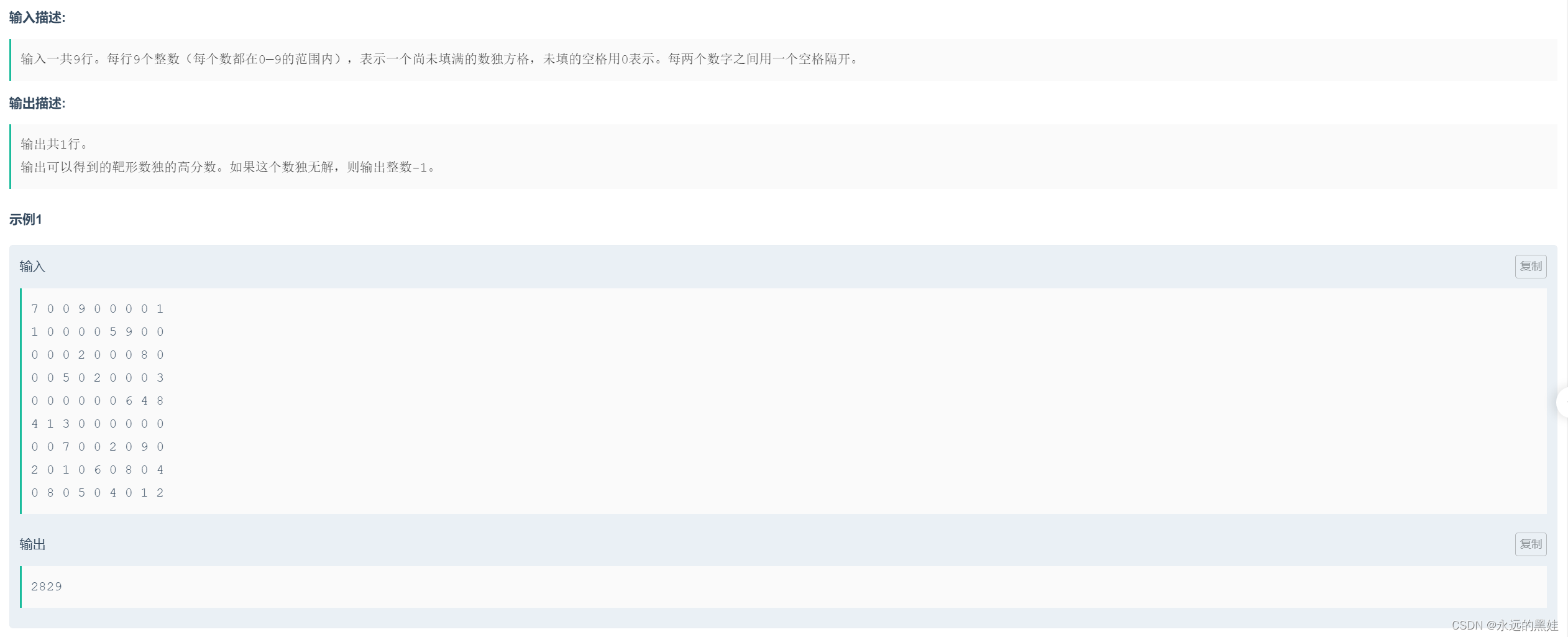
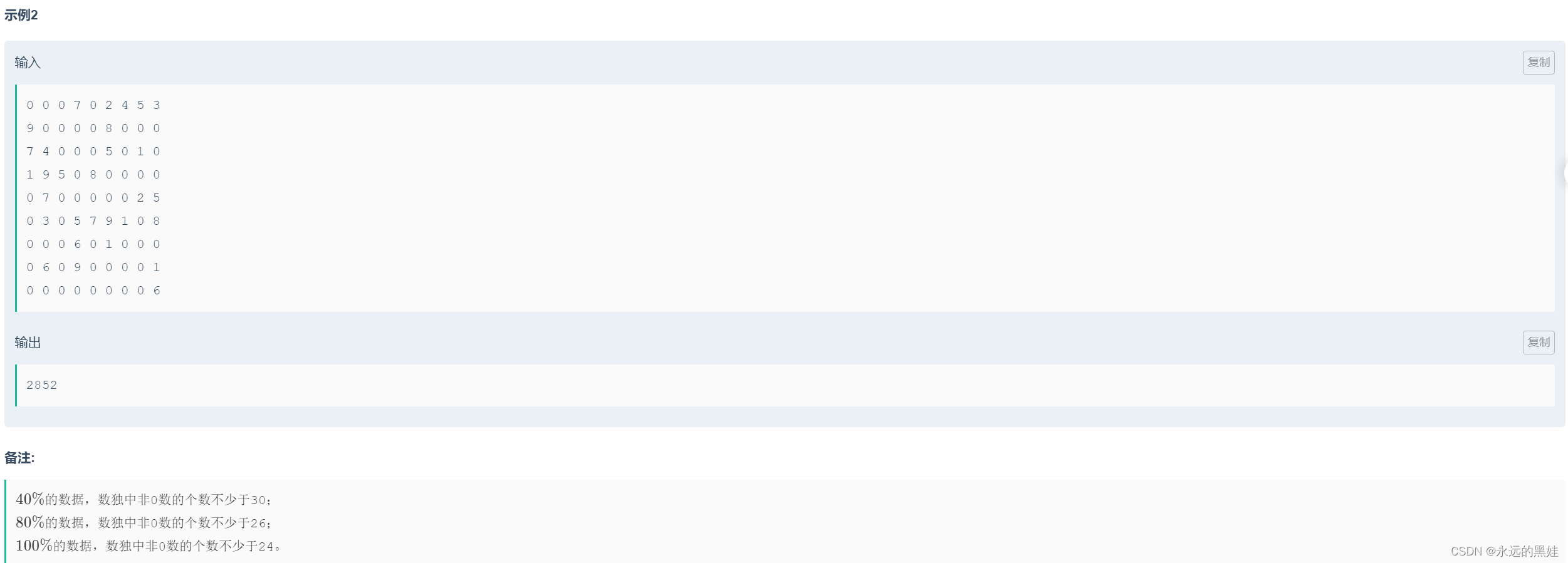
思路：这道题我们要学会打表，我们记录每一次的填数记录，因为填数过程中难免会发生填数失败，所以我们要回溯。具体如下

​
#include <bits/stdc++.h>
using namespace std;
int a[10][10],ans=0,mans=-1,t;
bool h[10][10], l[10][10], g[10][10];//看看是否填过了
int pre[9][9] = {1, 1, 1, 2, 2, 2, 3, 3, 3,1, 1, 1, 2, 2, 2, 3, 3, 3,1, 1, 1, 2, 2, 2, 3, 3, 3,4, 4, 4, 5, 5, 5, 6, 6, 6,4, 4, 4, 5, 5, 5, 6, 6, 6,4, 4, 4, 5, 5, 5, 6, 6, 6,7, 7, 7, 8, 8, 8, 9, 9, 9,7, 7, 7, 8, 8, 8, 9, 9, 9,7, 7, 7, 8, 8, 8, 9, 9, 9};//打表区域表
int s[9][9]={6,6,6,6,6,6,6,6,6,6,7,7,7,7,7,7,7,6,6,7,8,8,8,8,8,7,6,6,7,8,9,9,9,8,7,6,6,7,8,9,10,9,8,7,6,6,7,8,9,9,9,8,7,6,6,7,8,8,8,8,8,7,6,6,7,7,7,7,7,7,7,6,6,6,6,6,6,6,6,6,6
};//分数表
void dfs(int k) {t++;//这个值是特判超时值if(t>1e7+2e6)return ;//太多了直接返回if (k <0) {ans=0;for (int i = 0; i < 9; i++) {for (int j = 0; j < 9; j++) {ans+=a[i][j]*s[i][j];}}mans=max(mans,ans);//我们保留最大分数return;}int x = k / 9;//当前行int y = k % 9;//当前列if (a[x][y] > 0) dfs(k - 1);//当前位置不填数else {for (int i = 1; i <= 9; i++) {//填1~9，依次填依次遍历if (!h[x][i] && !l[y][i] && !g[pre[x][y]][i]) {h[x][i] = 1;l[y][i] = 1;g[pre[x][y]][i] = 1;a[x][y] = i;dfs(k - 1);a[x][y] = 0;h[x][i] = 0;l[y][i] = 0;g[pre[x][y]][i] = 0;}}}
}
int main() {for (int i = 0; i < 9; i++) {for (int j = 0; j < 9; j++) {cin >> a[i][j];int x = a[i][j];h[i][x] = 1;//行数l[j][x] = 1;//列数g[pre[i][j]][x] = 1;//区域数}}dfs(80);cout<<mans;return 0;
}​