做网站打电话话术江西省水文监测中心

“”"
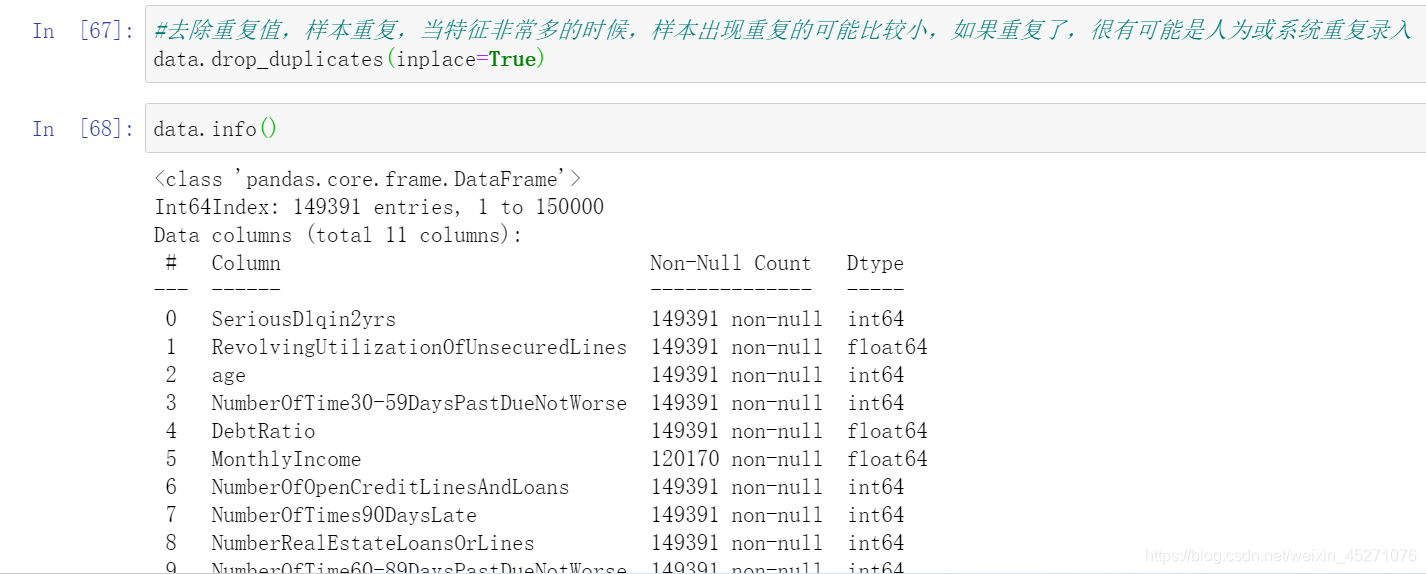
使用随机森林填补一个特征的缺失值的函数
参数：
X：要填补的特征矩阵
y：完整的，没有缺失值的标签
to_fill：字符串，要填补的那一列的名称
“”"

def fill_missing_rf(X,y,to_fill):#构建我们的新特征矩阵和新标签df = X.copy()fill = df.loc[:,to_fill]df = pd.concat([df.loc[:,df.columns != to_fill],pd.DataFrame(y)],axis=1)#找出我们的训练集和测试集Ytrain = fill[fill.notnull()]Ytest = fill[fill.isnull()]Xtrain = df.iloc[Ytrain.index,:]Xtest = df.iloc[Ytest.index,:]#用随机森林回归来填补缺失值from sklearn.ensemble import RandomForestRegressor as rfrrfr = rfr(n_estimators=100)rfr = rfr.fit(Xtrain, Ytrain)Ypredict = rfr.predict(Xtest)return Ypredict

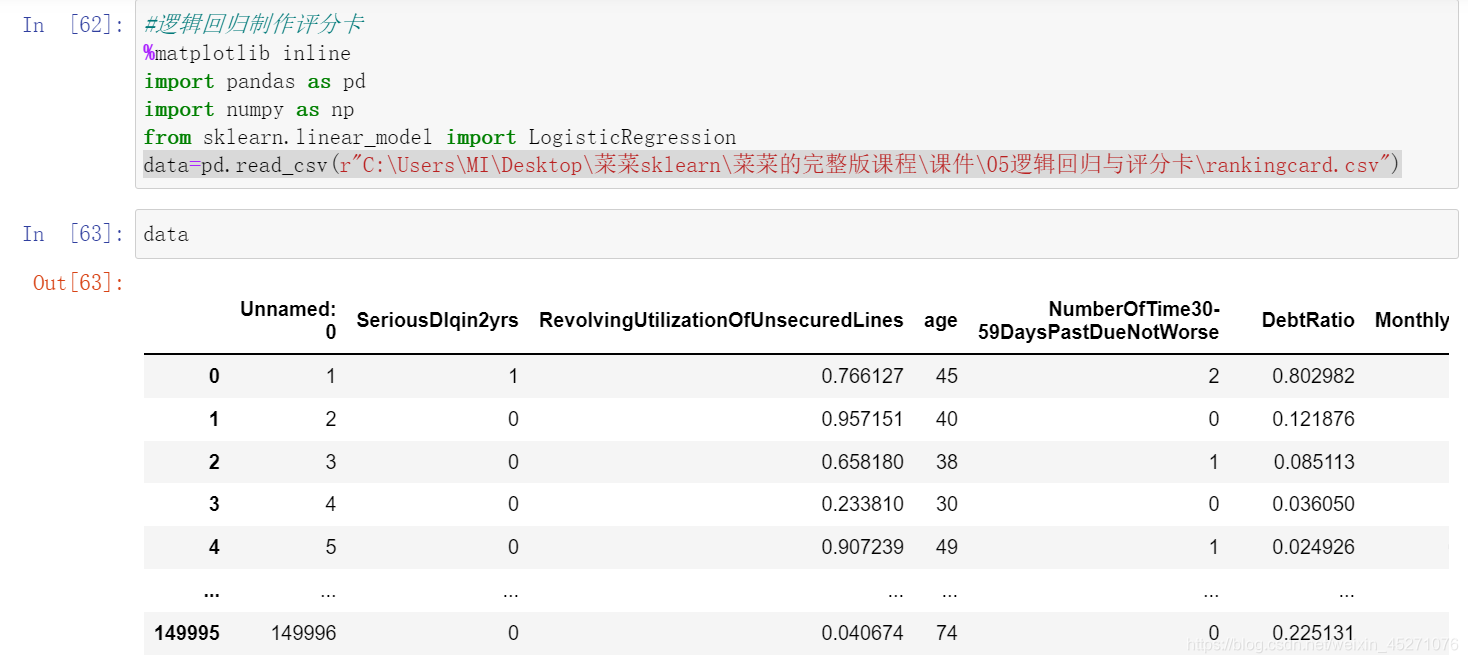
X = data.iloc[:,1:]
y = data["SeriousDlqin2yrs"]
X.shape
#=====【TIME WARNING：1 min】=====#
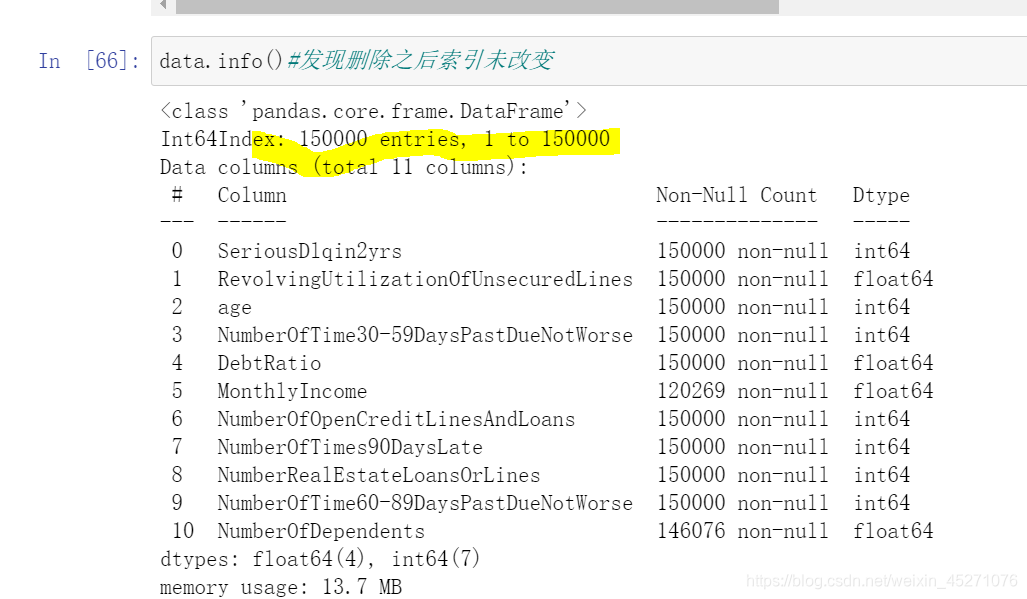
y_pred = fill_missing_rf(X,y,"MonthlyIncome")
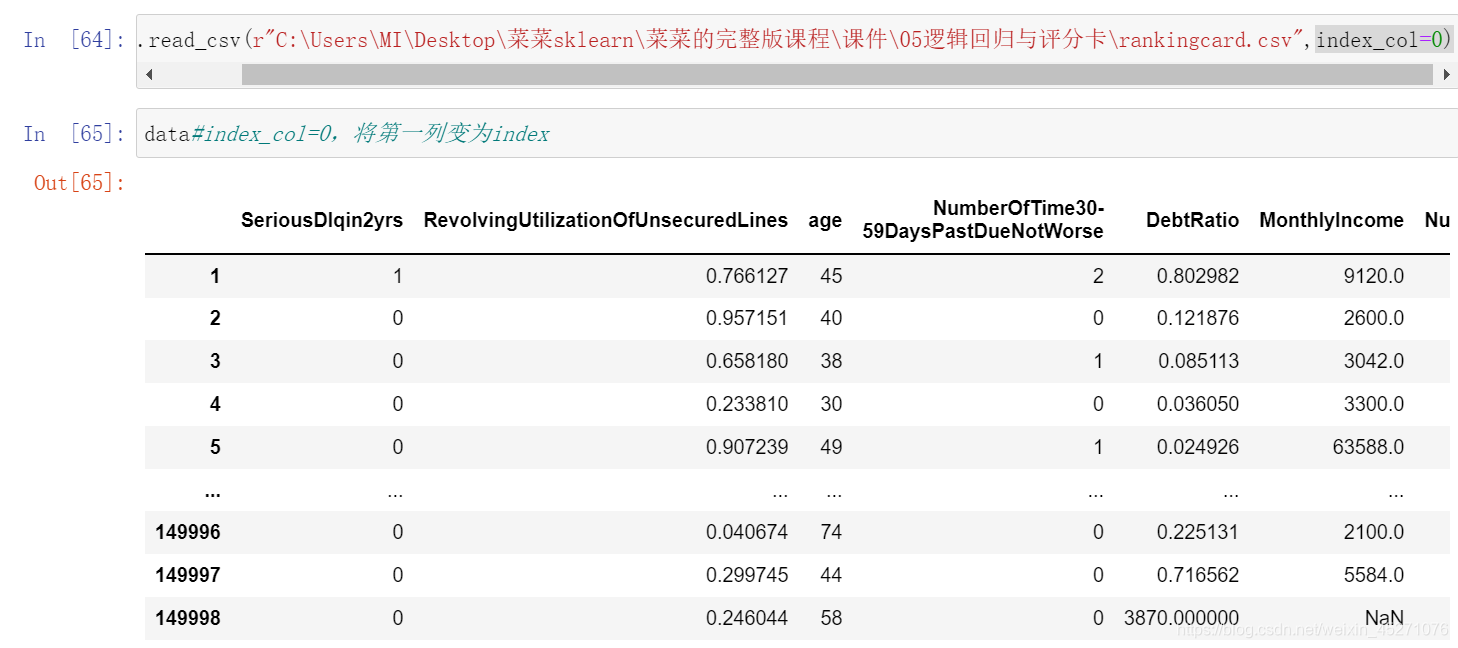
#确认我们的结果合理之后，我们就可以将数据覆盖了
data.loc[data.loc[:,"MonthlyIncome"].isnull(),"MonthlyIncome"] = y_pred

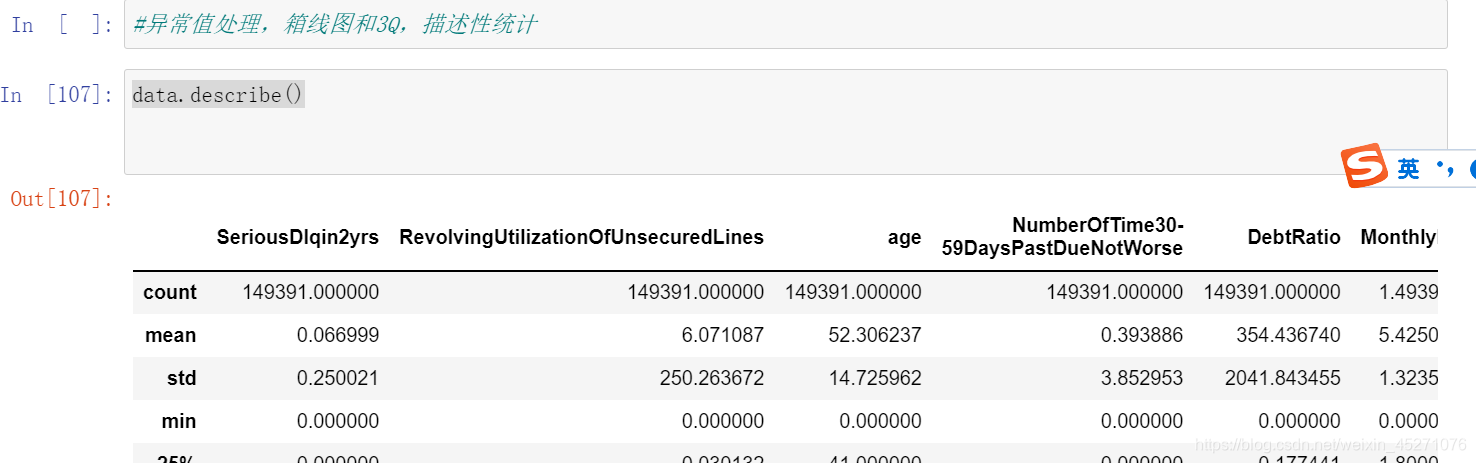
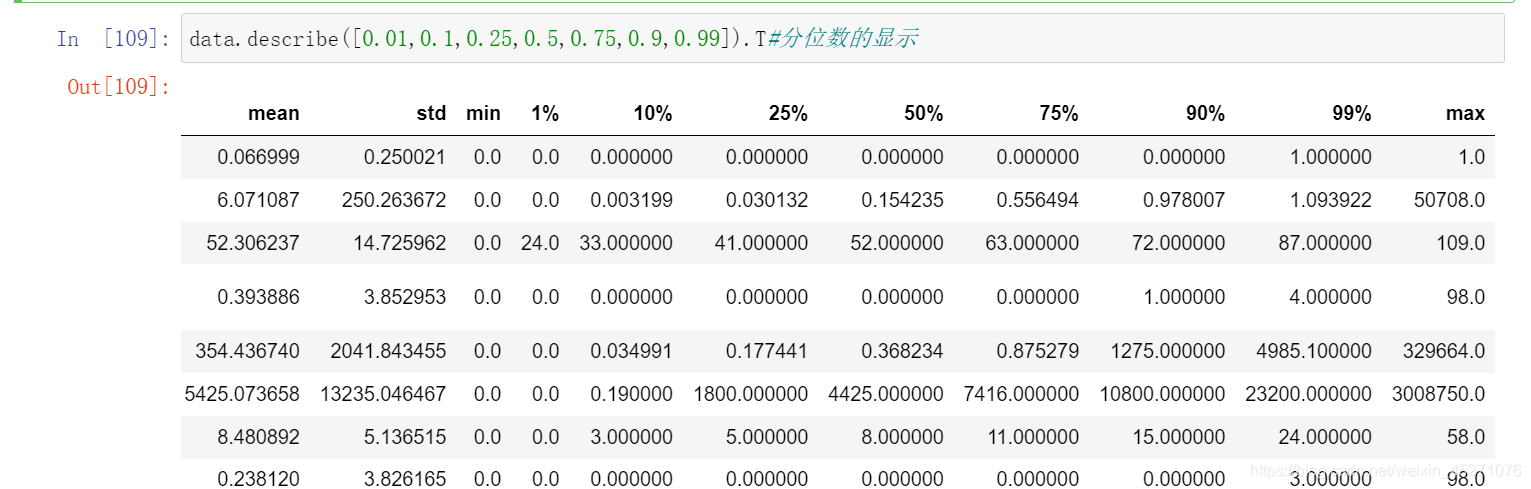
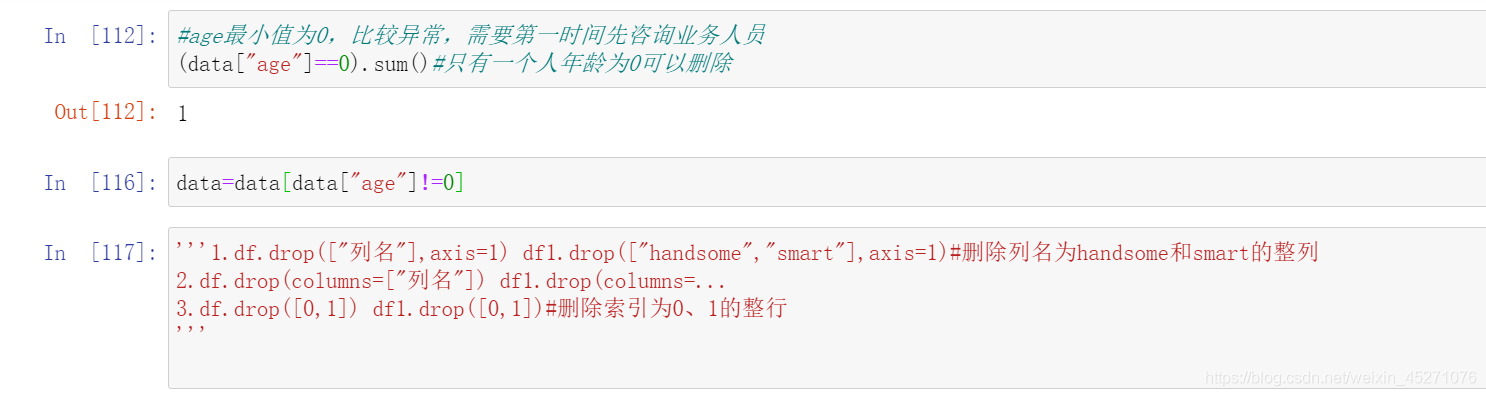
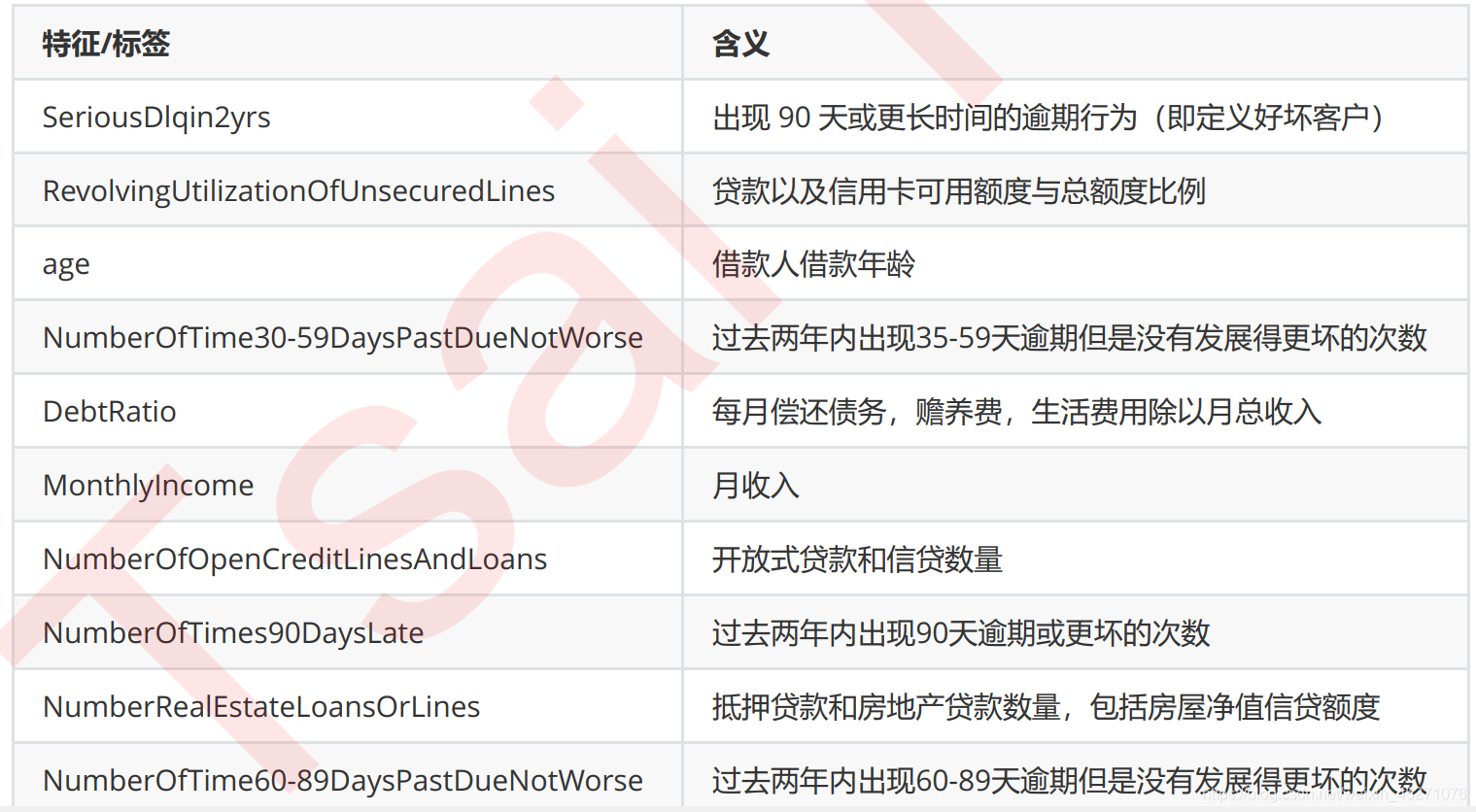
‘’‘另外，有三个指标看起来很奇怪：
“NumberOfTime30-59DaysPastDueNotWorse”
“NumberOfTime60-89DaysPastDueNotWorse”
“NumberOfTimes90DaysLate”
这三个指标分别是“过去两年内出现35-59天逾期但是没有发展的更坏的次数”，“过去两年内出现60-89天逾期但是没
有发展的更坏的次数”,“过去两年内出现90天逾期的次数”。这三个指标，在99%的分布的时候依然是2，最大值却是
98，看起来非常奇怪。一个人在过去两年内逾期35~59天98次，一年6个60天，两年内逾期98次这是怎么算出来的？
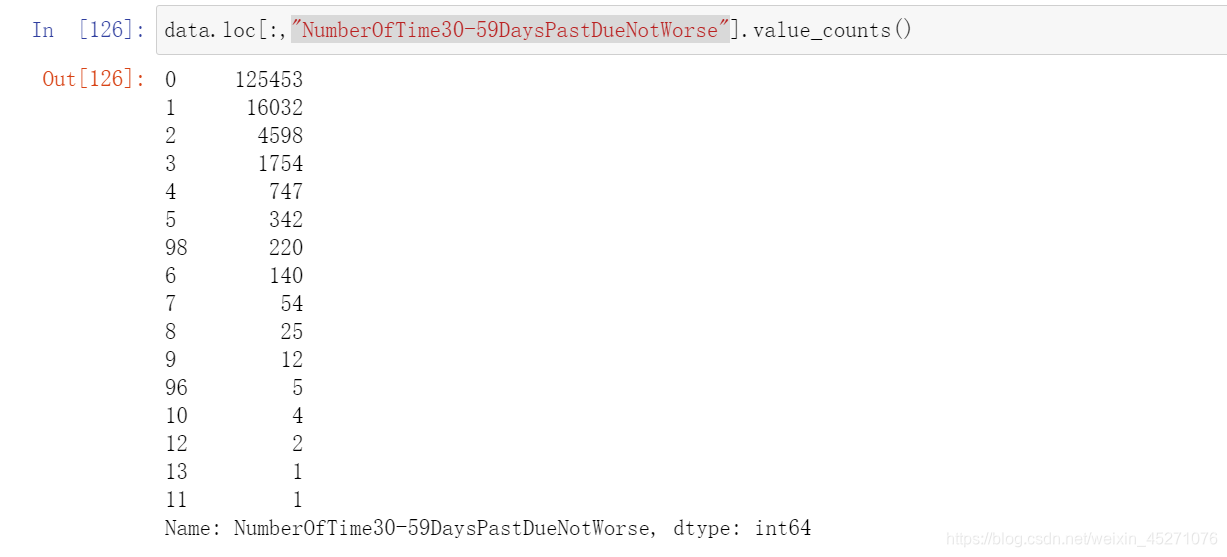
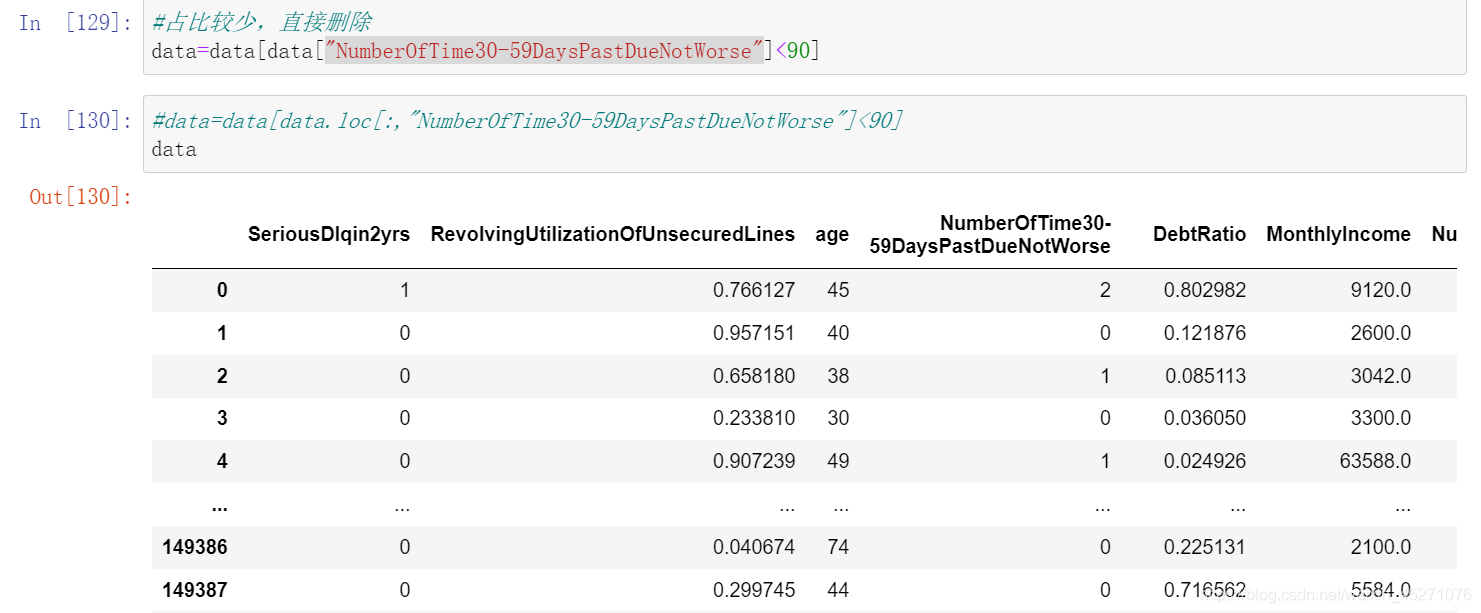
我们可以去咨询业务人员，请教他们这个逾期次数是如何计算的。如果这个指标是正常的，那这些两年内逾期了98次的
客户，应该都是坏客户。在我们无法询问他们情况下，我们查看一下有多少个样本存在这种异常：’’’

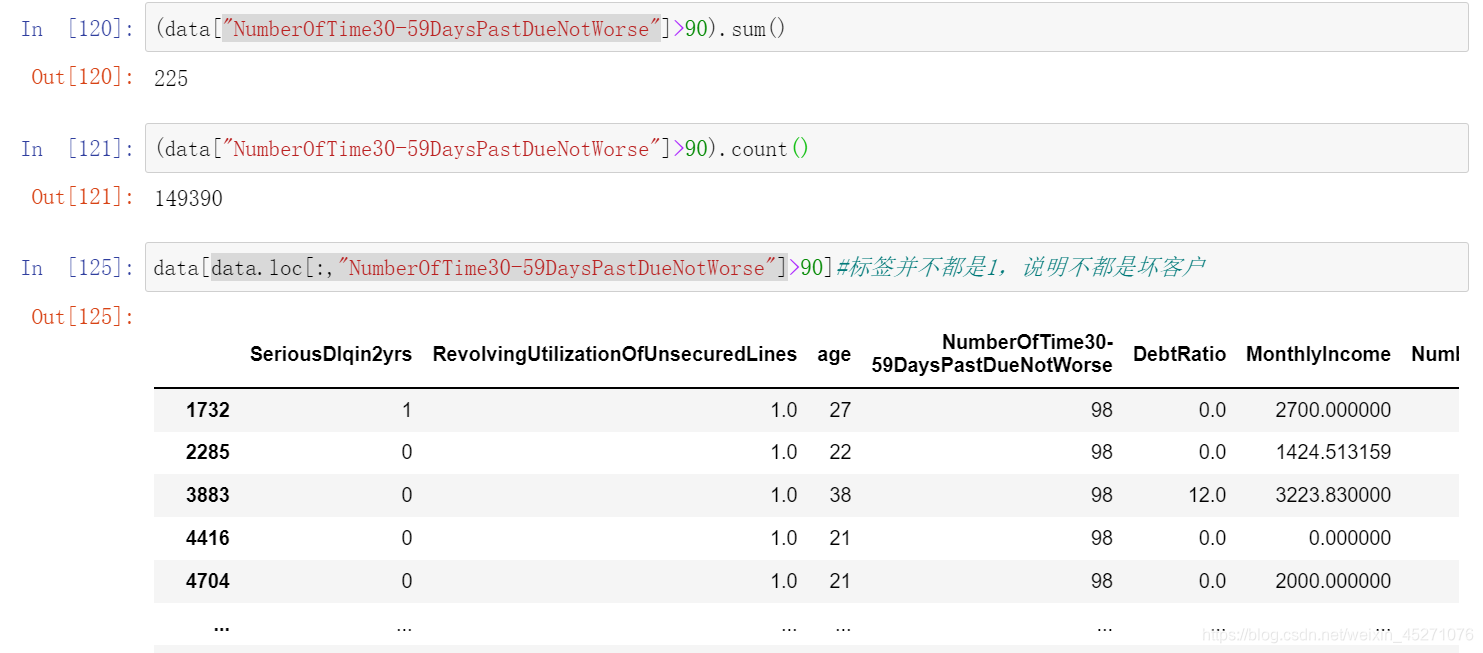
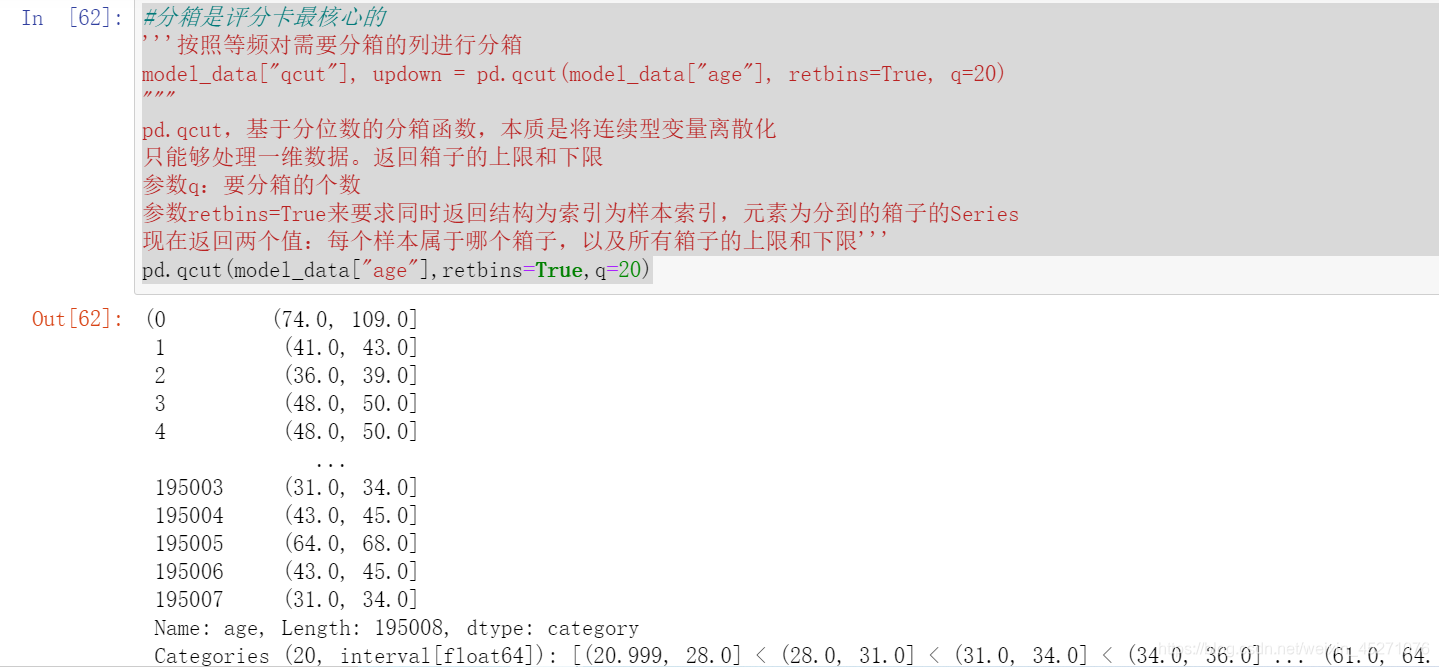
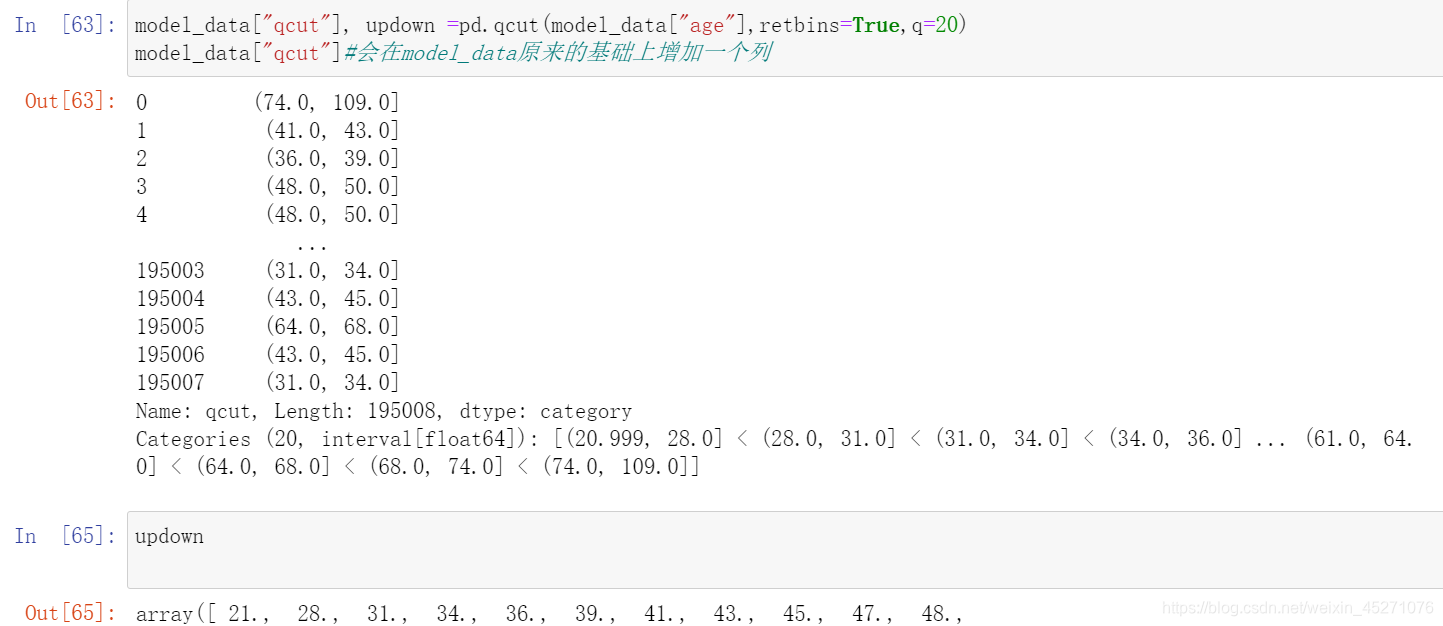
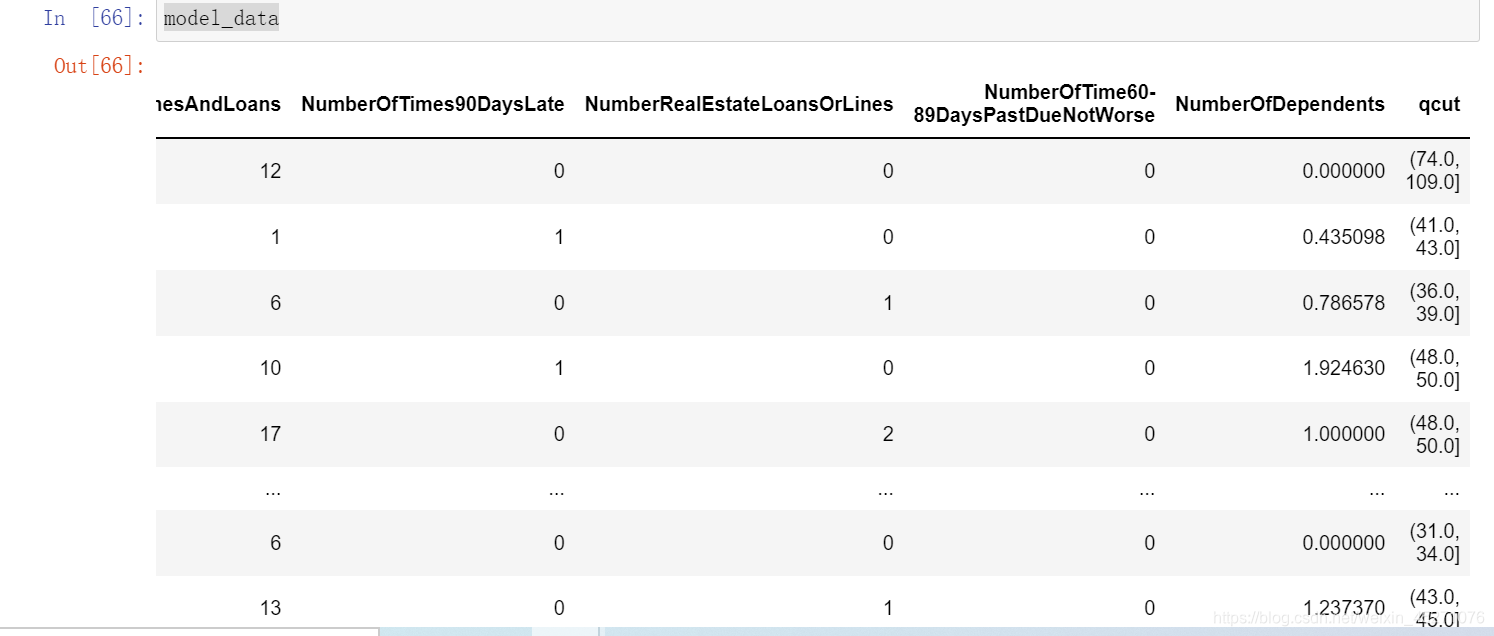
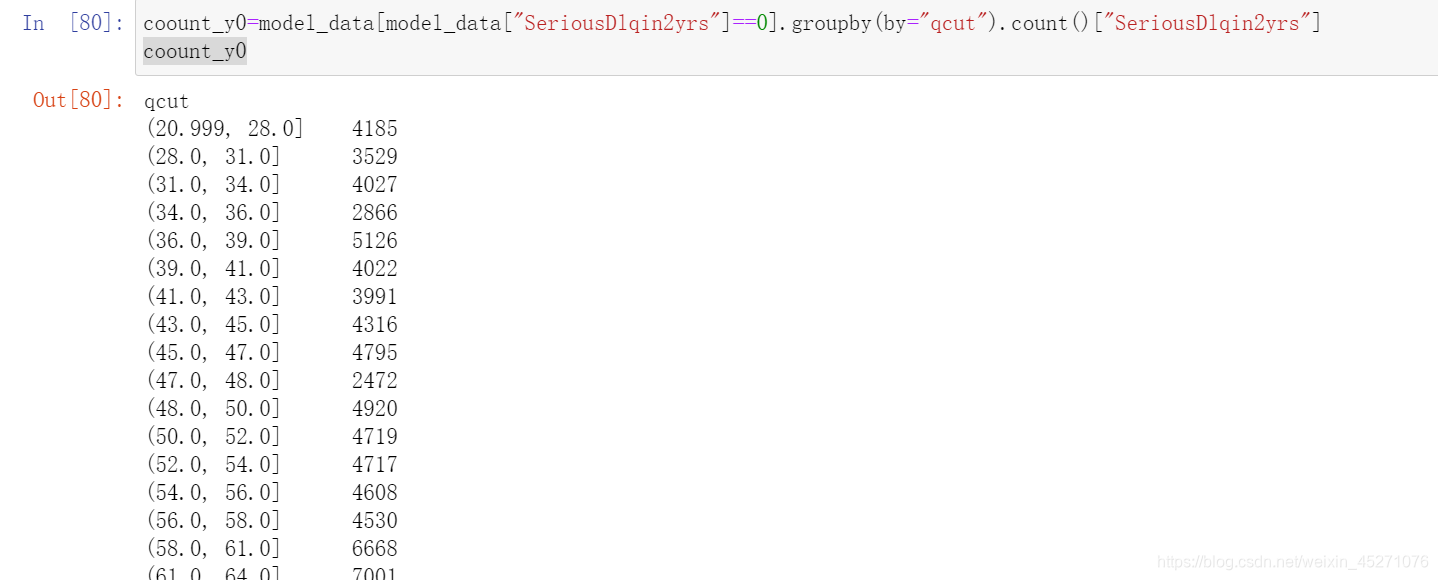
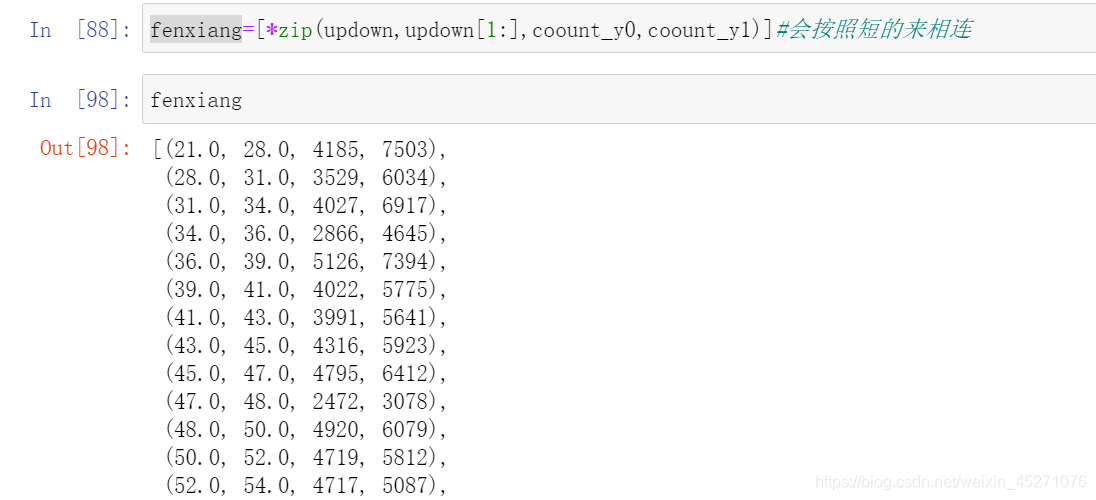
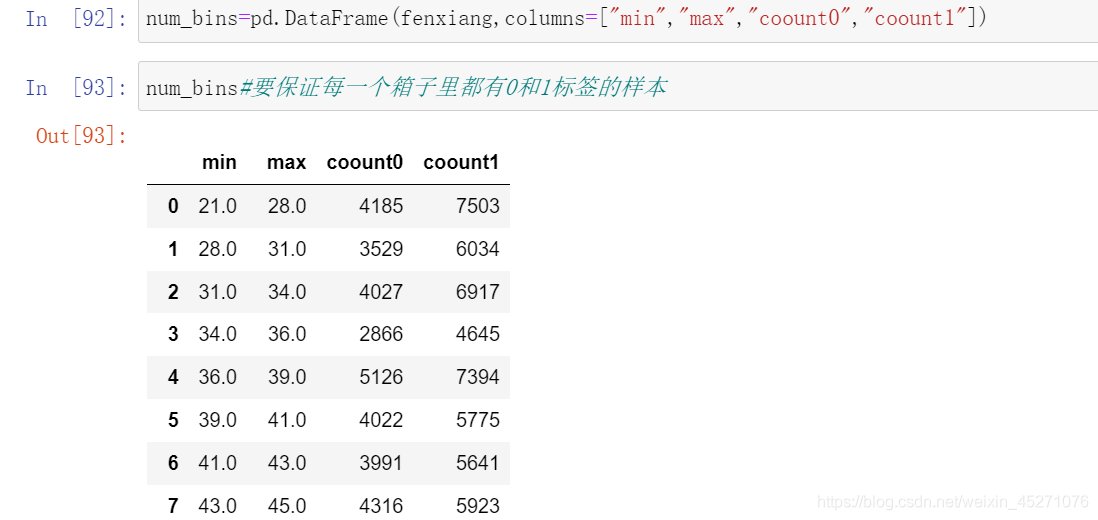
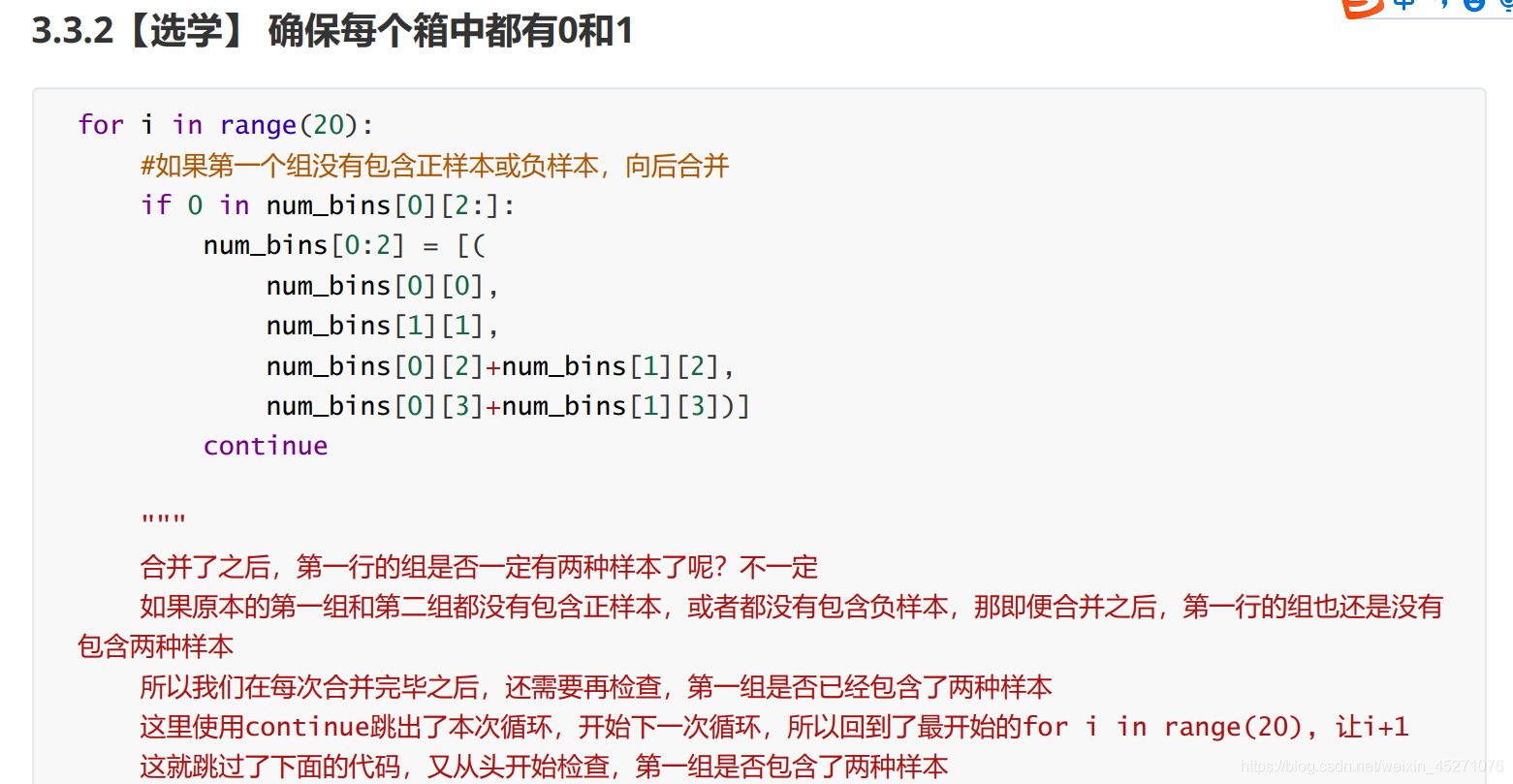
#定义woe iv函数
#计算WOE和BAD RATE
#BAD RATE与bad%不是一个东西
#BAD RATE是一个箱中，坏的样本所占的比例 (bad/total)
#而bad%是一个箱中的坏样本占整个特征中的坏样本的比例
def get_woe(num_bins):#columns=["min","max","count_0","count_1"]df=num_bins.copy()df["total"]=df["coount0"]+df["coount1"]df["percentage"]=df.total/df.total.sum()df["bad_rate"]=df.coount1/df.totaldf["good%"]=df.coount0/df.coount0.sum()df["bad%"]=df.coount1/df.coount1.sum()df["woe"]=np.log(df["good%"]/df["bad%"])return df

def get_iv(df):rate=df["good%"]-df["bad%"]iv=np.sum(rate*df.woe)return iv

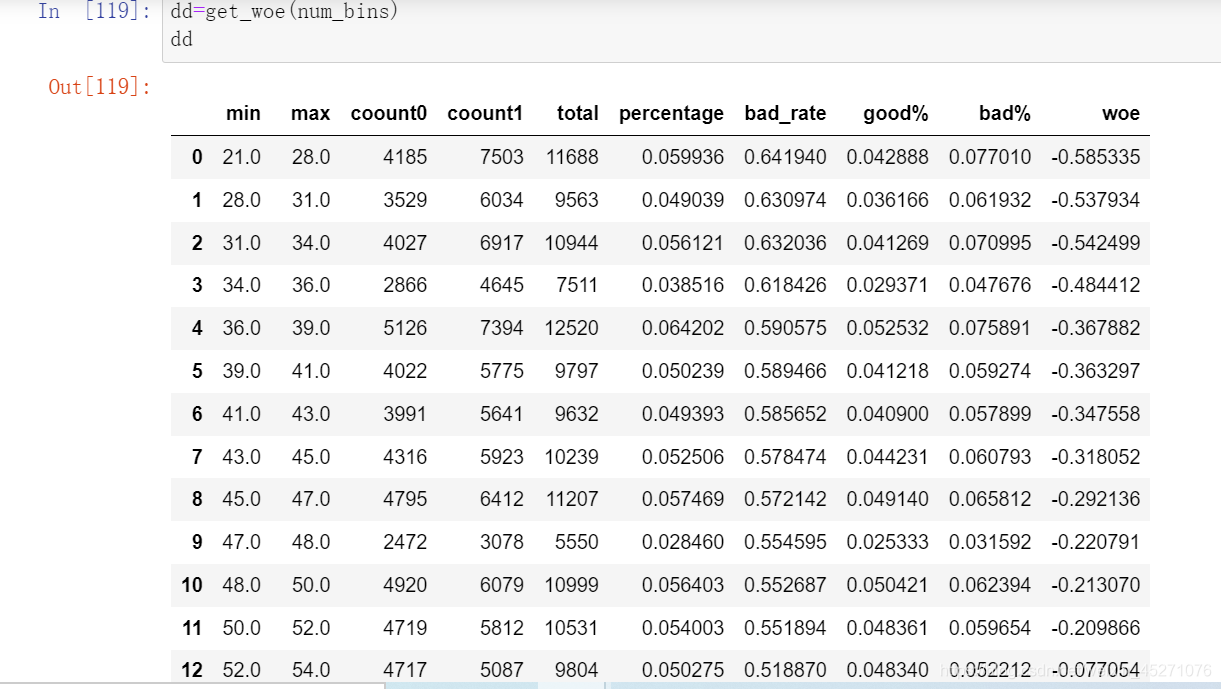
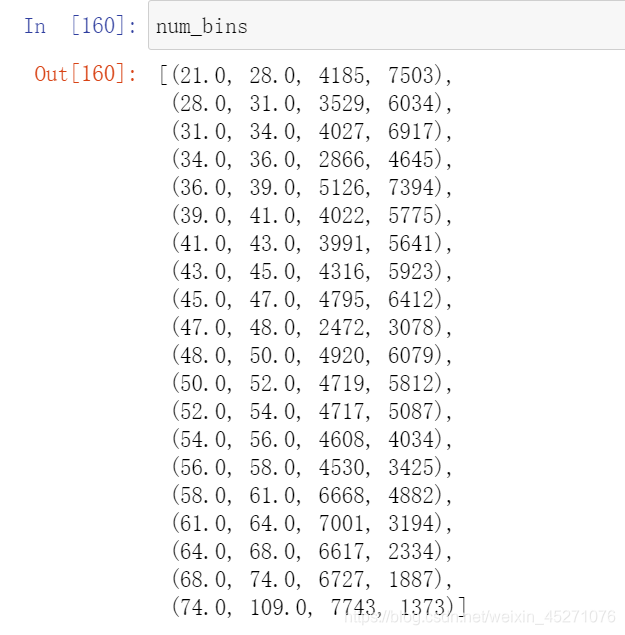
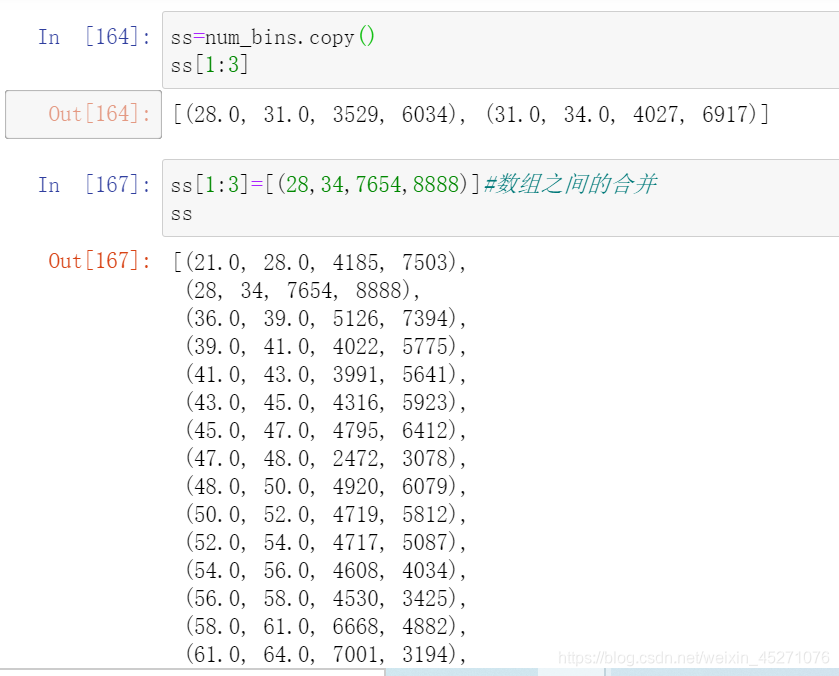
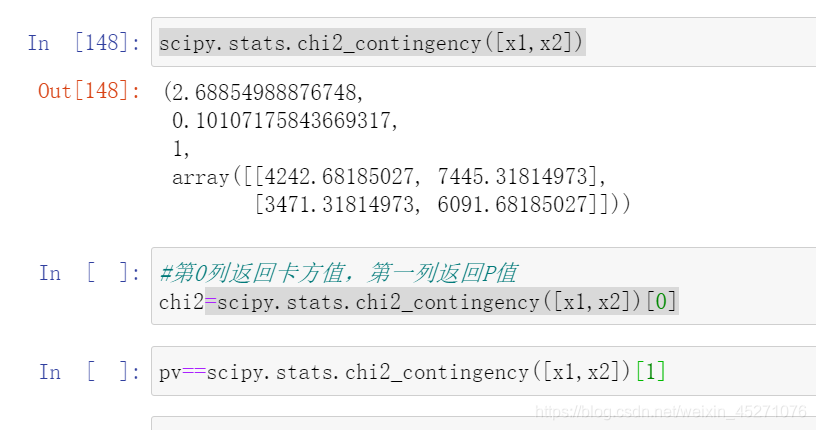
#卡方检验，合并箱体
num_bins1=num_bins.copy()
import matplotlib.pyplot as plt
import scipy
IV=[]
axis=[]
while len(num_bins1)>2:pvs=[]#获取箱子两两之间的卡方检验置信度或卡方值for i in range(len(num_bins1)-1):x1=num_bins1[i][2:]x2=num_bins1[i+1][2:]pv=scipy.stats.chi2_contingency([x1,x2])[1]pvs.append(pv)#第一轮循环完了之后，查找P值最大的，并把那两个X1 X2合并为1列i=pvs.index(max(pvs))num_bins1[i:i+2]=[(num_bins1[i][0],num_bins1[i+1][1],num_bins1[i][2]+num_bins1[i+1][2],num_bins1[i][3]+num_bins1[i+1][3])]bis_df=get_woe(num_bins1)axis.append(len(num_bins1))IV.append(get_iv(bis_df))

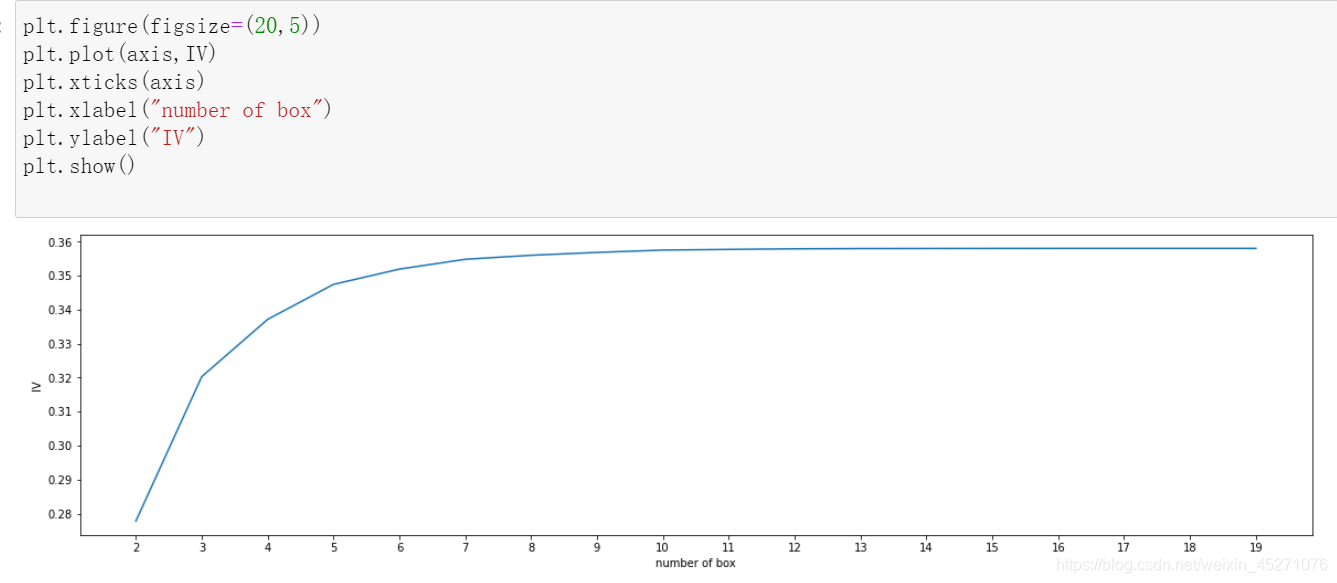
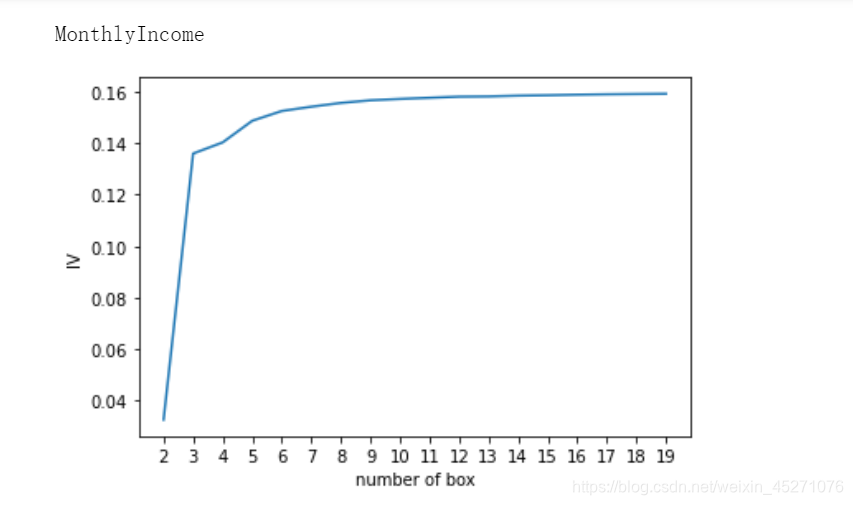
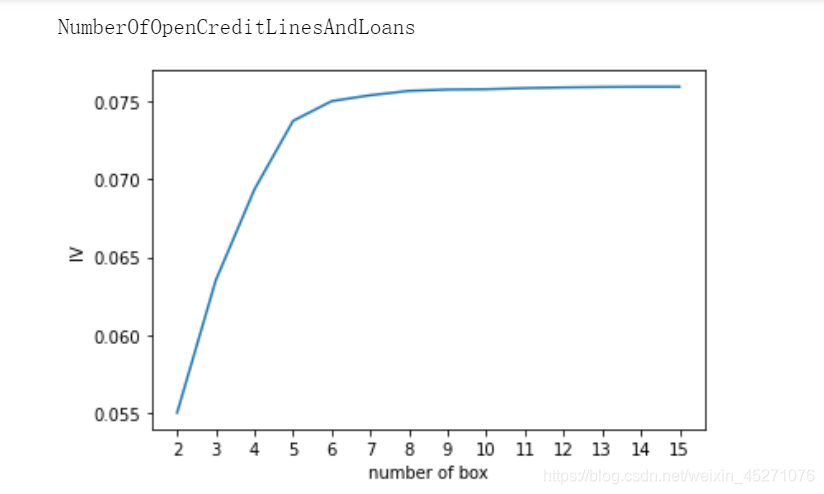
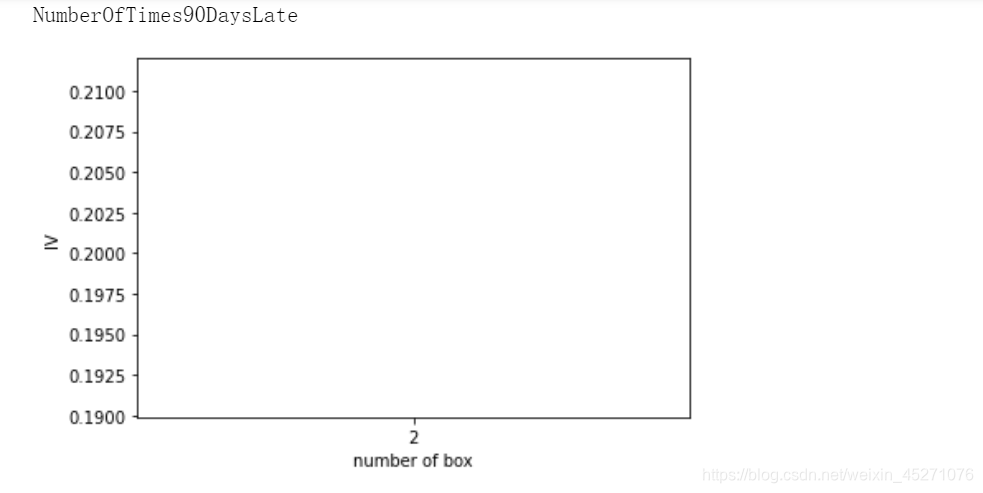
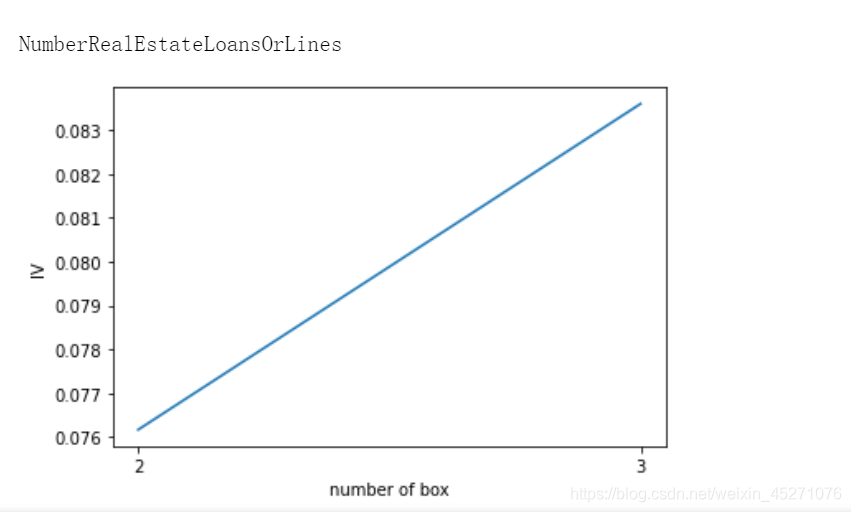
def graphforbestbin(DF, X, Y, n=5,q=20,graph=True):"""自动最优分箱函数，基于卡方检验的分箱参数：DF: 需要输入的数据X: 需要分箱的列名Y: 分箱数据对应的标签 Y 列名n: 保留分箱个数q: 初始分箱的个数graph: 是否要画出IV图像区间为前开后闭 (]"""DF = DF[[X,Y]].copy()DF["qcut"],bins = pd.qcut(DF[X], retbins=True, q=q,duplicates="drop")coount_y0 = DF.loc[DF[Y]==0].groupby(by="qcut").count()[Y]coount_y1 = DF.loc[DF[Y]==1].groupby(by="qcut").count()[Y]num_bins = [*zip(bins,bins[1:],coount_y0,coount_y1)]for i in range(q):if 0 in num_bins[0][2:]:num_bins[0:2] = [(num_bins[0][0],num_bins[1][1],num_bins[0][2]+num_bins[1][2],num_bins[0][3]+num_bins[1][3])]continuefor i in range(len(num_bins)):if 0 in num_bins[i][2:]:num_bins[i-1:i+1] = [(num_bins[i-1][0],num_bins[i][1],num_bins[i-1][2]+num_bins[i][2],num_bins[i-1][3]+num_bins[i][3])]breakelse:breakdef get_woe(num_bins):columns = ["min","max","count_0","count_1"]df = pd.DataFrame(num_bins,columns=columns)df["total"] = df.count_0 + df.count_1df["percentage"] = df.total / df.total.sum()df["bad_rate"] = df.count_1 / df.totaldf["good%"] = df.count_0/df.count_0.sum()df["bad%"] = df.count_1/df.count_1.sum()df["woe"] = np.log(df["good%"] / df["bad%"])return dfdef get_iv(df):rate = df["good%"] - df["bad%"]iv = np.sum(rate * df.woe)return ivIV = []axisx = []while len(num_bins) > n:pvs = []for i in range(len(num_bins)-1):x1 = num_bins[i][2:]x2 = num_bins[i+1][2:]pv = scipy.stats.chi2_contingency([x1,x2])[1]pvs.append(pv)i = pvs.index(max(pvs))num_bins[i:i+2] = [(num_bins[i][0],num_bins[i+1][1],num_bins[i][2]+num_bins[i+1][2],num_bins[i][3]+num_bins[i+1][3])]bins_df1 = pd.DataFrame(get_woe(num_bins))axisx.append(len(num_bins))IV.append(get_iv(bins_df1))if graph:plt.figure()plt.plot(axisx,IV)plt.xticks(axisx)plt.xlabel("number of box")plt.ylabel("IV")plt.show()return bins_df1

for i in model_data.columns[1:-1]:print(i)graphforbestbin(model_data,i,"SeriousDlqin2yrs",n=2,q=20)

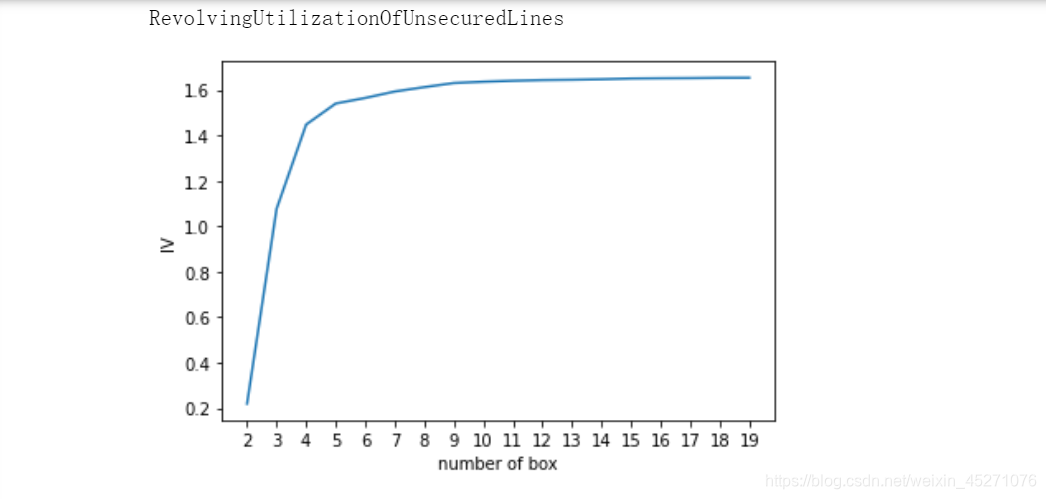
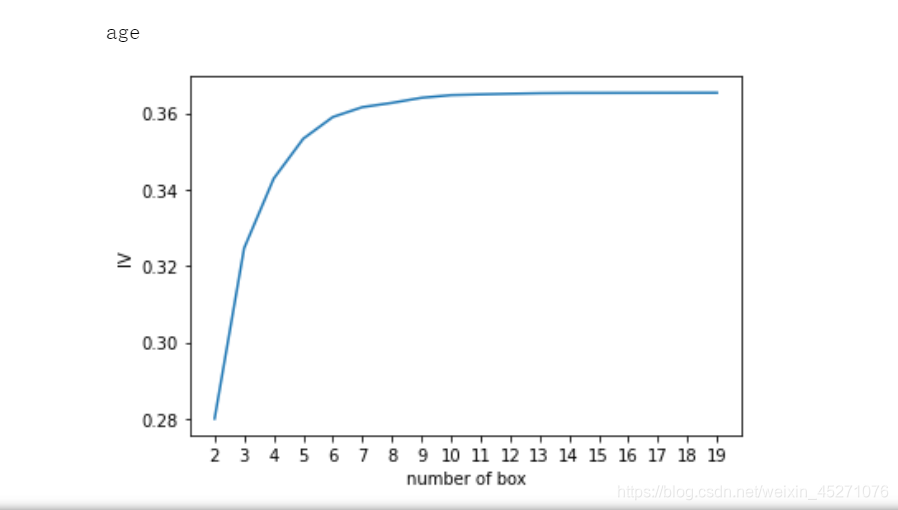
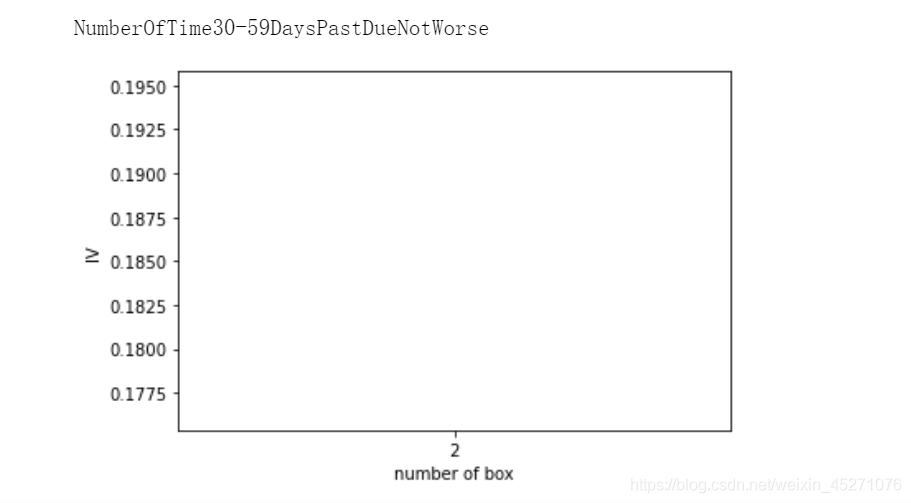
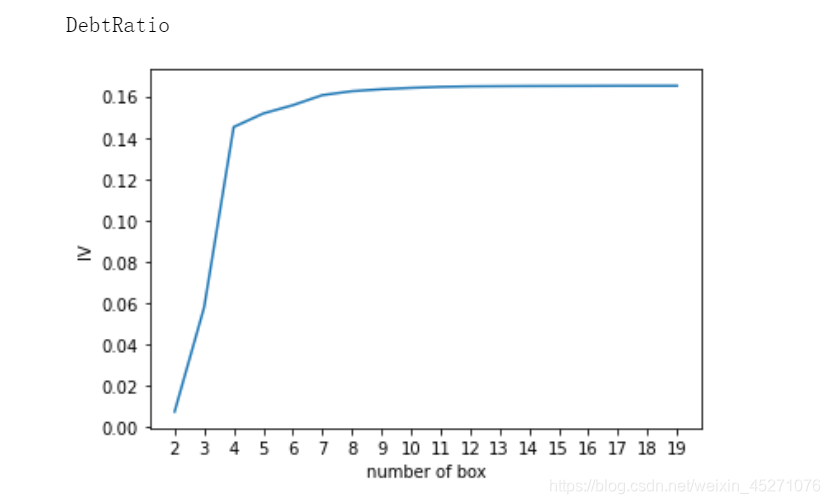
auto_col_bins = {"RevolvingUtilizationOfUnsecuredLines":6,
"age":5,
"DebtRatio":4,
"MonthlyIncome":3,
"NumberOfOpenCreditLinesAndLoans":5}
#不能使用自动分箱的变量
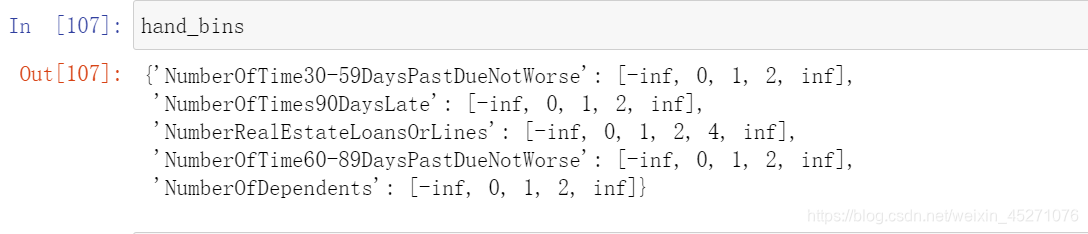
hand_bins = {"NumberOfTime30-59DaysPastDueNotWorse":[0,1,2,13]
,"NumberOfTimes90DaysLate":[0,1,2,17]
,"NumberRealEstateLoansOrLines":[0,1,2,4,54]
,"NumberOfTime60-89DaysPastDueNotWorse":[0,1,2,8]
,"NumberOfDependents":[0,1,2,3]}
#保证区间覆盖使用 np.inf替换最大值，用-np.inf替换最小值
hand_bins = {k:[-np.inf,*v[:-1],np.inf] for k,v in hand_bins.items()}

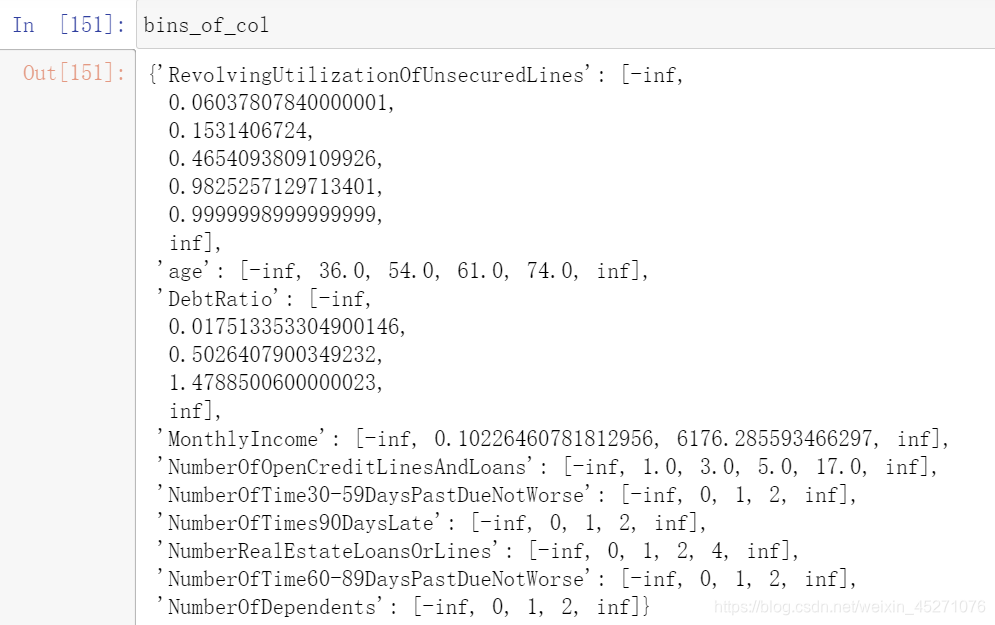
bins_of_col={}
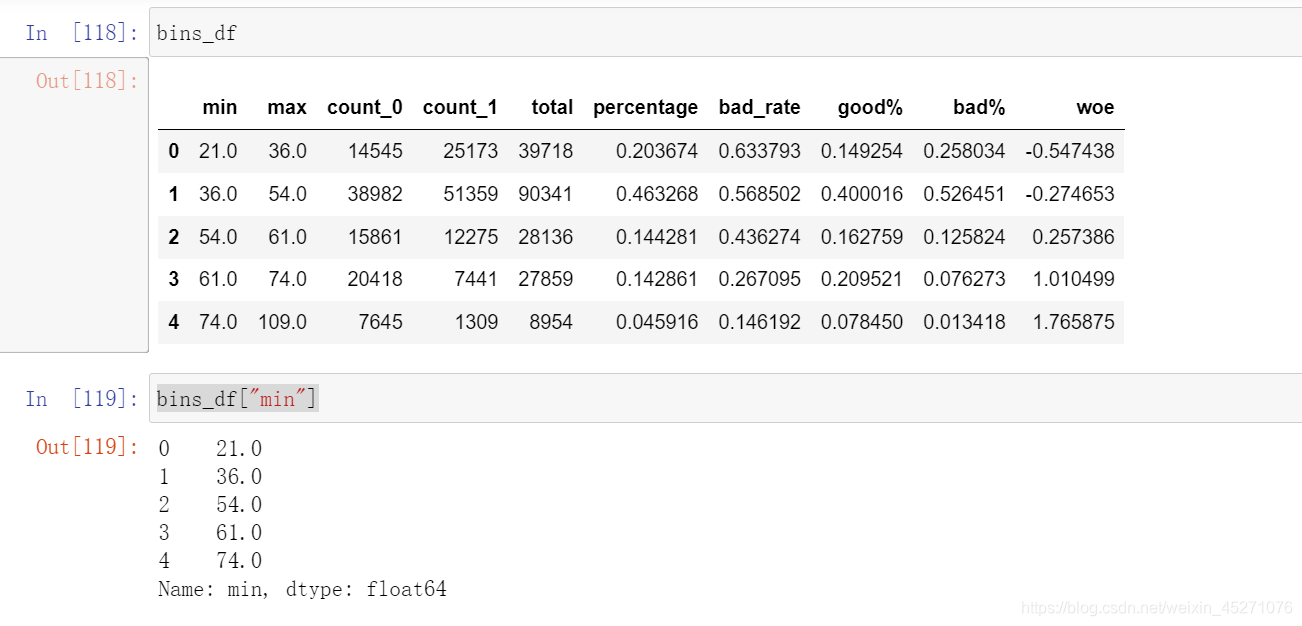
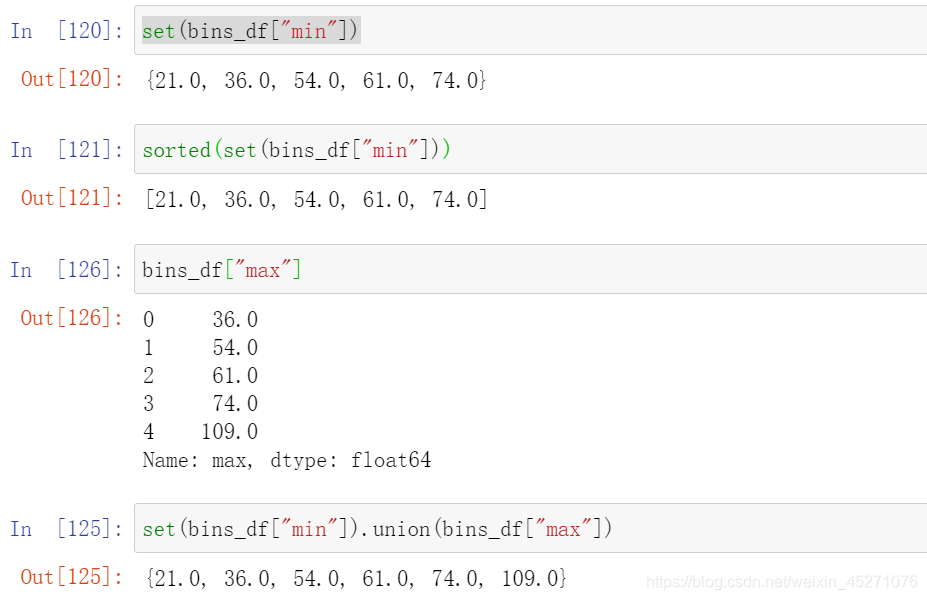
for col in auto_col_bins:bins_df=graphforbestbin(model_data,col,"SeriousDlqin2yrs",n=auto_col_bins[col],q=20,graph=False)bins_list = sorted(set(bins_df["min"]).union(bins_df["max"]))
#保证区间覆盖使用 np.inf 替换最大值 -np.inf 替换最小值bins_list[0],bins_list[-1] = -np.inf,np.infbins_of_col[col] = bins_list

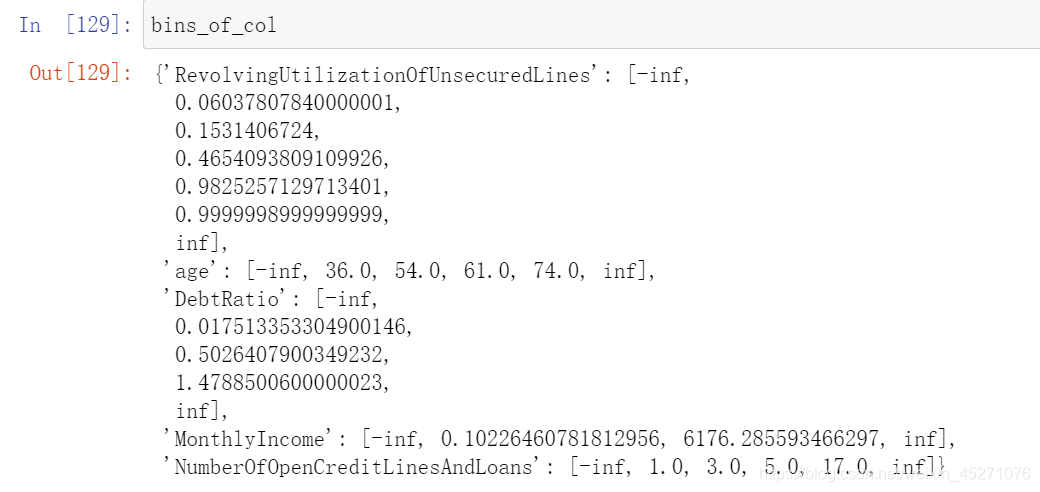
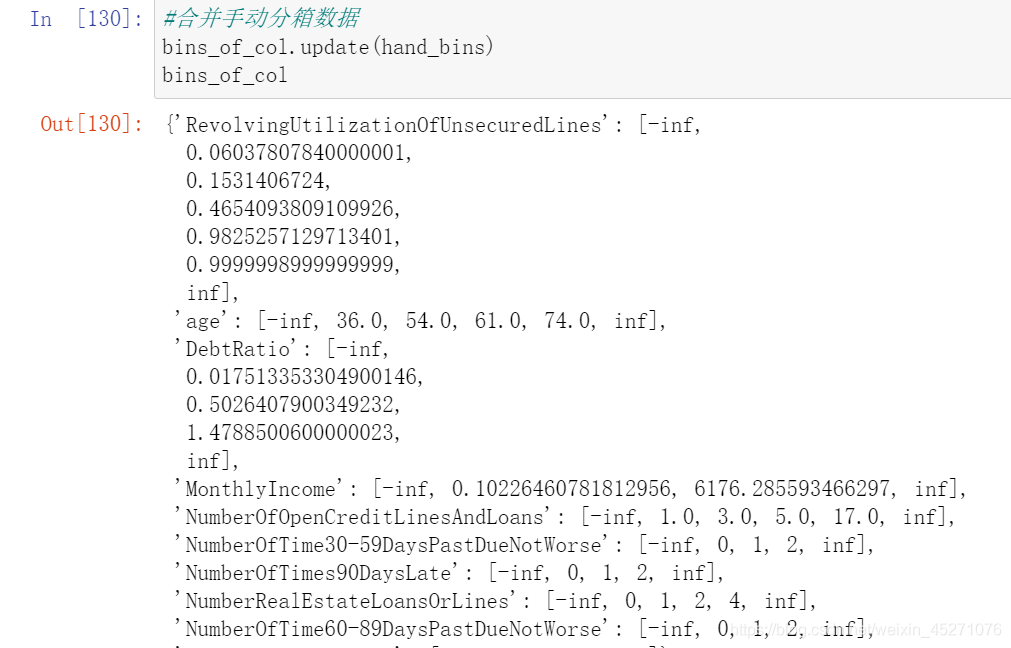
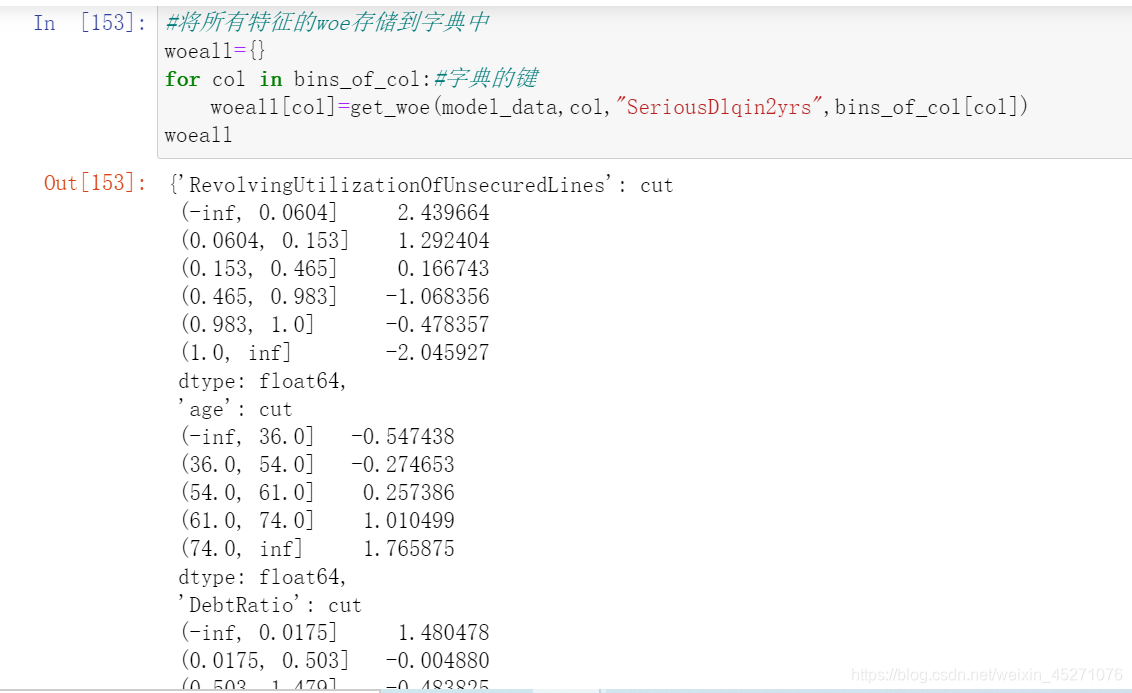
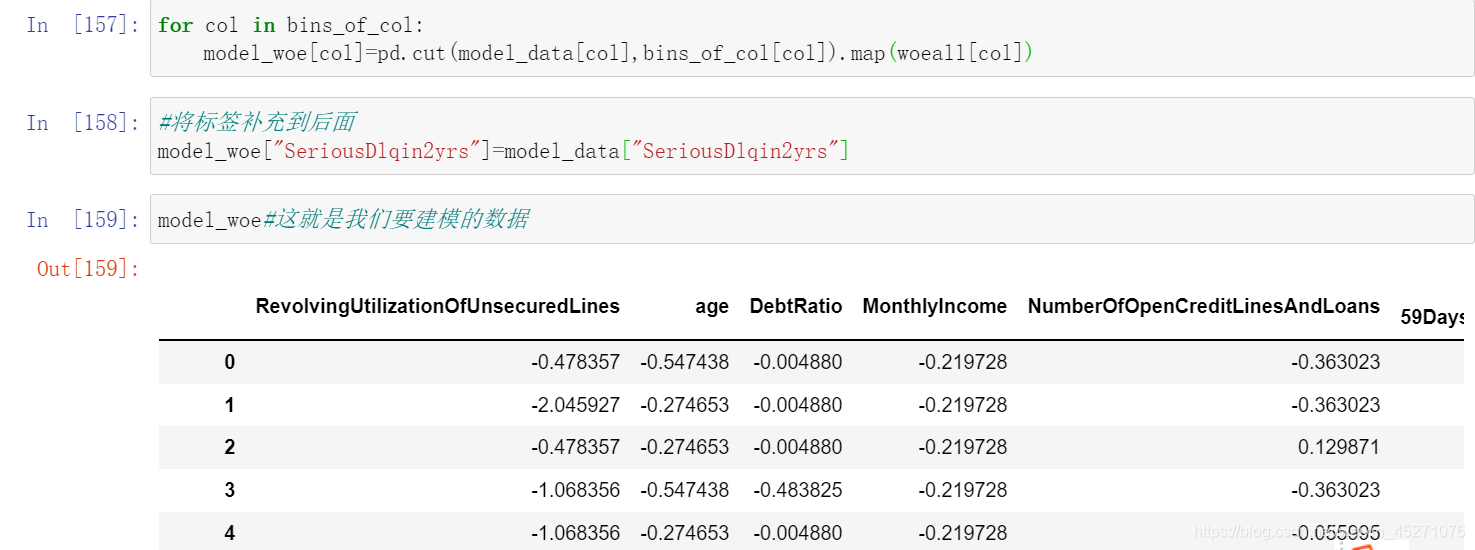
#计算每个箱子的WOE，WOE表示的是这个箱子上不违约的人的概率， #用woe代表每个箱子的不同，替换原数据，进行建模，逻辑回归是每个箱子的评分结果，分箱的结果是区间，模型无法计算 #所以采用woe来代替 #pd.qcut:是等频分箱，cut可以采用我们自己输入的区间进行分箱 data=model_data.copy()

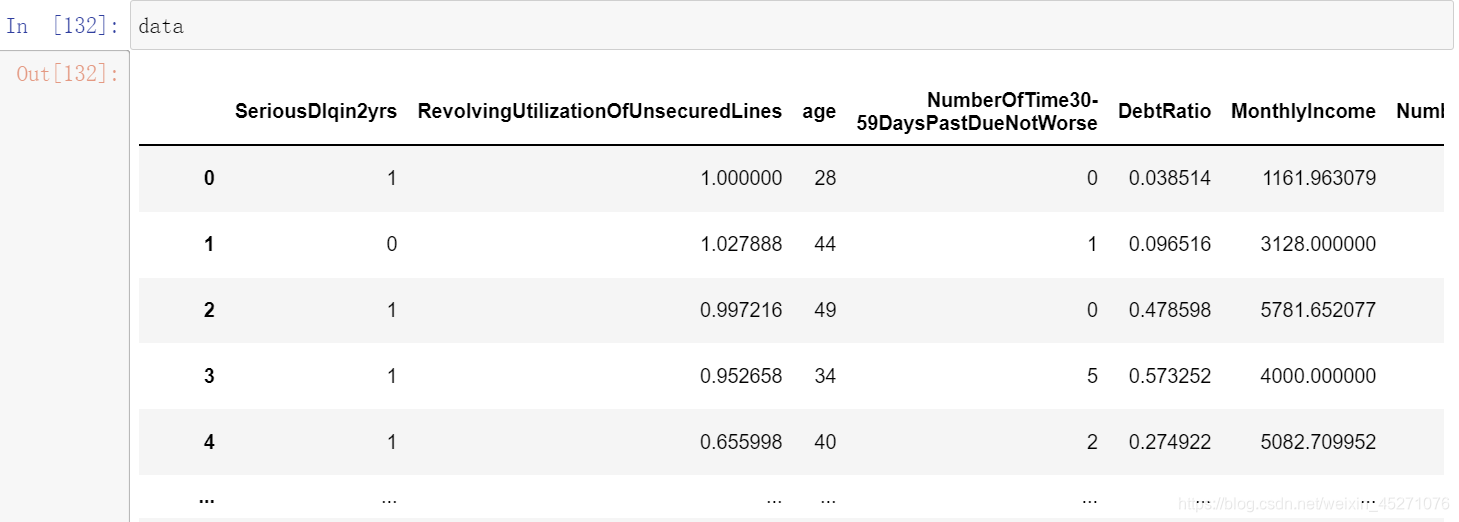
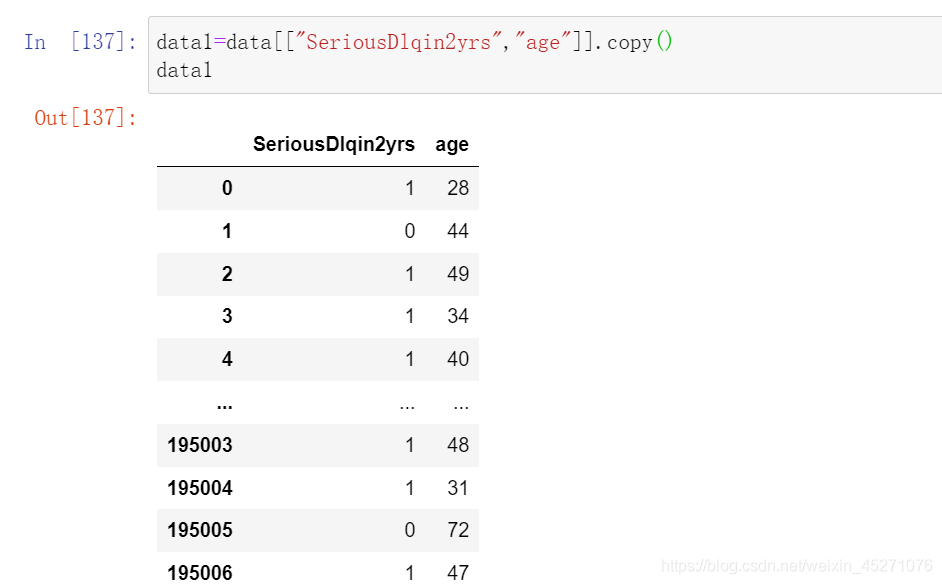
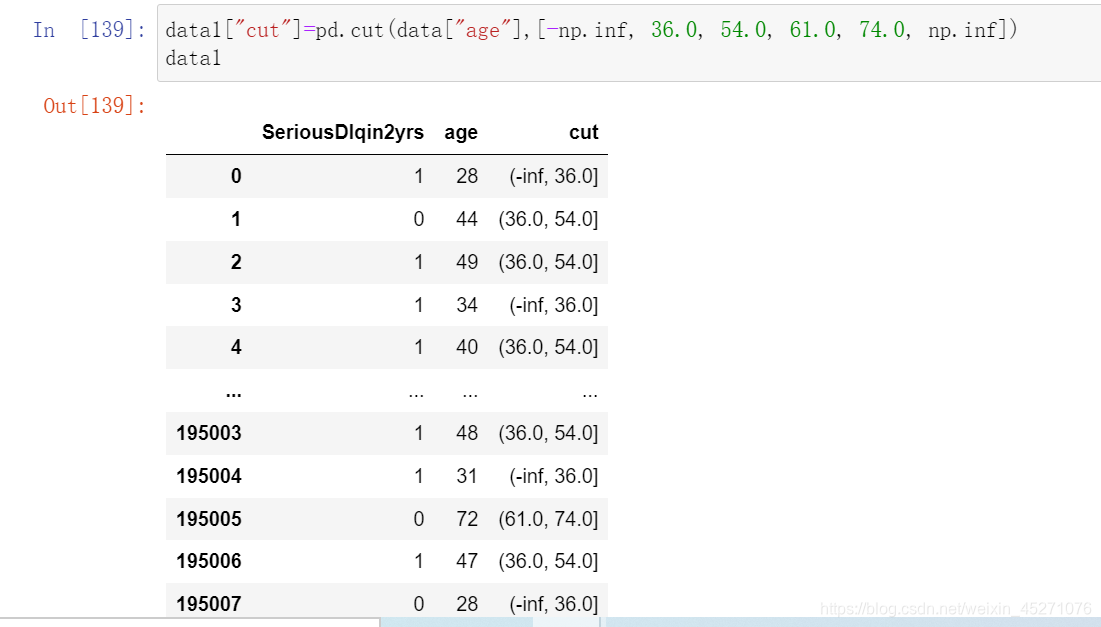
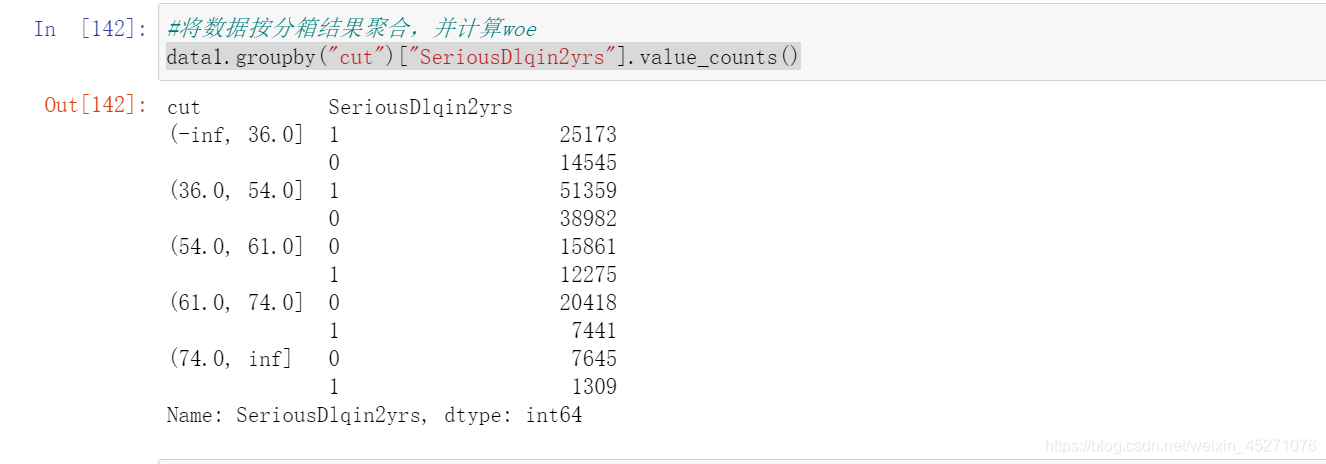
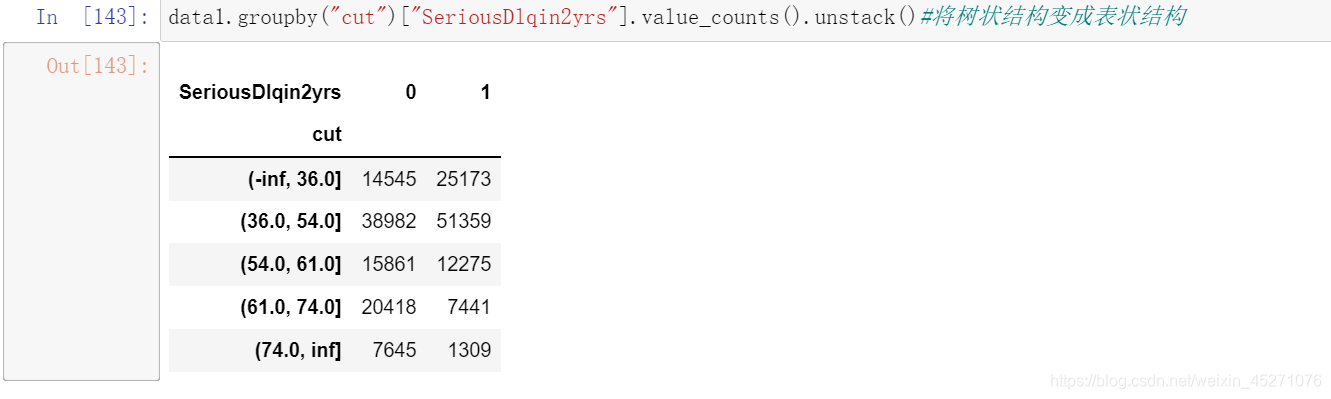
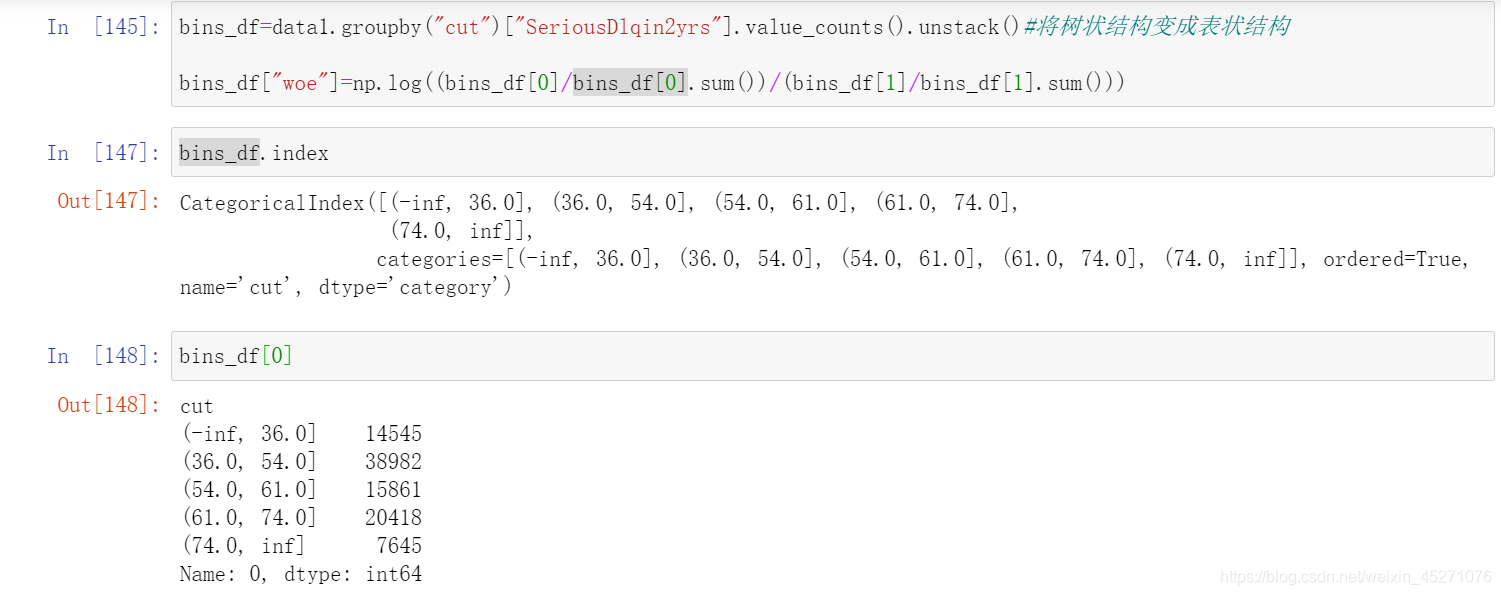
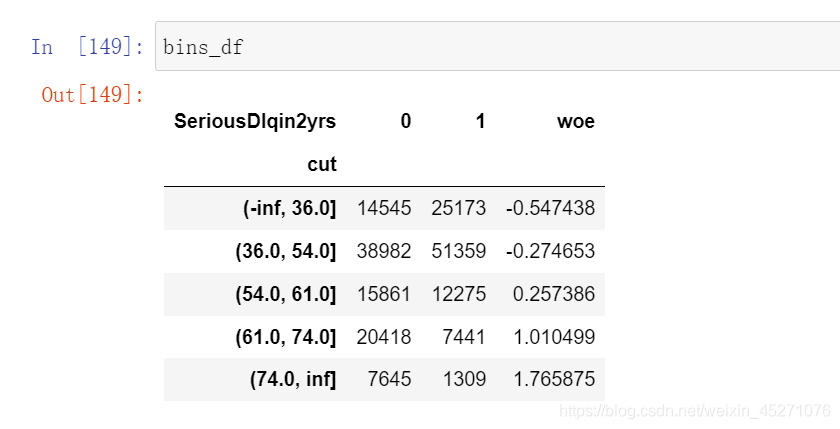
#把上述计算woe的包装成函数
def get_woe(df,col,y,bins):df=df[[col,y]].copy()#col是要分箱的那一列，bins是分箱的区间，y是标签df["cut"]=pd.cut(df[col],bins)#把给定的那一列按照bins间隔进行分箱bins_df=df.groupby("cut")[y].value_counts().unstack()woe=bins_df["woe"]=np.log((bins_df[0]/bins_df[0].sum())/(bins_df[1]/bins_df[1].sum()))return woe
#

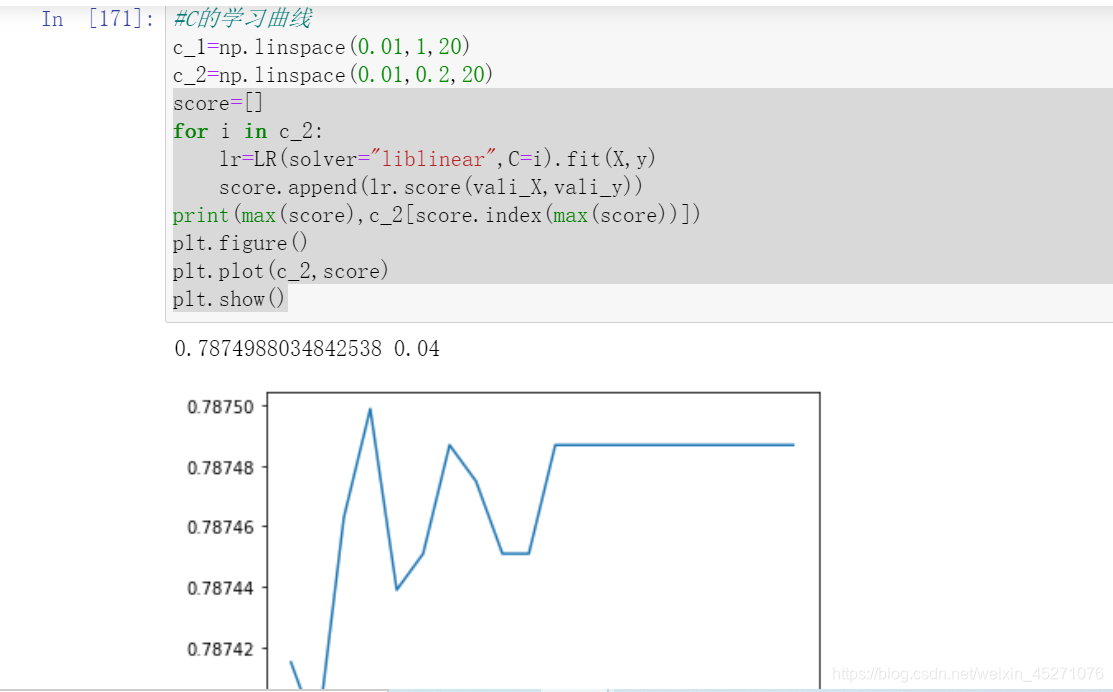
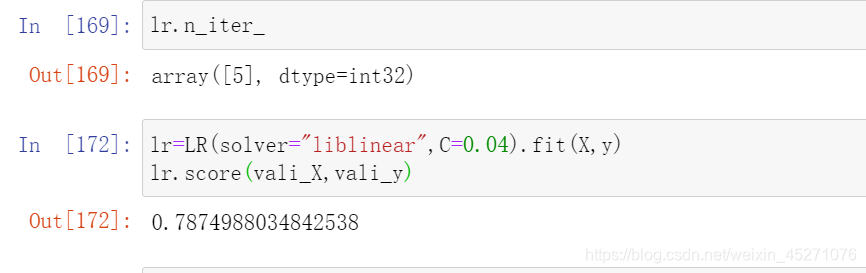
score=[]
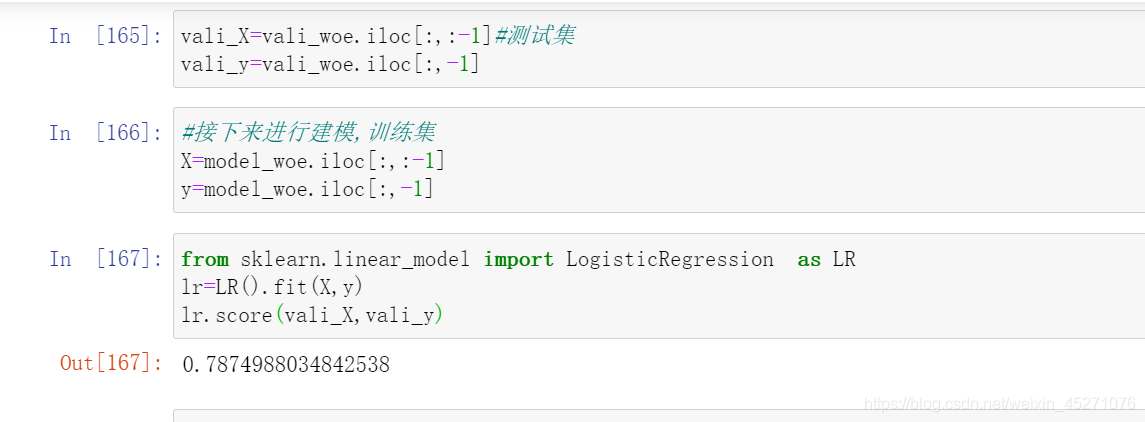
for i in [1,2,3,4,5,6]:lr=LR(solver="liblinear",C=0.04,max_iter=i).fit(X,y)score.append(lr.score(vali_X,vali_y))
plt.figure()
plt.plot([1,2,3,4,5,6]score=[]
for i in c_2:lr=LR(solver="liblinear",C=i).fit(X,y)score.append(lr.score(vali_X,vali_y))
print(max(score),c_2[score.index(max(score))])
plt.figure()
plt.plot(c_2,score)
plt.show(),score)
plt.show() 

#准确率不高，换个模型评估指标，使用ROC曲线
import scikitplot as skplot
vali_proba_df=pd.DataFrame(lr.predict_proba(vali_X))
skplot.metrics.plot_roc(vali_y,vali_proba_df,plot_micro=False,figsize=(6,6))

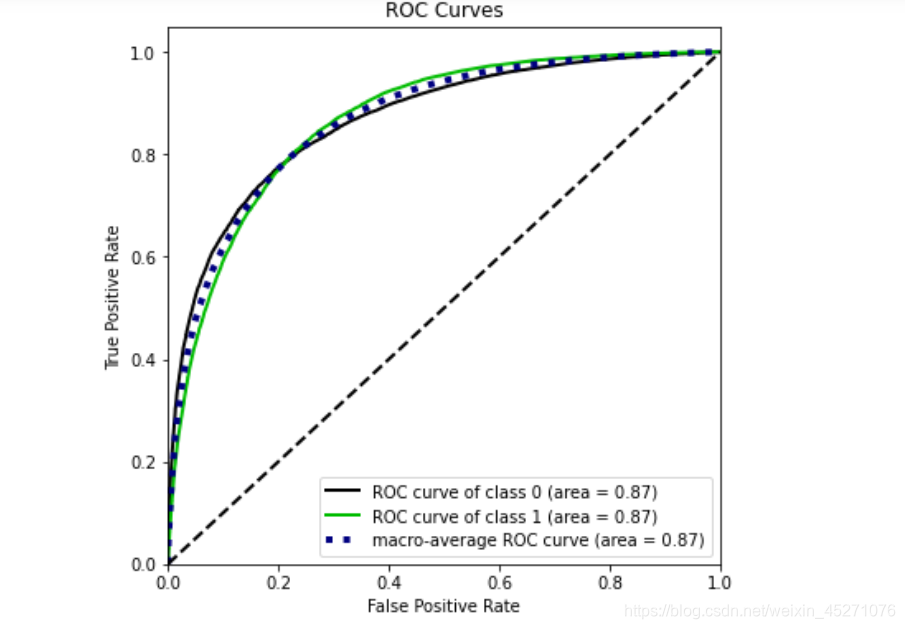
ROC反应的是当对少数类进行判断时，付出的代价，AUC面积越大效果越好，
虽然精确度不高，AUC-0.94说明模型在捕捉少数类的能力很好

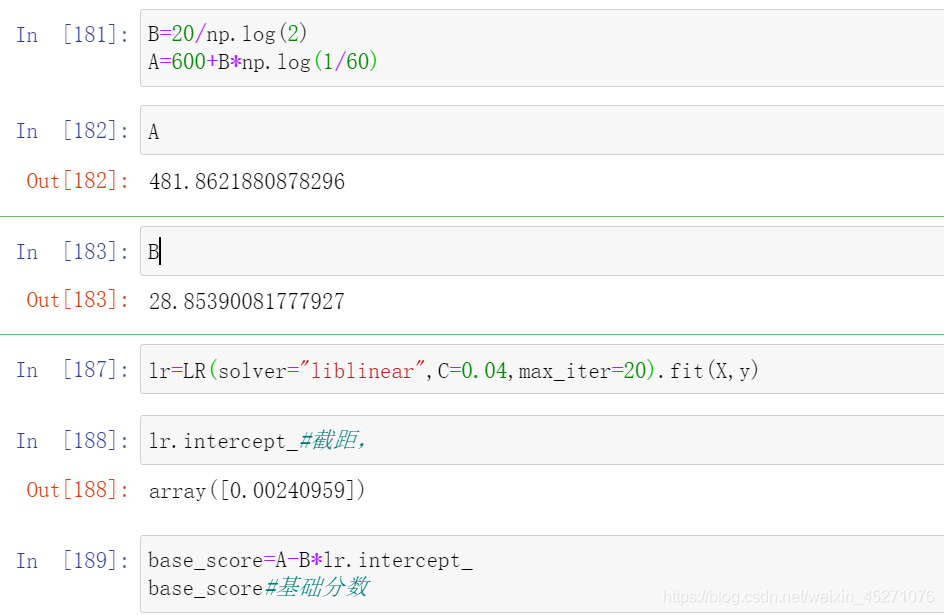
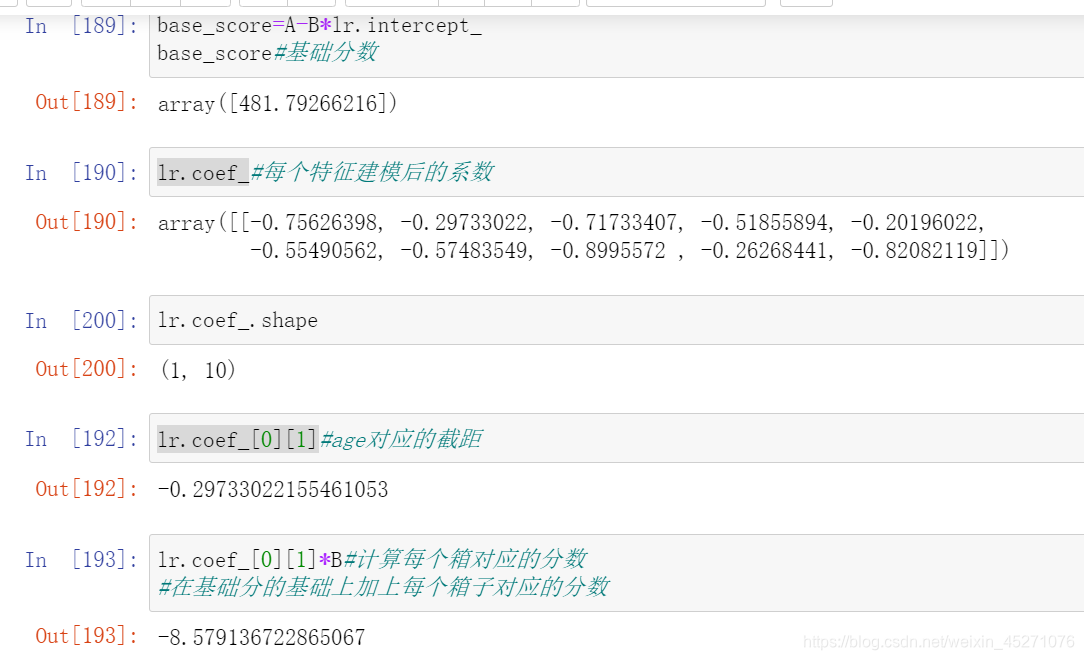
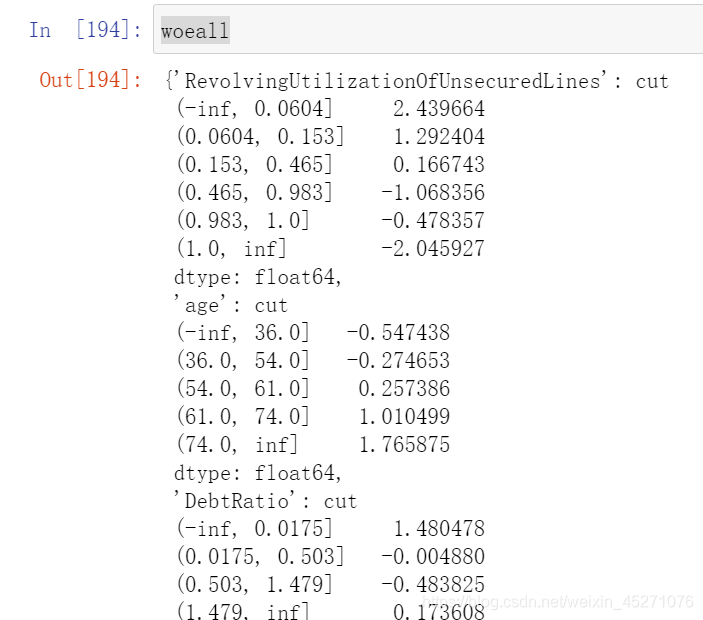
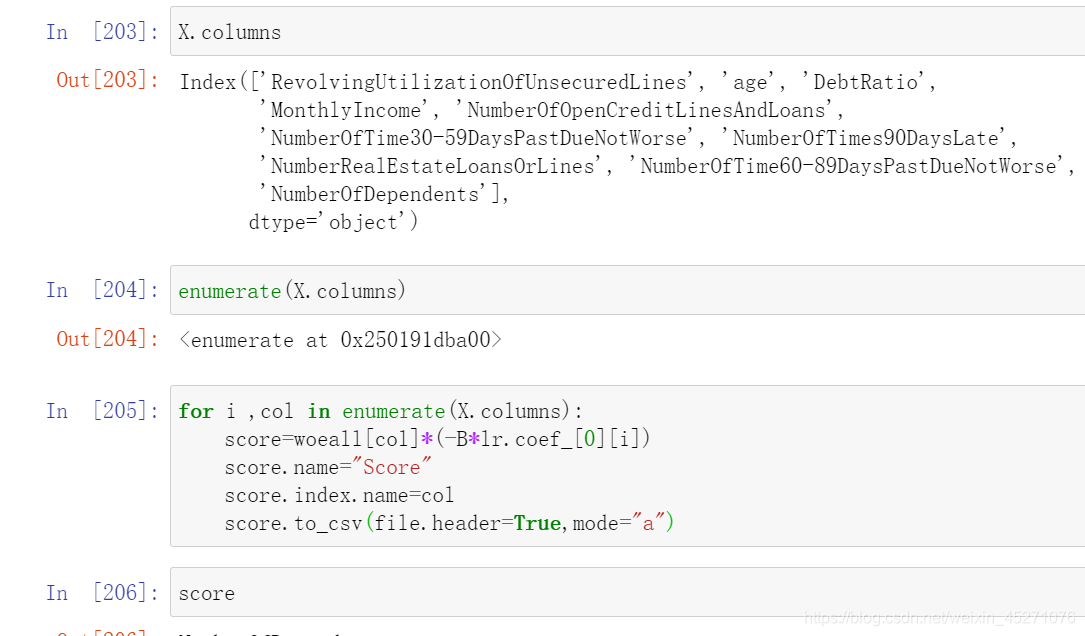
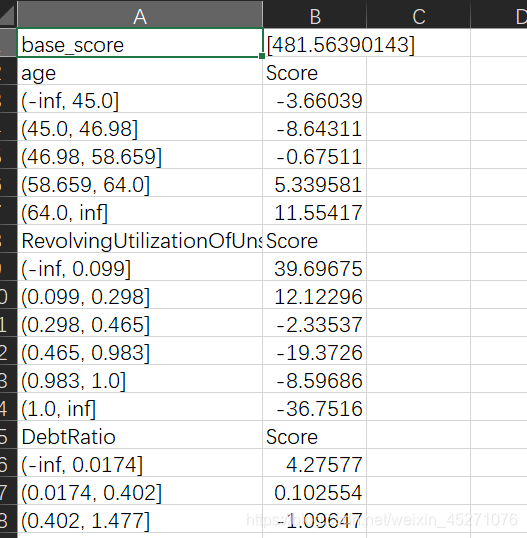
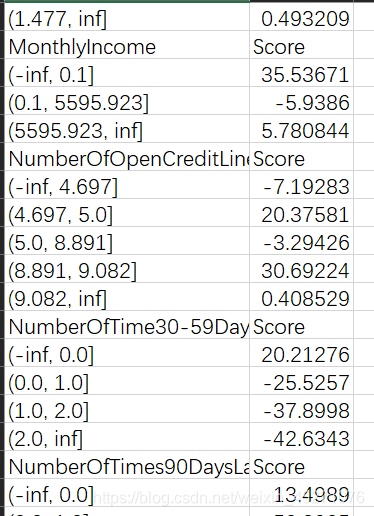
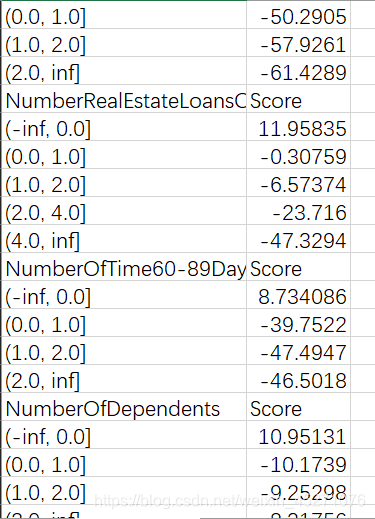最终得到的结果是每个箱子的分数 ，当客户来填资料的时候，每一个特征会落到每一个箱子中，基础分加上所有特征的对应箱子的分数，就能得到最终客户的评分