wordpress栏目页调用内容北京网站优化seo
在2014年终总结中,我提到要对这学期学过的数学课中的部分算法进行仿真实现。《数值分析》和《工程优化》这两门数学课里面还有些专门讲算法的,可以用来仿真。在《随机过程》这门课中,几乎全都是公式推导,定理证明,实在难以仿真实现。最后发现,马尔科夫链这一章比较适合仿真,况且先前也写过类似的程序,更重要的是之前有人也问过关于马氏链的Matlab实现问题。关于马氏链的理论原理在这就不作描述,下面直接用程序来实现具体问题的求解。
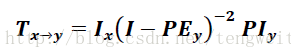

假设有9个状态,其状态转移图如下所示:
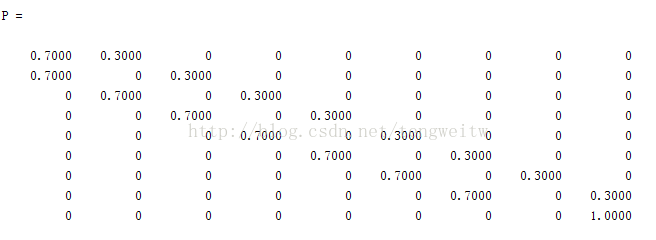
根据状态转移图,我们可以得到其一步转移概率矩阵为P:

问题一:从状态1在1000次内转移到状态9的概率为多少?
理论值:
由一步转移概率矩阵P的性质知,P的n次幂矩阵Pn中的第i行第j列的元素表示的是从状态i经过n步转移到状态j的概率。注意到,状态9为吸收态。因此,在1000步以内的任意一步到达状态9后,就永远停留在了状态9。所以P的1000次幂矩阵P1000中的第1行第9列就是从状态1在1000次内转移到状态9的概率。
仿真值:
在仿真中,我们设置仿真次数为100000次(越大越好),设置初始状态为1,在1000步中,如果到达状态9就记录,然后跳出循环,开始新一轮循环。具体代码如下:
clear all
clc%一步转移概率矩阵
P=[0.7 0.3 0 0 0 0 0 0 00.7 0 0.3 0 0 0 0 0 00 0.7 0 0.3 0 0 0 0 0 0 0 0.7 0 0.3 0 0 0 0 0 0 0 0.7 0 0.3 0 0 0 0 0 0 0 0.7 0 0.3 0 0 0 0 0 0 0 0.7 0 0.3 0 0 0 0 0 0 0 0.7 0 0.3 0 0 0 0 0 0 0 0 1];p=P^1000;
p(1,9)%理论值
num=0;%记录到达状态9的次数
for i=1:100000%实验次数state=1;%初始状态为1for j=1:1000%1000步if state==1if rand()<0.3state=2;endelseif state==9state=9;elseif rand()<0.3state=state+1;elsestate=state-1;endendif state==9num=num+1;break;endend
end num/100000 %仿真值问题二:从状态1到状态9平均需要几步?
理论值:
最直观的想法就是:假设从状态1到达状态9需要n步的概率为pn,则平均步数可以表示为1*p1+2*p2+……+n*pn+……。注意,这里的pn是首达概率,即从状态1经过k步首次到达状态9的概率,也就是前k-1次没有到达状态9。显然这里的首达概率而不是转移概率矩阵中的概率。这里的首达概率不好求,不过可以矩阵论(可惜没有选这门课)的相关知识来理论求解,最终可以得到的表达式如下:
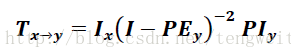
其中,x,y表示状态,在本例中,x=1,y=9,其它符号表示如下:

仿真值:
有时候,理论比较复杂的问题,仿真起来就相对简单,和问题一中的仿真类似,假定仿真次数为10000次,设置最大步数为100000000,当到达状态9时,就记录所需步数并跳出循环,具体的程序实现如下:
clear all
clcP=[0.7 0.3 0 0 0 0 0 0 00.7 0 0.3 0 0 0 0 0 00 0.7 0 0.3 0 0 0 0 0 0 0 0.7 0 0.3 0 0 0 0 0 0 0 0.7 0 0.3 0 0 0 0 0 0 0 0.7 0 0.3 0 0 0 0 0 0 0 0.7 0 0.3 0 0 0 0 0 0 0 0.7 0 0.3 0 0 0 0 0 0 0 0 1];sum=0;
p=P^1000;x=1;
y=9;
P_size=9;%状态个数
Ix=zeros(1,P_size);%行向量
Ix(x)=1;
Iy=zeros(P_size,1);%列向量
Iy(y)=1;
I=eye(P_size);
Ey=I;
Ey(y,y)=0;average=Ix*(I-P*Ey)^-2*P*Iy%理论值state=1;%初始状态
num=0;%达到次数
result=0;%需要经过的步数
for k=1:100000%仿真10000次state=1;for i=1:100000000%设定最大步数(越大越好)if state==1if rand()<0.3state=2;endelseif state==9state=9;elseif rand()<0.3state=state+1;elsestate=state-1;endendif state==9num=num+1;result=result+i;%记录总的步数break;endend
end result/num%计算平均步数原文:http://blog.csdn.net/tengweitw/article/details/43160553
作者:nineheadedbird

