1 简介

1.1 回溯算法原理

回溯法按深度优先策略搜索问题的解空间树。首先从根节点出发搜索解空间树，当算法搜索至解空间树的某一节点时，先利用剪枝函数判断该节点是否可行（即能得到问题的解）。如果不可行，则跳过对该节点为根的子树的搜索，逐层向其祖先节点回溯；否则，进入该子树，继续按深度优先策略搜索。

回溯法的基本行为是搜索，搜索过程使用剪枝函数来为了避免无效的搜索。剪枝函数包括两类：1. 使用约束函数，剪去不满足约束条件的路径；2.使用限界函数，剪去不能得到最优解的路径。

问题的关键在于如何定义问题的解空间，转化成树（即解空间树）。解空间树分为两种：子集树和排列树。两种在算法结构和思路上大体相同。

当问题是要求满足某种性质（约束条件）的所有解或最优解时，往往使用回溯法。它有“通用解题法”之美誉。

1.2 重要概念

回溯法的实现方法有两种：递归和递推（也称迭代）。一般来说，一个问题两种方法都可以实现，只是在算法效率和设计复杂度上有区别。

子集树：所给的问题是从n个元素的集合S中找出满足某种性质的子集时，相应的解空间成为子集树。也可以理解成组合问题，选取到的样本是无序的。
排列树：所给的问题是确定n个元素满足某种性质的排列时，相应的解空间就是排列树。也可以理解成排列问题，选取的样本考虑排序。

2 回溯算法实战

我将用LeetCode上的几道题目来帮助大家理解回溯算法：

• LeetCode 22: 括号生成
• LeetCode 46: 全排列
• LeetCode 77: 组合
• LeetCode 131: 分割回文串

2.1 括号生成

2.1.1 题目

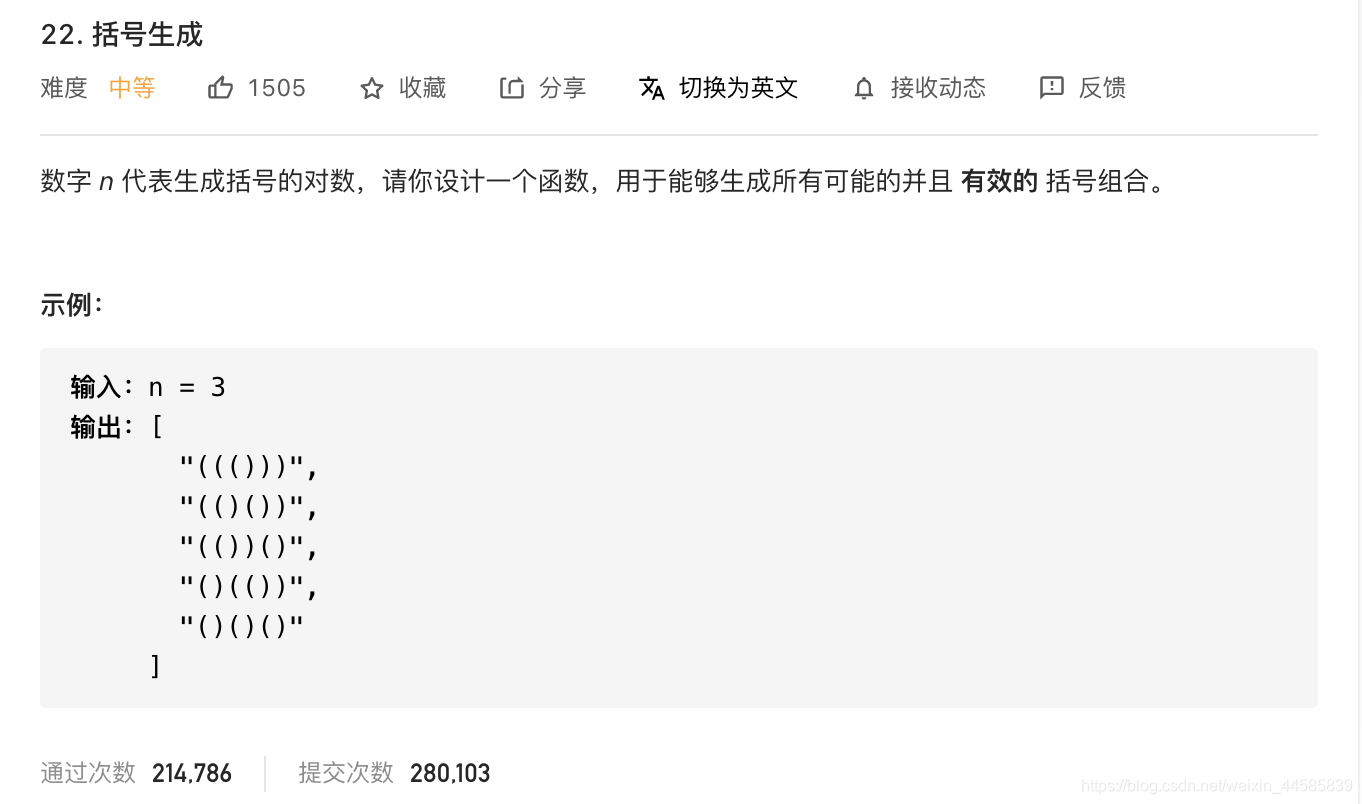
2.1.2 思路

很经典的回溯题目，该问题可以设计成排列树，采用DFS进行搜索。其剪枝条件有三：

• 右括号数量为n时，结束
• 左括号数量可以随便增加，但不超过n
• 右括号数量可以增加，但不能超过左括号数量或n

2.1.3 代码

class Solution:def generateParenthesis(self, n: int) -> List[str]:# 初始两个计数器，left是左括号计数器，right是右括号计数器left = 0right = 0res = [] def dfs(left, right, parttern):if right == n:res.append(parttern)if left < n:dfs(left + 1, right, parttern + '(')if right < n and right < left:dfs(left, right + 1, parttern + ')')dfs(0, 0, '')return res

2.1.4 结果

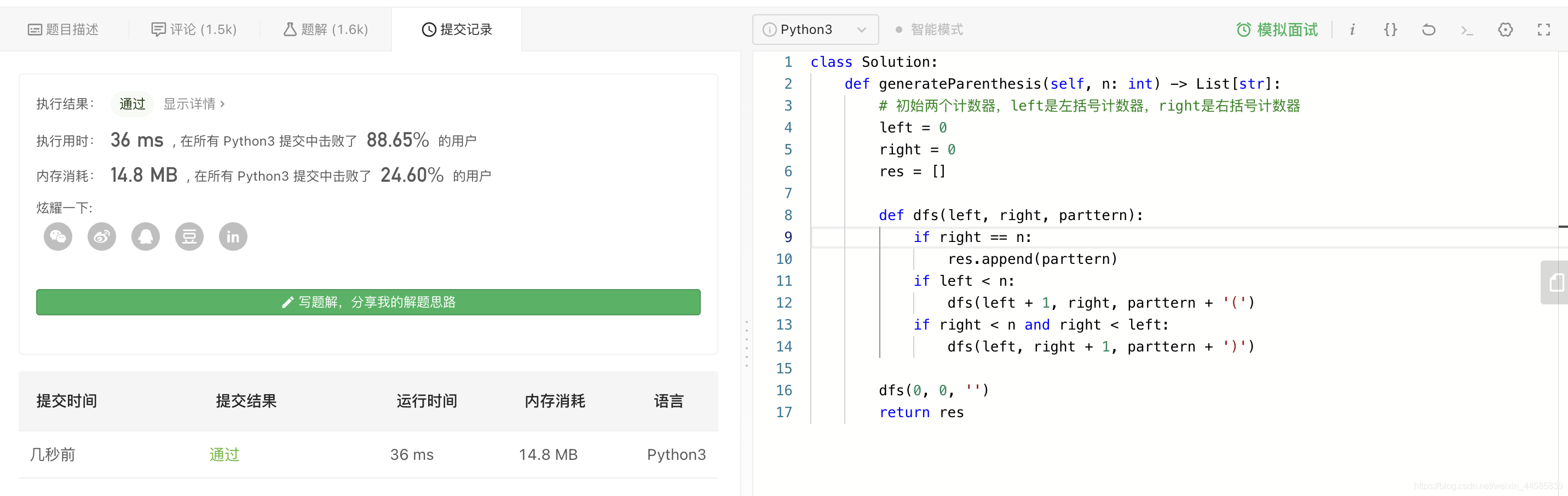
2.2 全排列

2.2.1 题目

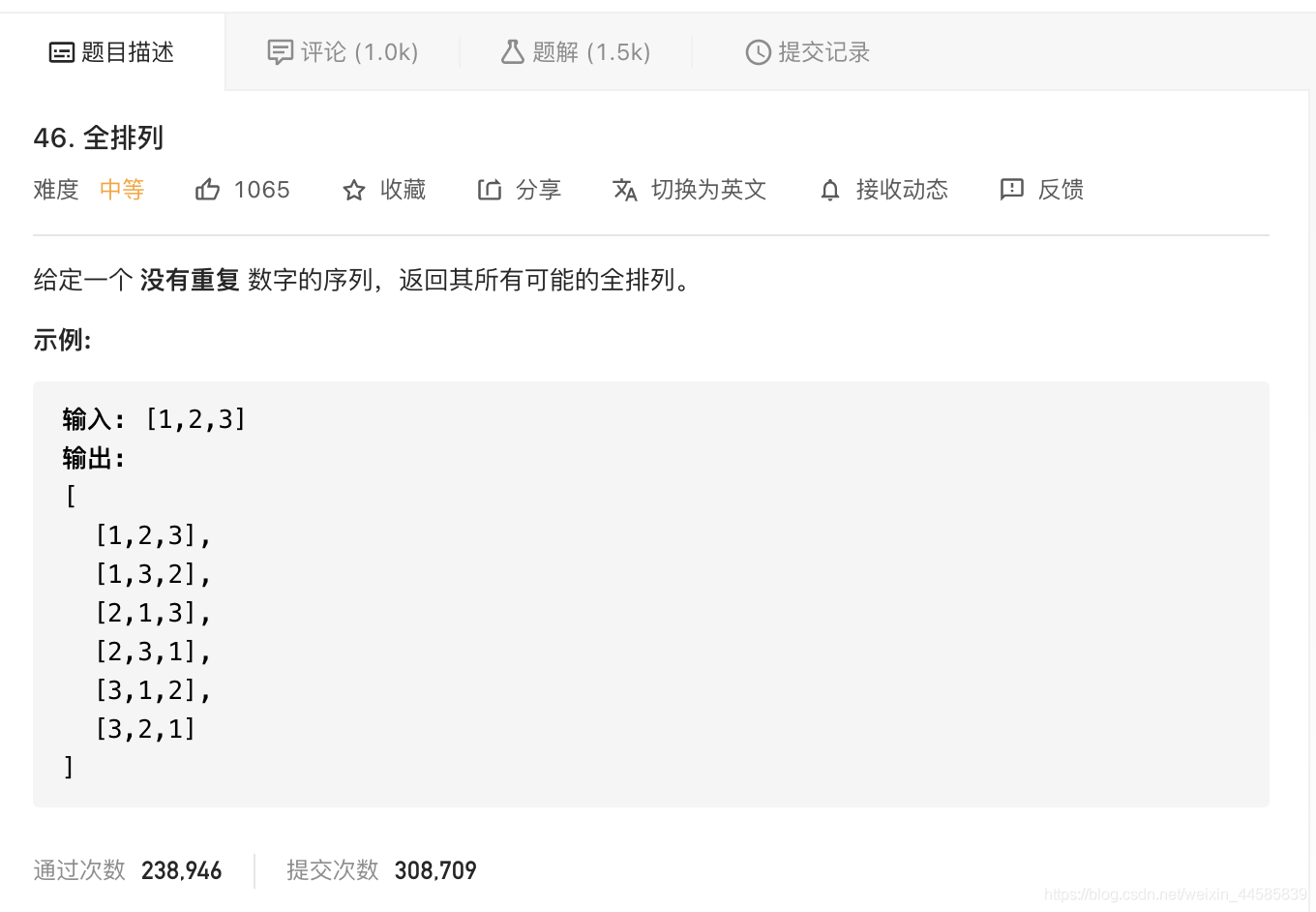
2.2.2 思路

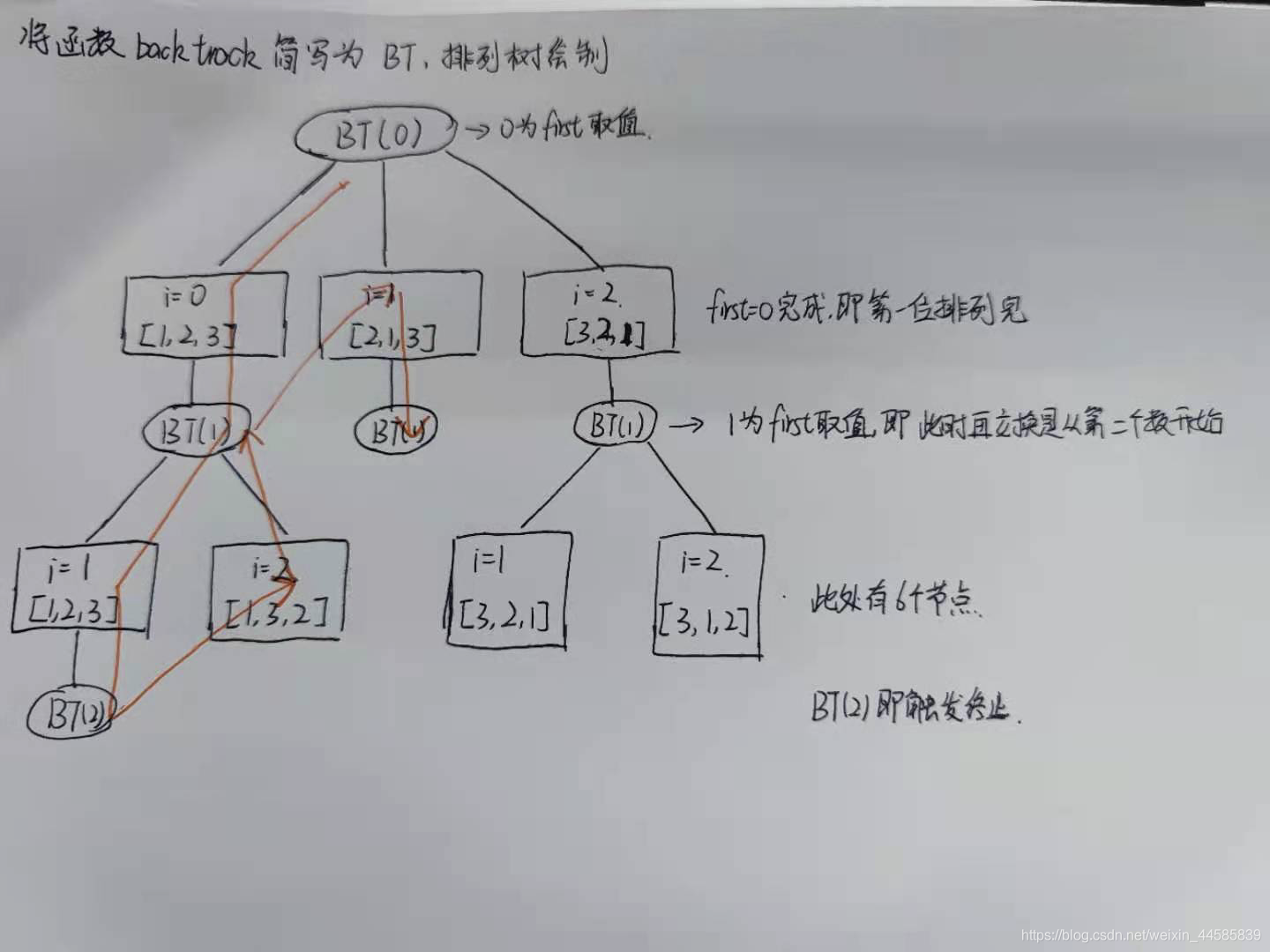
回溯，使用的排列树的算法，为了方便理解我将该排列树绘制出来。该算法的思路为：

1. first为排序指针，first左侧是已经完成排序。
2. 数组维护：这里排列是采用交换nums，每次回溯完都会交换回来。同样，在触发终止条件时需要用nums[:]进行拷贝存储。
3. 终止条件：first为n-1或n。n-1之所以可以停止是因为排列好n-1个，最后一个也就确定下来了。
4. 遍历类型：下面图中我采用一种特殊颜色的笔绘制了排列路径，是DFS。

2.2.3 代码

class Solution:def permute(self, nums):def backtrack(first = 0):# n-1触发终止，前n-1确定后最后一位不用考虑# 也可以将终止条件写成nif first == n-1:  res.append(nums[:])for i in range(first, n):# 动态维护数组nums[first], nums[i] = nums[i], nums[first]# 继续递归填下一个数backtrack(first + 1)# 撤销操作nums[first], nums[i] = nums[i], nums[first]n = len(nums)res = []backtrack()return res

2.2.4 结果

2.3 组合

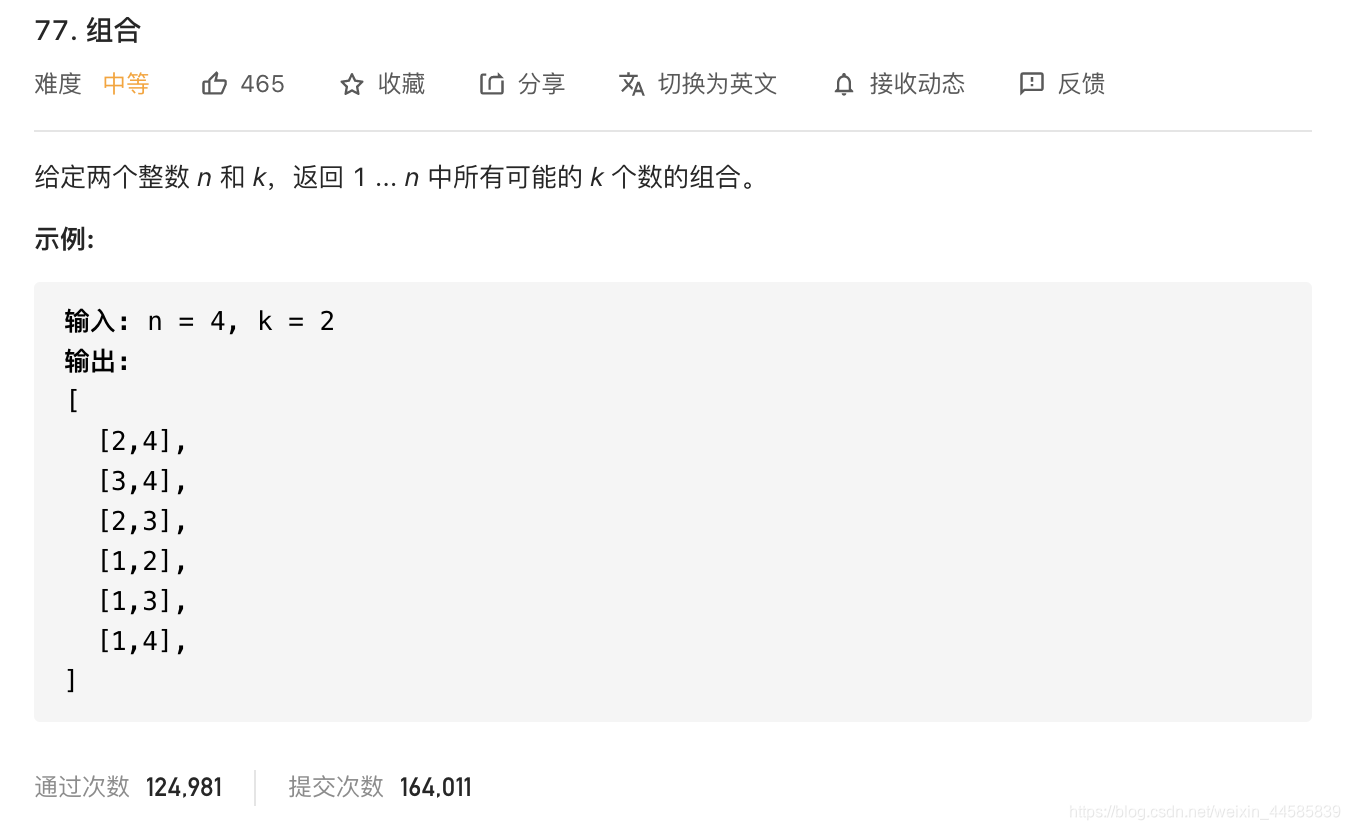
2.3.1 题目

2.3.2 思路

回溯法，采用DFS方法，具体实现思路为：

1. 从n中选择k个分两种情况，第一种是选择第k个再从剩下的n-1中选择k-1个，第二种是不选择第k个从剩下n-1中选择k-1个。即dfs(n,k) = dfs(n-1,k) + dfs(n-1,k-1)
2. 退出：k == 1或k==n时

2.3.3 代码

class Solution:def combine(self, n: int, k: int) -> List[List[int]]:# 回溯：dfs(n,k) = dfs(n-1,k) + dfs(n-1,k-1) def dfs(n, k):if k>n or k==0:return []if k==1:return [[i] for i in range(1,n+1)]if k==n:return [[i for i in range(1,n+1)]]answer=dfs(n-1,k)for item in dfs(n-1,k-1):item.append(n)answer.append(item)return answerres = dfs(n, k)return res

2.3.4 结果

2.4 分割回文串

2.4.1 题目

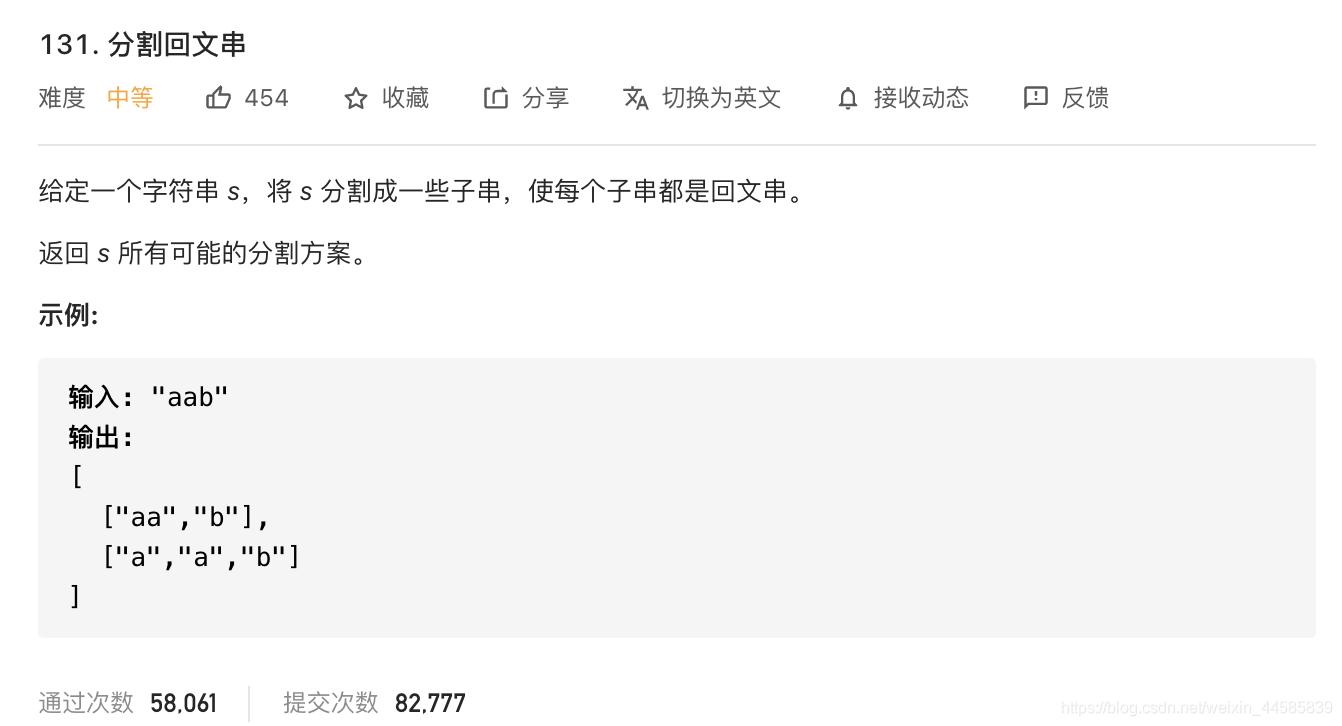
2.4.2 思路

经典回溯，DFS实现，绘制了一下回溯树帮助大家理解。

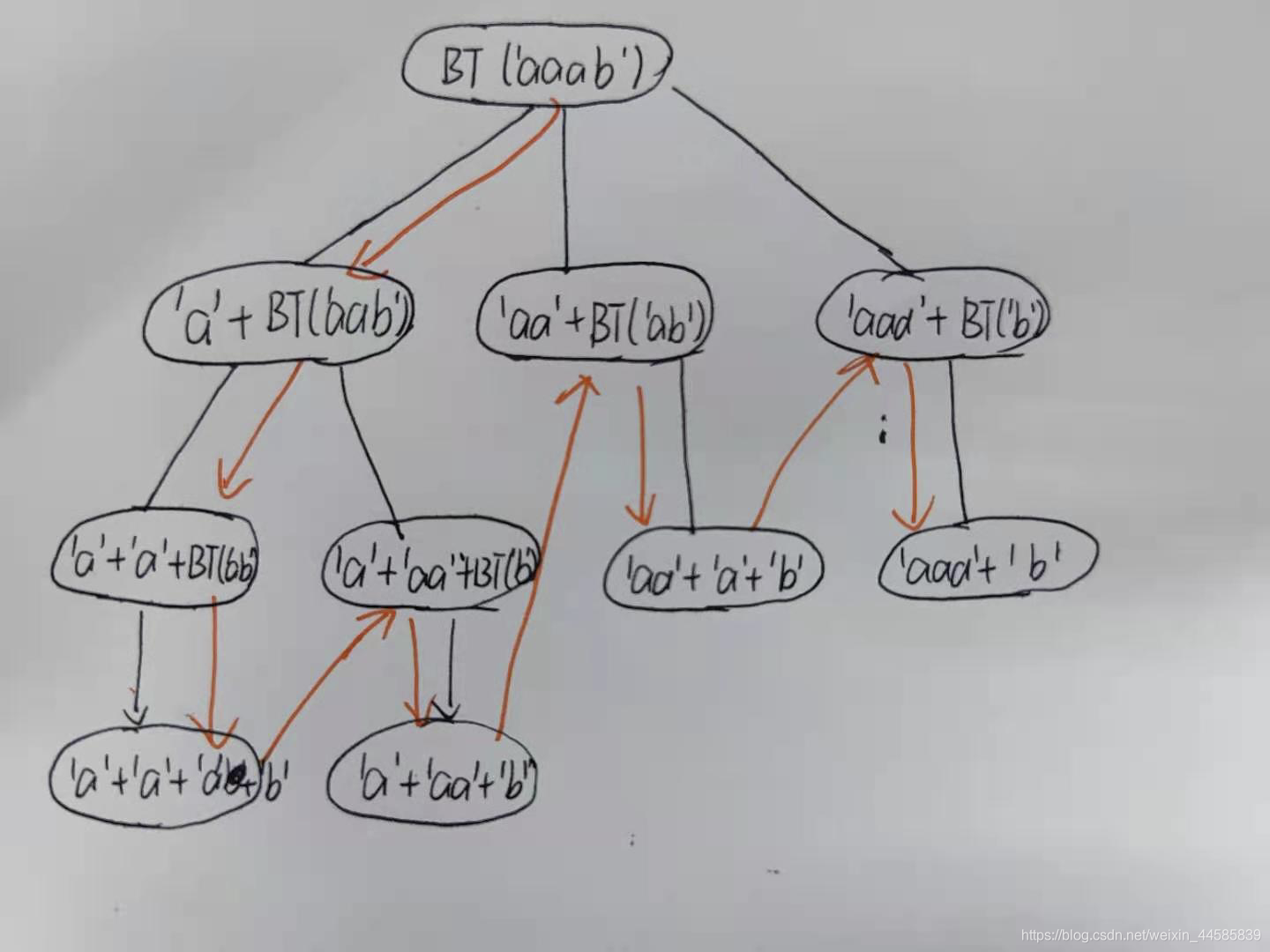
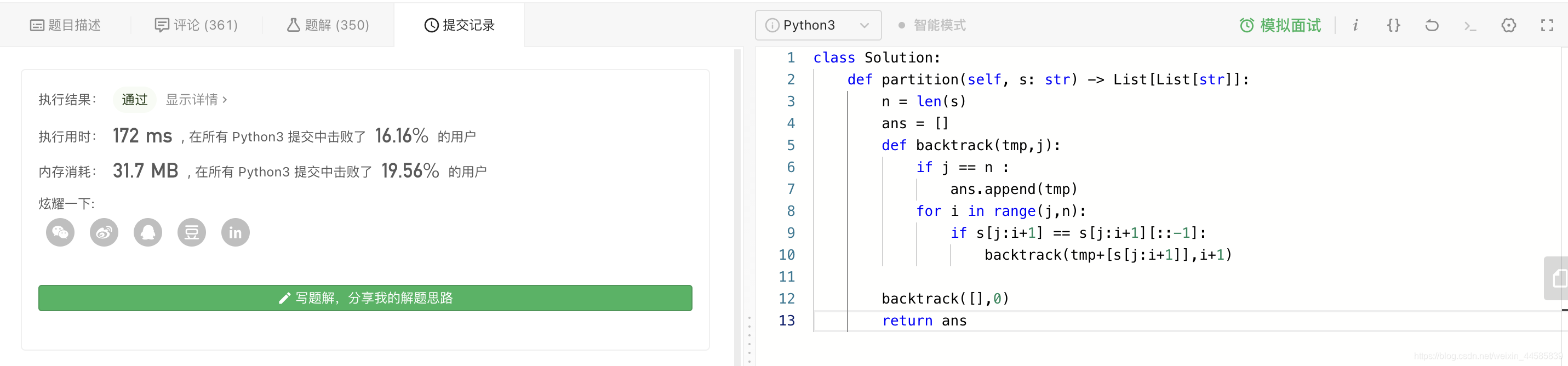
2.4.3 代码

class Solution:def partition(self, s: str) -> List[List[str]]:n = len(s)ans = []def backtrack(tmp,j):if j == n :ans.append(tmp)for i in range(j,n):if s[j:i+1] == s[j:i+1][::-1]:backtrack(tmp+[s[j:i+1]],i+1)backtrack([],0) return ans

2.4.4 结果