定义
连通图:在无向图中,若任意两个顶点vivi与vjvj都有路径相通,则称该无向图为连通图。
强连通图:在有向图中,若任意两个顶点vivi与vjvj都有路径相通,则称该有向图为强连通图。
连通网:在连通图中,若图的边具有一定的意义,每一条边都对应着一个数,称为权;权代表着连接连个顶点的代价,称这种连通图叫做连通网。
生成树:一个连通图的生成树是指一个连通子图,它含有图中全部n个顶点,但只有足以构成一棵树的n-1条边。一颗有n个顶点的生成树有且仅有n-1条边,如果生成树中再添加一条边,则必定成环。
最小生成树:在连通网的所有生成树中,所有边的代价和最小的生成树,称为最小生成树。
kruskal算法
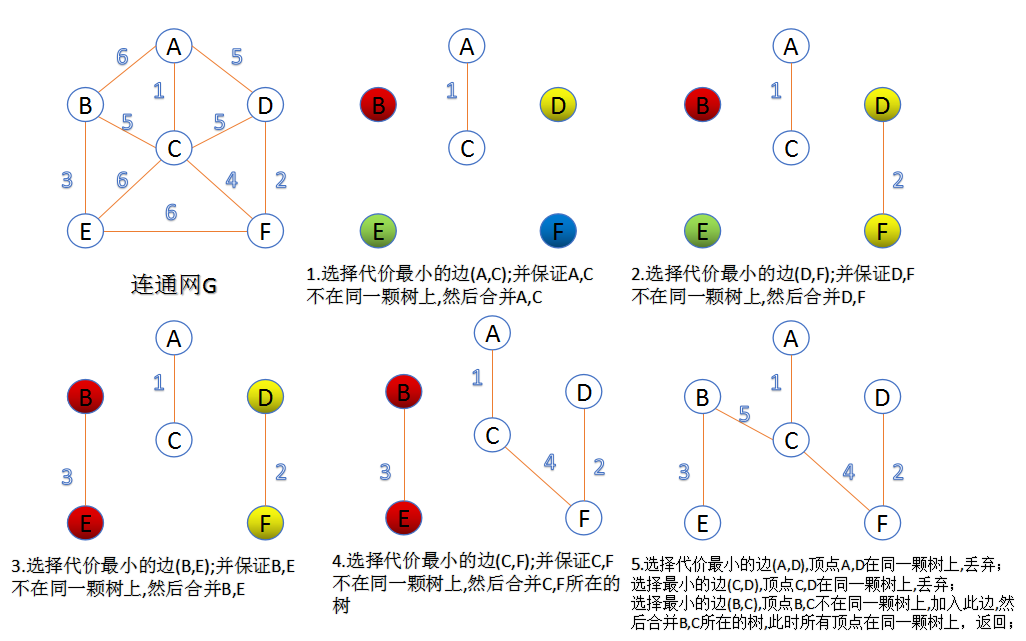
此算法可以称为“加边法”,初始最小生成树边数为0,每迭代一次就选择一条满足条件的最小代价边,加入到最小生成树的边集合里。
1. 把图中的所有边按代价从小到大排序;
2. 把图中的n个顶点看成独立的n棵树组成的森林;
3. 按权值从小到大选择边,所选的边连接的两个顶点ui,viui,vi,应属于两颗不同的树,则成为最小生成树的一条边,并将这两颗树合并作为一颗树。
4. 重复(3),直到所有顶点都在一颗树内或者有n-1条边为止。
prim算法
此算法可以称为“加点法”,每次迭代选择代价最小的边对应的点,加入到最小生成树中。算法从某一个顶点s开始,逐渐长大覆盖整个连通网的所有顶点。
1. 图的所有顶点集合为VV;初始令集合u={s},v=V−uu={s},v=V−u;
2. 在两个集合u,vu,v能够组成的边中,选择一条代价最小的边(u0,v0)(u0,v0),加入到最小生成树中,并把v0v0并入到集合u中。
3. 重复上述步骤,直到最小生成树有n-1条边或者n个顶点为止。

kruskal算法:
#include <iostream>
#include <list>
#include <vector>
#include <algorithm>const int INFINITE = 0x7FFFFFFF;
const int VERTEX = 6;
const char szVertex[] = { 'A', 'B', 'C', 'D', 'E', 'F' };struct stEdge
{int u;int v;int weight;stEdge(int iu, int iv, int iweight):u(iu),v(iv),weight(iweight) {}friend bool operator<(const stEdge &a, const stEdge &b) { return a.weight < b.weight; }
};void createGraph(int (*g)[VERTEX])
{for (int i = 0; i < VERTEX; i++){for (int j = 0; j < VERTEX; j++){g[i][j] = INFINITE;}}g[0][1] = 6; g[0][2] = 1; g[0][3] = 5;g[1][0] = 6; g[1][2] = 5; g[1][4] = 3;g[2][0] = 1; g[2][1] = 5; g[2][3] = 5; g[2][4] = 6; g[2][5] = 4;g[3][0] = 5; g[3][2] = 5; g[3][5] = 2;g[4][1] = 3; g[4][2] = 6; g[4][5] = 6;g[5][2] = 4; g[5][3] = 2; g[5][4] = 6;
}void initEdges(std::vector<stEdge> &edges, const int (*g)[VERTEX])
{for (int i = 0; i < VERTEX; ++i){for (int j = i+1; j < VERTEX; ++j){edges.push_back(stEdge(i,j,g[i][j]));}}std::sort(edges.begin(), edges.end(), std::less<stEdge>());
}bool notSameTree(int u, int v, std::vector<std::list<int> > &trees)
{int uindex = -1, vindex = -1;for (int i = 0; i < VERTEX; ++i){if (std::find(trees[i].begin(), trees[i].end(), u) != trees[i].end()){uindex = i;}if (std::find(trees[i].begin(), trees[i].end(), v) != trees[i].end()){vindex = i;}}if (uindex != vindex){trees[uindex].splice(trees[uindex].end(), trees[vindex]);return true;}return false;
}void kruskal(const int (*g)[VERTEX])
{std::vector<stEdge> edges;initEdges(edges, g);std::vector<std::list<int> > trees(VERTEX);for (int i = 0; i < VERTEX; ++i){trees[i].push_back(i);}for (auto e : edges){if (notSameTree(e.u, e.v, trees)){std::cout << szVertex[e.u] << "---" << szVertex[e.v] << std::endl;}}
}int main()
{int g[VERTEX][VERTEX] = {0};createGraph(g);kruskal(g);return 0;
}
prim算法:
#include <iostream>
#include <list>
#include <vector>
#include <algorithm>const int INFINITE = 0x7FFFFFFF;
const int VERTEX = 6;
const char szVertex[] = { 'A', 'B', 'C', 'D', 'E', 'F' };struct stEdge
{int index;int weight;
};void createGraph(int (*g)[VERTEX])
{for (int i = 0; i < VERTEX; i++){for (int j = 0; j < VERTEX; j++){g[i][j] = INFINITE;}}g[0][1] = 6; g[0][2] = 1; g[0][3] = 5;g[1][0] = 6; g[1][2] = 5; g[1][4] = 3;g[2][0] = 1; g[2][1] = 5; g[2][3] = 5; g[2][4] = 6; g[2][5] = 4;g[3][0] = 5; g[3][2] = 5; g[3][5] = 2;g[4][1] = 3; g[4][2] = 6; g[4][5] = 6;g[5][2] = 4; g[5][3] = 2; g[5][4] = 6;
}int minIndex(const stEdge *weightArr, int len)
{int min = INFINITE;int idx = -1;for (int i = 0; i < len; ++i){if (weightArr[i].weight != 0 && min > weightArr[i].weight){min = weightArr[i].weight;idx = i;}}return idx;
}void prim(const int (*g)[VERTEX], int index)
{stEdge weightArr[VERTEX];weightArr[index].weight = 0;weightArr[index].index = index;for (int i = 0; i < VERTEX; ++i){if (i != index){weightArr[i].index = index;weightArr[i].weight = g[index][i];}}for (int i = 1; i < VERTEX; ++i){int nextIndex = minIndex(weightArr, VERTEX);if (nextIndex != -1){std::cout << szVertex[weightArr[nextIndex].index] << "---" << szVertex[nextIndex] << std::endl;weightArr[nextIndex].weight = 0;weightArr[nextIndex].index = nextIndex;for (int j = 0; j < VERTEX; ++j){if (weightArr[j].weight != 0 && g[nextIndex][j] < weightArr[j].weight){weightArr[j].index = nextIndex;weightArr[j].weight = g[nextIndex][j];}}}}
}int main()
{int g[VERTEX][VERTEX] = {0};createGraph(g);prim(g, 0);return 0;
}
转载自:https://blog.csdn.net/luoshixian099/article/details/51908175
