基本序列以及序列表示
单位冲激序列
单位冲激序列\(\delta[n]\)是用的最频繁的序列,定义为
\[ \delta[n]= \begin{cases} 1, \quad n=0 \\ 0, \quad 其他 \end{cases} \]
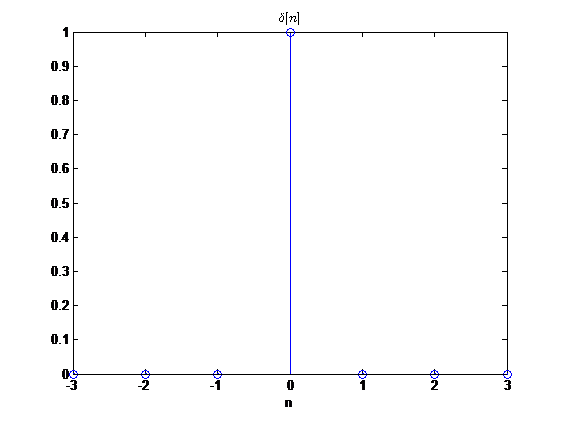
单位冲激序列经时移后的表示为
\[ \delta[n-k]= \begin{cases} 1, \quad n=k \\ 0, \quad 其他 \end{cases} \]
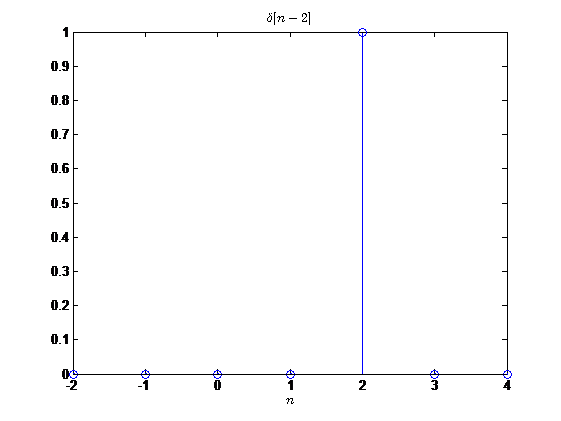
单位阶跃序列
单位阶跃序列记为\(\mu[n]\),定义为
\[ \mu[n]= \begin{cases} 1, \quad n\geq0 \\ 0, \quad n < 0 \end{cases} \]
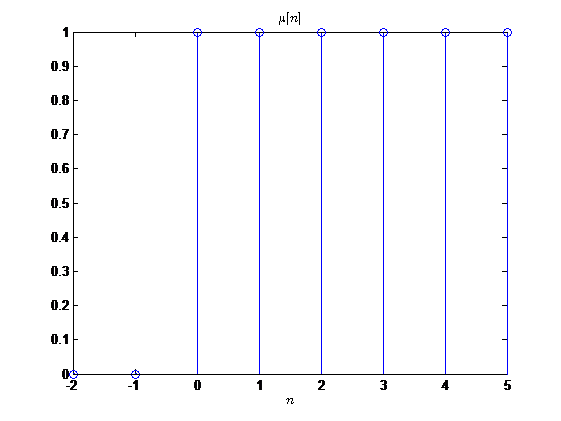
单位冲激序列与单位阶跃序列之间的关系
\[ \delta[n]=\mu[n]-\mu[n-1] \\ \mu[n]=\sum_{m=0}^{\infty} \delta[n-m]=\sum_{m=-\infty}^{n}\delta[m] \]
正弦序列
形如
\[ x[n]=Acos(w_0n+\phi),\quad -\infty<n<\infty \]
称为实正弦序列。
正弦序列的周期
由周期的定义知,若
\[ x[n+N]=x[n] \]
那么称\(N\)为序列\(x[n]\)的周期,所以有
\[ Acos(w_0(n+N)+\phi)=Acos(w_0n+\phi) \]
易知当且仅当\(w_0N=2k\pi\)等号才成立,所以有且当
\[ \frac{2\pi}{w_0}=\frac{N}{k}, \, N和k都是整数 \]
正弦序列才是周期序列,且周期为\(N\)。
也就是说,只有当\(\cfrac{2\pi}{w_0}=\frac{N}{k}\)为有理数时,正弦序列才是周期函数,这与连续信号不一样,对于连续信号,无论\(w_0\)取多少,正弦函数都是周期的。
观察下列信号是否为周期函数
\((a)x_a[n]=cos(1.5\pi n) \quad -\infty<n<\infty\\ (b)x_b[n]=cos(\sqrt3 n )\quad -\infty<n<\infty\)
解:
\((a)w_a=1.5\pi\)
则\(\cfrac{2\pi}{w_a}=\cfrac{4}{3}\)为有理数,所以序列\(x_a[n]\)为周期序列,且周期为\(4\)
\((b)w_b=\sqrt3\)
则\(\cfrac{2\pi}{w_b}=\cfrac{2\pi}{\sqrt3}\)为无理数,所以序列\(x_b[n]\)为非周期序列。
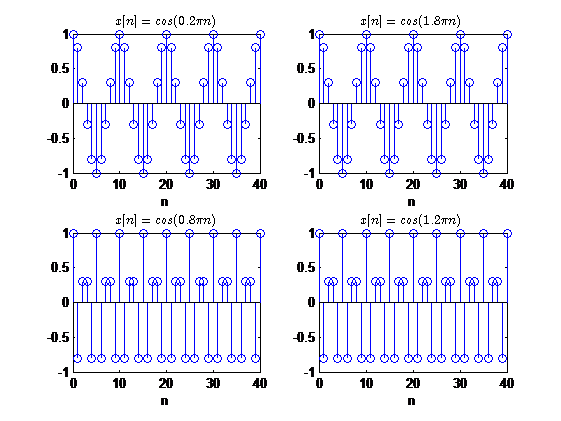
正弦序列的两个性质
性质一:
对于两个正弦序列\(x_1[n]=cos(w_1n),x_2[n]=cos(w_2n)\),其中\(0 \leq w_1 < 2\pi ,2\pi k \leq w_2 < 2\pi(k+1)\),若
\[w_2=w_1+2\pi k\]
则
\[ x_2[n]=cos((w_1+2\pi k)n)=cos(w_1n+2\pi kn)=cos(w_1n)=x_1[n] \]
无法区分这两个序列。
这个性质说明,对于任何\(w\)取值在\([0,2\pi]\)之外的正弦序列,都与\(w\)对\(2\pi\)取模得到取值的正弦序列是一样的。
比如:\(cos(3\pi n)=cos(\pi n),\,cos(2.5\pi n)=cos(0.5\pi n)\)
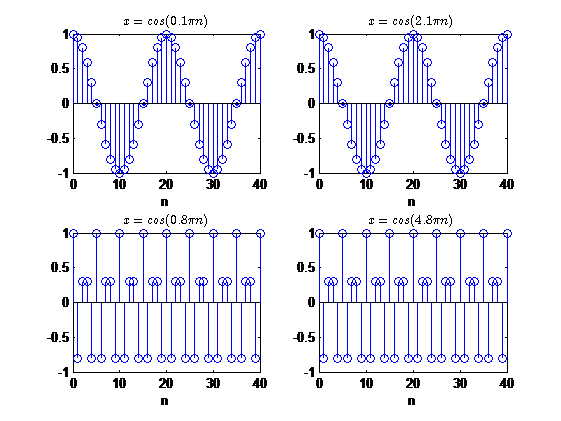
性质二:
还是考虑两个正弦序列\(x_1[n]=cos(w_1n),x_2[n]=cos(w_2n)\),其中\(0\leq w_1 < \pi,\pi \leq w_2 < 2\pi\),假设
\[w_2=2\pi-w_1\]
则
\[ x_2[n]=cos((2\pi -w_1)n)=cos(2\pi n - w_1n)=cos(-w_1n)=cos(w_1n)=x_1[n] \]
这说明对于频率为\(w\),且频率范围在\(0 \leq w < \pi\)的正弦序列,与频率为\(2\pi -w\)的正弦序列相同。于是称频率\(\pi\)为折叠频率(因为\(w\)与\(2\pi -w\)关于\(\pi\)对称)。这是正弦序列的第二个性质。
例如:\(cos(1.5\pi n)=cos(0.5\pi n)\)
指数序列
定义指数序列
\[ x[n]=A\alpha^n,\, -\infty < n < \infty \]
其中\(A\)和\(\alpha\)可以是实数,也可以是复数。
当\(A\)和\(\alpha\)都是复数时,若
\[ \alpha = e^{\sigma_0+jw_0},A=\vert A \vert e^{\phi} \]
则
\[ \begin{aligned} x[n]&=\vert A \vert e^{\sigma_0} e^{(jw_0+\phi)} \\ &=\vert A \vert e^{\sigma_0}cos(jw_0+\phi)+j\vert A \vert e^{\sigma_0} sin(jw_0+\phi) \end{aligned} \]
得到序列\(x[n]\)的实部和虚部分别为
\[ x_{re}[n]=\vert A \vert e^{\sigma_0}cos(jw_0+\phi) \\ x_{im}[n]=\vert A \vert e^{\sigma_0} sin(jw_0+\phi) \]
若\(\alpha\)和\(A\)都是实数,则\(x[n]\)可简化为实指数序列。
矩形窗序列
矩形窗序列与称为\(box-car\)序列,该序列的特点是在有限范围内\(N_1 \leq n \leq N_2\)有单位样本值,在其他范围内为\(0\),如下:
\[ w_R[n]= \begin{cases} 1, \quad N_1 \leq n \leq N_2 \\ 0, \quad 其他 \end{cases} \]
如果一个矩形窗序列\(w_R[n]\)与一个序列\(x[n]\)相乘,则会提取出序列\(x[n]\)在\(N_1 \leq n \leq N_2\)内的样本值,即
\[ x[n] \cdot w_R[n]= \begin{cases} x[n], \quad N_1 \leq n \leq N_2 \\ 0, \quad 其他 \end{cases} \]
这个过程叫做加窗,在设计某些类型的数字滤波器有重要作用。
任意序列的表示
对于序列
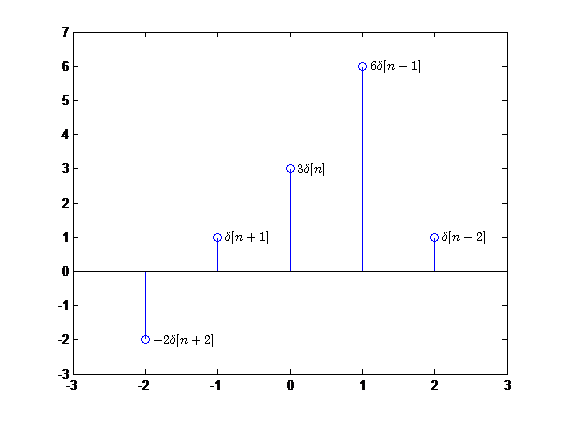
\[ x[n]=\{-2,1,\mathop{3}\limits_{\uparrow},6,1\} \]
可以表示为
\[ x[n]=-2\delta[n+2]+\delta[n+1]+3\delta[n]+6\delta[n-1]+\delta[n-2] \]
其实对于任何的序列都可以表示为单位冲激响应及其延迟的加权和。即
\[ x[n]=\sum_{m=-\infty}^{\infty}x[m]\delta [n-m] \]
想必大家已经看出来了
\[ \sum_{m=-\infty}^{\infty}x[m]\delta [n-m] \]
正是卷积\(x[n]*\delta[n]\),其实卷积运算的定义正是从此而来的,我们找到了将任意序列表达为单位冲激序列以及其延迟加权和的表达式,然后把这种表达式命名为一种的新的运算叫做卷积。
并且在这里我们得到一个重要的,关于卷积的公式,那就是
\[ x[n]=x[n]*\delta[n] \]
即,任何一个序列与单位冲激序列进行卷积后得到的序列是其本身,这是一个挺有用的结论,希望大家记住。
我们已经找到了任何序列的通用表达式,到这里大家想必隐隐约约对于卷积的重要性有点感觉了吧!
