当前位置：首页 > news >正文

网站建设的前期准备/谷歌浏览器下载安卓版

news 2025/8/2 14:27:37

网站建设的前期准备,谷歌浏览器下载安卓版,网站图片修改,创建全国文明城市工作要求没学过链式前向星或是邻接表就想做最短路径的题目？ Dijkstra太难懂？ 你的一切顾虑都可以被Floyd轻松消灭 --------------------------------------------------------------------------------------------------------------------------------- 前面…

没学过链式前向星或是邻接表就想做最短路径的题目？

Dijkstra太难懂？

你的一切顾虑都可以被Floyd轻松消灭

---------------------------------------------------------------------------------------------------------------------------------

前面所说的Dijkstra或是Bellman-ford,都有一个大前提，单源的最短路

也就是说，起点是一定的

但如果题目是计算u和v的最短路径，那就得做许多次单源最短路径的计算，时间太长了

而我们今天讲的Floyd是叫多源最短路径

也就是说，只需要调用一次这个函数，就可以把所有情况都涵盖到

思想：

利用动态规划的思想

f[i][j]表示i到j的最短路径

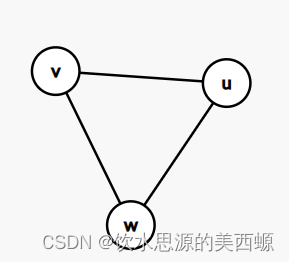
f[u][v]=min(f[v][w]+f[w][u],f[u][v])

代码：

void floyd(){for (int k=1;k<=n;k++){for (int i=1;i<=n;i++){for (int j=1;j<=n;j++){if (map[i][j]>map[i][k]+map[j][k]){map[i][j]=map[i][k]+map[j][k];}}}}
}

练习：

题目描述

平面上有n个点（n≤100），每个点的坐标均在-10000~10000之间。其中的一些点之间有连线。

若有连线，则表示可从一个点到达另一个点，即两点间有通路，通路的距离为两点间的直线距离。现在的任务是找出从一点到另一点之间的最短路径。

输入

共n+m+3行，其中:

第一行为整数n。

第2行到第n+1行（共n行），每行两个整数x和y，描述了一个点的坐标。

第n+2行为一个整数m(m<=1000)，表示图中连线的个数。

此后的m 行，每行描述一条连线，由两个整数i和j组成，表示第i个点和第j个点之间有连线(点编号从1开始)。

最后一行：两个整数s和t，分别表示源点和目标点。

输出

一行，一个实数（保留两位小数），表示从s到t的最短路径长度。

样例输入1

5
0 0
2 0
2 2
0 2
3 1
5
1 2
1 3
1 4
2 5
3 5
1 5

样例输出1

3.41

# include <iostream>
# include <cstdio>
# include <cstring> 
# include <cmath> 
using namespace std;
# define int long long
int n,m,s,t,m2;
struct node2{int x,y;
}a[105];
double map[105][105];
void floyd(){for (int k=1;k<=n;k++){for (int i=1;i<=n;i++){for (int j=1;j<=n;j++){if (map[i][j]>map[i][k]+map[j][k]){map[i][j]=map[i][k]+map[j][k];}}}}
}
signed main(){scanf("%lld",&n);for (int i=1;i<=n;i++){scanf("%lld%lld",&a[i].x,&a[i].y);	}scanf("%lld",&m);memset(map,0x7f,sizeof(map));for (int i=1;i<=m;i++){int u,v;scanf("%lld%lld",&u,&v);double w=sqrt((a[u].x-a[v].x)*(a[u].x-a[v].x)+(a[u].y-a[v].y)*(a[u].y-a[v].y));map[u][v]=map[v][u]=w;}scanf("%lld%lld",&s,&t);floyd(); printf("%.2lf",map[s][t]);return 0;
}