长春网站优化公司/百度推广手机app下载
SVM算法原理
SVM学习的基本想法是求解能够正确划分训练数据集并且几何间隔最大的分离超平面。如下图所示,
![]()
即为分离超平面,对于线性可分的数据集来说,这样的超平面有无穷多个(即感知机),但是几何间隔最大的分离超平面却是唯一的。
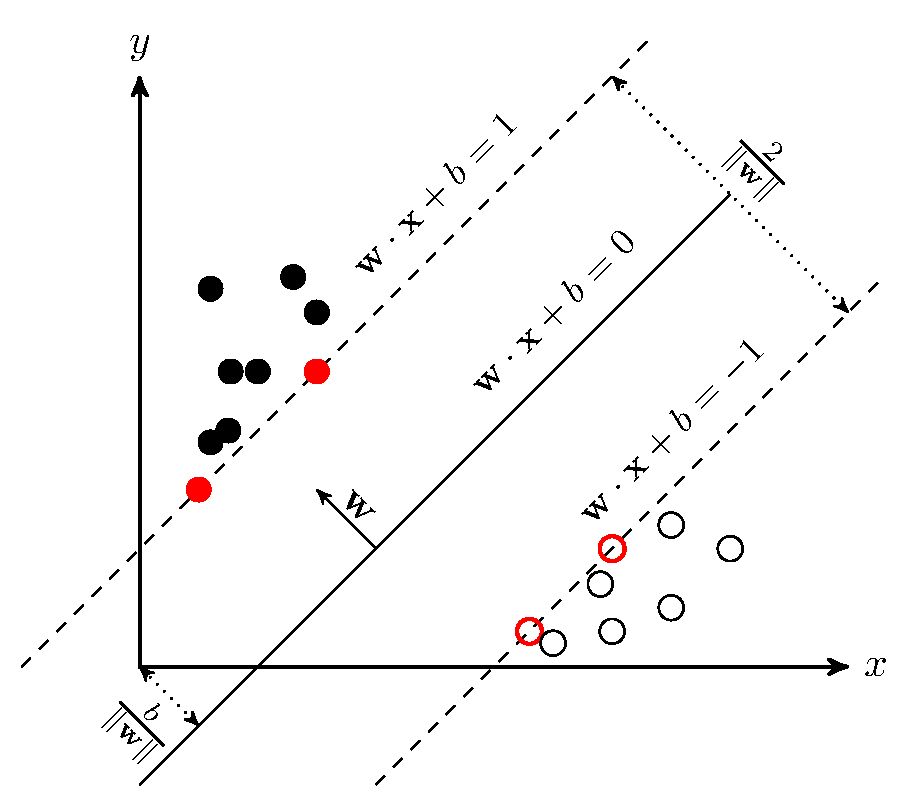
在推导之前,先给出一些定义。假设给定一个特征空间上的训练数据集

几何间隔:对于给定的数据集T和超平面![]() ,定义超平面关于样本点 的几何间隔为
,定义超平面关于样本点 的几何间隔为![]()
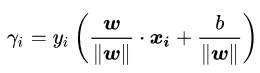
*在支持向量机中,当样本点被超平面正确分类时,该点与超平面的距离被定义为几何间隔。
超平面关于所有样本点的几何间隔的最小值为![]()
实际上这个距离就是我们所谓的支持向量到超平面的距离。
根据以上定义,SVM模型的求解最大分割超平面问题可以表示为以下约束最优化问题![]()
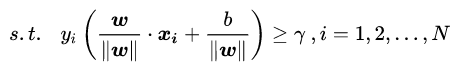
也就是找出最大的最小值。
简化:将约束条件两边同时除以 γ ,得到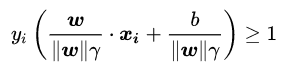 。
。
因为 ![]() 都是标量,所以为了表达式简洁起见,令
都是标量,所以为了表达式简洁起见,令 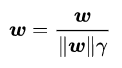
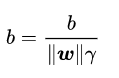 得到
得到 ![]() 。
。
又因为最大化 γ ,等价于最大化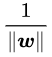 ,(毕竟分母变大了,为了整体不变)也就等价于最小化
,(毕竟分母变大了,为了整体不变)也就等价于最小化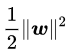 (
(![]() )是为了后面求导以后形式简洁,不影响结果),因此SVM模型的求解最大分割超平面问题又可以表示为以下约束最优化问题
)是为了后面求导以后形式简洁,不影响结果),因此SVM模型的求解最大分割超平面问题又可以表示为以下约束最优化问题
![]()
![]()
变换历程有:
有 ![]() ,
,![]() =》得
=》得![]() =》求
=》求 ![]() =》求
=》求![]() =》得
=》得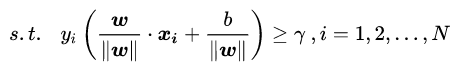 =》化简
=》化简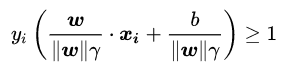
=》换元![]() =》最大化 γ =》求得
=》最大化 γ =》求得![]()
这是一个含有不等式约束的凸二次规划问题,可以对其使用拉格朗日乘子法得到其对偶问题。
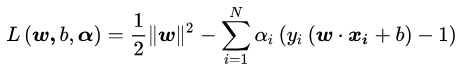
其中αi为拉格朗日乘子,且αi>=0。现在我们令
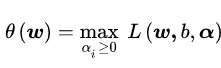
于是原约束问题就等价于:
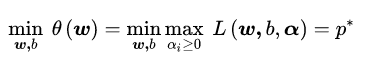
看一下我们的新目标函数,先求最大值,再求最小值。这样的话,我们首先就要面对带有需要求解的参数 ω 和 b 的方程,而αi又是不等式约束,这个求解过程不好做。所以,我们需要使用拉格朗日函数对偶性,将最小和最大的位置交换一下,这样就变成了:
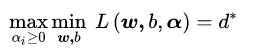
把目标式子加一个负号,将求解极大转换为求解极小

最后经过转换因此可以得到:
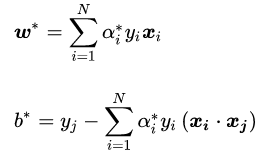
结论:

关于松弛:
到这里都是基于训练集数据线性可分的假设下进行的,但是实际情况下几乎不存在完全线性可分的数据,为了解决这个问题,引入了“软间隔”的概念,即允许某些点不满足约束
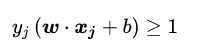
采用hinge损失,将原优化问题改写为
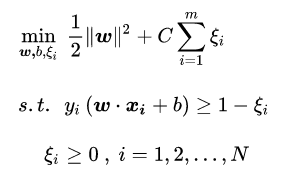
ξ的范围为: 0 到 1超出的部分

综合以上讨论,我们可以得到线性支持向量机学习算法如下:


例题:

