什么是中国剩余定理呢？

 当m1,m2,....mn的值两两互质的时候，求x的值。

假设 M = m1 * m2 * ... * mn

在设 Hi = M / mi （也就是除了mi之外，其他的m值的乘积）

由于m1,m2...mn两两互质， 所以Hi与mi是互质的。

那么Hi ^ (-1)  也就是 Hi 关于 mod mi 的逆元是存在的。

（使用扩展欧几里得算法进行求解这个逆元，因为当下只有Hi,与mi互质这一个条件

也就是  Hi * (Hi ^ -1)  + y * mi = 1  使用扩展欧几里得算法将x求出，也就是Hi ^ -1）

则： x = a1 * H1 * ( H1 ^ -1) + a2 * H2 * (H2 ^ -1) + ... + ak * Hk * (Hk ^ -1).  （这个就是中国剩余定理的一个通用公式，但是应用的前提条件是,m1,m2,m3...两两互质。）

以第一个方程 mod m1为例：

H1 * H ^( -1) mod m1 == 1 , 而其他的H2,H3....中都包含了m1,所以mod m1为0.

所以 x = a1 * a mod m1 . 成立。

那么问题来了：

如果m1,m2,m3...不两两互质呢。那就要用到数学归纳法的思想，将两两方程不断合并，最后就变为了一个方程了。

还是这些方程，但是现在没有m1,m2...两两互质。该怎么办呢？

先取出前面两个方程出来。并换一种表现形式

x == k1 * m1 + a1 

x == k2 * m2 + a2

那么也就是说明了

k1 * m1 + a1 == k2 * m2 + a2

--->k1 * m1 - k2 * m2 == a2 - a1

这就可以用扩展欧几里得的方式求解出一组k1,k2出来。

但是要存在有解 则 (a2 - a1) 能够整除 gcd(m1,m2);

 所以真正的k1就是 k1 =k1 *  (a2 - a1) / gcd(m1,m2);

而k1的通解是, k1 + k * (m2 / gcd(m1,m2));

则将k1的通解带入到方程中，就可以得到一个新的关于x的方程

x == ( k1 + k * (m2 / gcd(m1,m2))  ) * m1 + a1;

x == k1 * m1 + a1  + k * m1 * m2 / gcd(m1,m2);

x == k1 * m1 + a1 + k * lcm【m1,m2】 (lcm【m1,m2】为m1,m2的最小公倍数)

而k1 * m1 + a1 就是 新的 a1(而这个k1 * m1 + a1不就是我们每次以第一个公式作为合并基准的公式嘛) ,  而 lcm【m1,m2】就是新的m1 

而这个x 就是前两个方程合并 后 得到的一个新的方程。

同样，新的方程 和 第三个方程合并又可以将两个方程变为一个方程，以此类推，直到最后只剩下一个方程。

这个m1，m2,a1，k1已经在合并过程中不断发生了变化。

x == k1 * m1 + a1 + k * lcm【m1,m2】

得到的最后一个这个公式的m1和a1

实际上就是 x mod m1 == a1的含义了。

而我们要求出这个最后一个公式的其中一个满足条件的x.

所以取 x = ( a1 % m1 + m1) % m1即可。 

题目链接：https://www.acwing.com/problem/content/206/

题目：

给定 2n个整数 a1,a2,…,an 和 m1,m2,…,mn，求一个最小的非负整数 x，满足 ∀i∈[1,n],x≡mi(mod ai)。

输入格式

第 1 行包含整数 n。

第 2…n+1 行：每 i+1 行包含两个整数 ai和 mi，数之间用空格隔开。

输出格式

输出最小非负整数 x，如果 x不存在，则输出 −1。
如果存在 x，则数据保证 x 一定在 64 位整数范围内。

数据范围

1≤ai≤2e31 - 1,
0≤mi<ai
1≤n≤25

输入样例：

2
8 7
11 9

输出样例：

31

分析：

按照上面m1,m2,m3...不一定互质的分析来就可以了。

但是要注意，此题是 

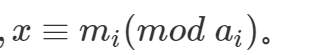
不要和上面的m和a混淆了。 

最后此题会变为：

x == k1 * a1 + m1 + k * lcm[a1,a2]

新的m1 为 k1 * a1 + m1

新的a1为 lcm[a1.a2];

代码实现：

# include <iostream>
using namespace std;int n;long long exgcd(long long a ,long long b , long long & x , long long & y)
{if(!b){x = 1 , y = 0;return a;}else{int t = exgcd(b,a % b , y , x);y -= a / b * x;return t;}
}int main()
{scanf("%d",&n);bool flag = true;long long a1,m1,a2,m2;scanf("%lld %lld",&a1,&m1); // 先存入第一个方程，我们的合并是通过两个两个不断和并为1个最后化为一个方程for(int i = 2 ; i <= n ; i++){scanf("%lld %lld",&a2,&m2);long long k1,k2;long long t = exgcd(a1,a2,k1,k2);if((m2 - m1) % t)  // 无解{flag = false;break;}else{k1 = (m2 - m1) / t * k1; //真正的k1,k2k2 = (m2 - m1) / t * k2; // 而k2实际上用不到k1 = ( k1 % (a2 / t) + a2 / t ) % (a2 / t); // 最小的正整数k1, 为了防止其爆long long,k1尽量取小m1 = k1 * a1 + m1;a1 =  a1 / t * a2; // 新的a1为 a1,a2的最小公倍数}}if(flag){printf("%lld\n",(m1 % a1 + a1) % a1);}else{printf("-1\n");}return 0;
}