写在之前
李超线段树 简称\(LCT\)
正式开始
李超线段树主要用于维护这样一类问题
有两个操作
1.插入一条直线(k,b) \(y=kx+b\)
2.给出一个值\(x\) 求\(x=k\)与这些直线交点中纵坐标的最大值
我们可以使用\(CDQ\)分治或者平衡树维护
但是这里有了一种玄学鬼畜的数据结构 李超线段树
\(TA\)的形状同正常的线段树
但是维护的是区间内的优势线段 也就是覆盖最多的线段
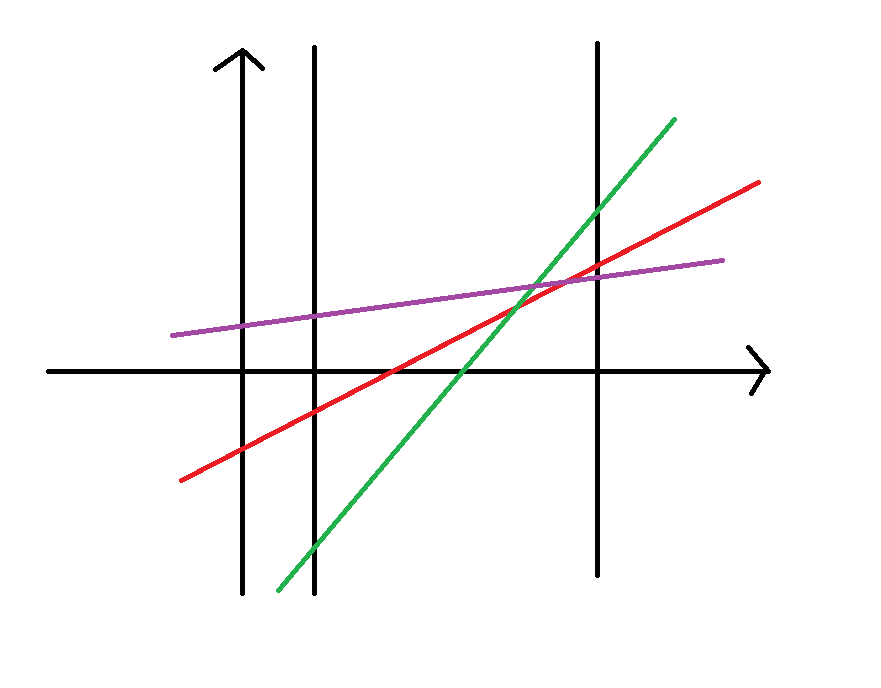
比如说 该区间内覆盖最多的线段就是紫色线段
考虑怎么维护
首先对于当前区间\([le,ri]\)
我们假设已经维护了一条最优线段\(old\)
现在加入一条线段\(new\)
存在四种情况
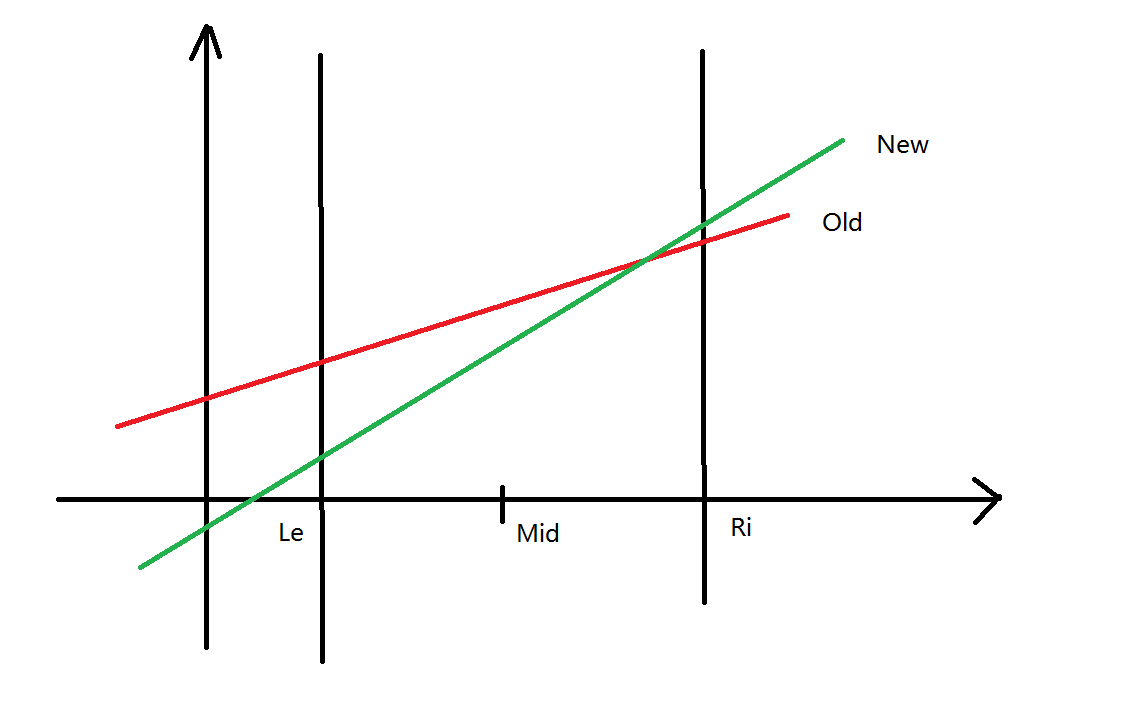
1.\(k_{new}>k_{old}\)
并且\(x=mid\)时 \(y_{old}>y_{new}\) 这个时候
优势线段依然是\(old\)左区间同样 但是右区间不一定
所以我们使用\(new\)去更新右区间 \((mid,ri]\)
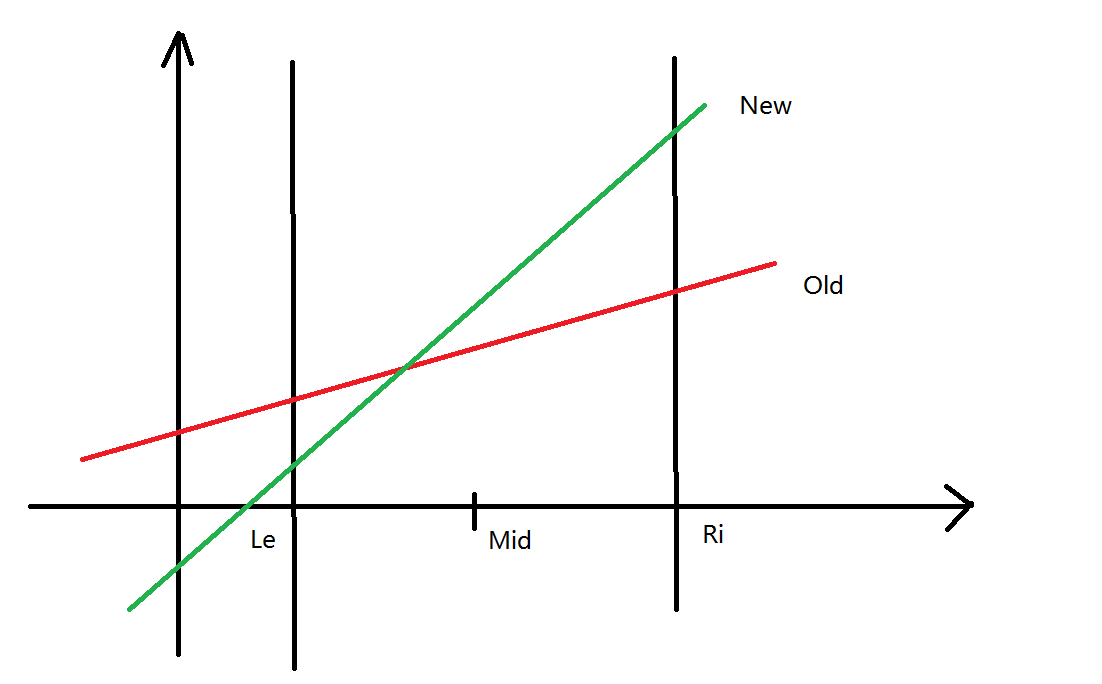
2.\(k_{new}>k_{old}\)
并且\(x=mid\)时 \(y_{old}<y_{new}\) 这个时候
优势线段更新为\(new\) 右区间同样是
但是左区间不一定
所以我们再使用\(old\)去更新左区间\([le,mid]\)
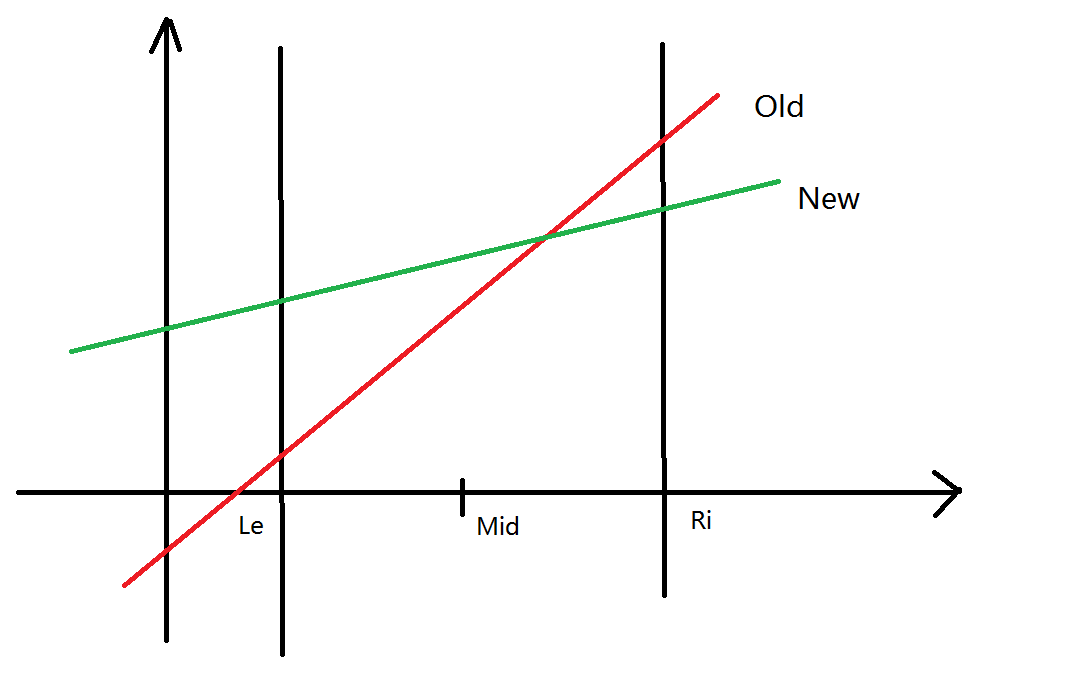
3.\(k_{new}<k_{old}\)
并且\(x=mid\)时 \(y_{old}<y_{new}\) 这个时候
优势线段更新为\(new\) 左区间同样是
但是右区间不一定
所以我们再使用\(old\)去更新左区间\((mid,ri]\)
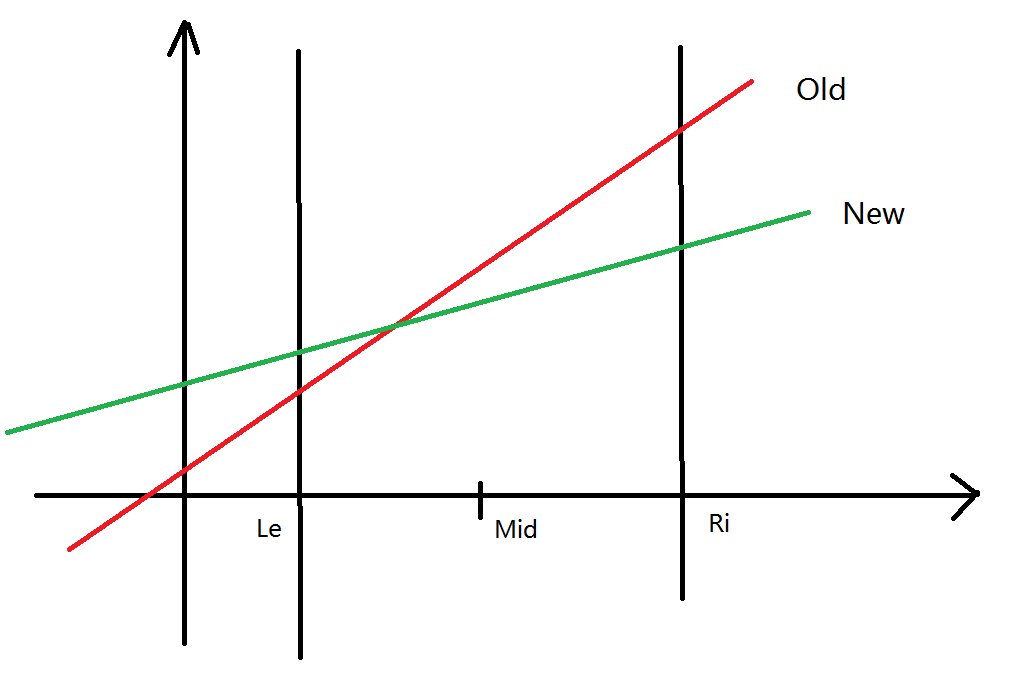
4.\(k_{new}<k_{old}\)
并且\(x=mid\)时 \(y_{old}>y_{new}\) 这个时候
优势线段依然是\(old\) 右区间同样是
但是左区间不一定
所以我们使用\(new\)去更新左区间\([le,mid]\)
这就是维护
至于查询的
我们使用到了标记永久化的思想
从上到下 不断比较 逐个取\(max\)
例题
P4254 [JSOI2008]Blue Mary开公司
这是一道板子题
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<cstdlib>
#include<string>
#include<queue>
#include<map>
#include<stack>
#include<list>
#include<set>
#include<deque>
#include<vector>
#include<ctime>
#define ll long long
#define inf 0x7fffffff
#define maxn 50005
#define IL inline
#define M 1008611
#define D double
#define mod 998244353
#define R register
using namespace std;
template<typename T>IL void read(T &_)
{T __=0,___=1;char ____=getchar();while(!isdigit(____)) {if(____=='-') ___=0;____=getchar();}while(isdigit(____)) {__=(__<<1)+(__<<3)+____-'0';____=getchar();}_=___ ? __:-__;
}
/*-------------OI使我快乐-------------*/
int n,ans,cnt,tot;
int tre[M<<2];
D cdy[M],wzy[M];
char key[20];
IL D have(int id,int x){return cdy[id]*(x-1)+wzy[id];}
IL void update(int si,int le,int ri,int id)
{if(have(id,le)>have(tre[si],le)&&have(id,ri)>have(tre[si],ri)) {tre[si]=id;return;}if(have(id,le)<=have(tre[si],le)&&have(id,ri)<=have(tre[si],ri)) return;int mid=(le+ri)>>1;if(cdy[tre[si]]<cdy[id]){if(have(id,mid)>have(tre[si],mid)) {update(si<<1,le,mid,tre[si]);tre[si]=id;}else update(si<<1|1,mid+1,ri,id);}else{if(have(id,mid)>have(tre[si],mid)) {update(si<<1|1,mid+1,ri,tre[si]);tre[si]=id;}else update(si<<1,le,mid,id);}
}
IL D qury(int si,int le,int ri,int pos)
{if(le==ri) return have(tre[si],pos);int mid=(le+ri)>>1;if(pos<=mid) return max(have(tre[si],pos),qury(si<<1,le,mid,pos));else return max(have(tre[si],pos),qury(si<<1|1,mid+1,ri,pos));
}
int main()
{
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);read(n);while(n--){int x;scanf("%s",key+1);if(key[1]=='P'){++tot;scanf("%lf%lf",&wzy[tot],&cdy[tot]);update(1,1,maxn,tot);}else{read(x);printf("%d\n",(int)(qury(1,1,maxn,x)/100.0));}}
// fclose(stdin);
// fclose(stdout);return 0;
}P4655 [CEOI2017]Building Bridges
首先这是一道\(dp\)
\[sum[i]=\sum_{i=1}^n w_i\]
\[dp[i]=min\{dp[j]+sum[i-1]-sum[j]+(h[i]-h[j])^2\}(1≤j<i)\]
最终的答案就是\(dp[n]\)
拆开之后就是
\(dp[i]=min\{dp[j]+sum[i-1]-sum[j]+h[i]^2-2* h[i]* h[j]+h[j]^2\}\)
那么就是查询\(x=h[i]\)时
线段\(y=kx+b\)
\[k=-2* h[j]\]
\[b=h[j]^2-sum[j]+dp[j]\]
对应的\(y\)的最小值 所以我们可以直接使用李超线段树维护
由于定义域为\([-10^6,10^6]\) 李超线段树又是类似于权值线段树
所以我们需要维护成\([0,2* 10^6]\)
然后就是基本操作了
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<cstdlib>
#include<string>
#include<queue>
#include<map>
#include<stack>
#include<list>
#include<set>
#include<deque>
#include<vector>
#include<ctime>
#define ll long long
#define inf 1e12
#define N 100008
#define IL inline
#define M 1000611
#define D double
#define maxn 2000008
#define R register
using namespace std;
template<typename T>IL void read(T &_)
{T __=0,___=1;char ____=getchar();while(!isdigit(____)) {if(____=='-') ___=0;____=getchar();}while(isdigit(____)) {__=(__<<1)+(__<<3)+____-'0';____=getchar();}_=___ ? __:-__;
}
/*-------------OI使我快乐-------------*/
ll n;
ll num[N],hei[N];
ll sum[N],dp[N];
ll cdy[N],wzy[N],tre[M*20];
IL ll have(ll id,ll x){return cdy[id]*(x-1000000)+wzy[id];}
IL void update(ll si,ll le,ll ri,ll id)
{if(have(id,le)<have(tre[si],le)&&have(id,ri)<have(tre[si],ri)) {tre[si]=id;return;}if(have(id,le)>=have(tre[si],le)&&have(id,ri)>=have(tre[si],ri)) return;ll mid=(le+ri)>>1;if(cdy[tre[si]]<cdy[id]){if(have(id,mid)<have(tre[si],mid)) {update(si<<1|1,mid+1,ri,tre[si]);tre[si]=id;}else update(si<<1,le,mid,id);}else {if(have(id,mid)<have(tre[si],mid)) {update(si<<1,le,mid,tre[si]);tre[si]=id;}else update(si<<1|1,mid+1,ri,id);}
}
IL ll qury(ll si,ll le,ll ri,ll pos)
{
// printf("%lld %lld %lld %lld\n",si,le,ri,pos);
// printf("noat %lld\n",tre[si]);if(le==ri) return have(tre[si],pos);
// puts("now at at");ll mid=(le+ri)>>1;
// printf("now at %lld\n",mid);if(pos<=mid) return min(have(tre[si],pos),qury(si<<1,le,mid,pos));else return min(have(tre[si],pos),qury(si<<1|1,mid+1,ri,pos));
}
int main()
{
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);read(n);for(R ll i=1;i<=n;++i) read(hei[i]);for(R ll i=1;i<=n;++i) read(num[i]);for(R ll i=1;i<=n;++i) sum[i]=sum[i-1]+num[i];cdy[0]=wzy[0]=inf;cdy[1]=-2*hei[1];wzy[1]=hei[1]*hei[1]-num[1];update(1,0,maxn,1);for(R ll i=2;i<=n;++i){
// printf("now at %lld\n",i);ll tmp=qury(1,0,maxn,hei[i]+1000000);
// puts("now at at at at at at at at at at at at at at at at ");dp[i]=tmp+sum[i-1]+hei[i]*hei[i];cdy[i]=-2*hei[i];wzy[i]=dp[i]+hei[i]*hei[i]-sum[i];update(1,1,maxn,i);}printf("%lld\n",dp[n]);
// fclose(stdin);
// fclose(stdout);return 0;
}P4097 [HEOI2013]Segment
这题不一样 维护的是线段
首先对于区间\([le,ri]\)
只有当\(le=x_0\&\&x_1=ri\)时才可以产生贡献
然后对于\(x_0=x_1\)时 由于不存在斜率 需要特判
由于输出编号 所以我维护的是\(pair<>\)
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<cstdlib>
#include<string>
#include<queue>
#include<map>
#include<stack>
#include<list>
#include<set>
#include<deque>
#include<vector>
#include<ctime>
#define ll long long
#define inf 1e15
#define N 500008
#define IL inline
#define M 1008611
#define D double
#define eps 1e-5
#define maxn 40000
#define R register
using namespace std;
template<typename T>IL void read(T &_)
{T __=0,___=1;char ____=getchar();while(!isdigit(____)) {if(____=='-') ___=0;____=getchar();}while(isdigit(____)) {__=(__<<1)+(__<<3)+____-'0';____=getchar();}_=___ ? __:-__;
}
/*-------------OI使我快乐-------------*/
struct Node
{D kx,bx;
}e[N];
int n,tot,ans;
int tre[M];
pair<D,int> fro[M];
IL D key(int at,int now){return e[now].kx*((D)at)+e[now].bx;}
IL void update(int si,int lenow,int rinow,int le,int ri,int id)
{if(le==lenow&&rinow==ri){if(key(le,id)>key(le,tre[si])&&key(ri,id)>key(ri,tre[si])) {tre[si]=id;return;}if(key(le,id)<=key(le,tre[si])&&key(ri,id)<=key(ri,tre[si])) return;int mid=(lenow+rinow)>>1;if(e[id].kx>=e[tre[si]].kx){if(key(mid,id)>=key(mid,tre[si])) update(si<<1,lenow,mid,le,mid,tre[si]),tre[si]=id;else update(si<<1|1,mid+1,rinow,mid+1,ri,id);}else{if(key(mid,id)>=key(mid,tre[si])) update(si<<1|1,mid+1,rinow,mid+1,ri,tre[si]),tre[si]=id;else update(si<<1,lenow,mid,le,mid,id);}}int mid=(lenow+rinow)>>1;if(ri<=mid) update(si<<1,lenow,mid,le,ri,id);else if(mid<le) update(si<<1|1,mid+1,rinow,le,ri,id);else update(si<<1,lenow,mid,le,mid,id),update(si<<1|1,mid+1,rinow,mid+1,ri,id);
}
IL pair<D,int> comp(pair<D,int> cdy,pair<D,int> wzy)
{if(fabs(cdy.first-wzy.first)<eps) {if(cdy.second>wzy.second) return wzy;else return cdy;}else{if(cdy.first>wzy.first) return cdy;else return wzy;}
}
IL pair<D,int> qury(int si,int le,int ri,int pos)
{if(le==ri) return make_pair(key(le,tre[si]),tre[si]);int mid=(le+ri)>>1;if(pos<=mid) return comp(make_pair(key(pos,tre[si]),tre[si]),qury(si<<1,le,mid,pos));else return comp(make_pair(key(pos,tre[si]),tre[si]),qury(si<<1|1,mid+1,ri,pos));
}
int main()
{freopen("lct.in","r",stdin);freopen("lct.out","w",stdout);read(n);for(R int i=1;i<=maxn;++i) fro[i].first=-inf,fro[i].second=0;e[0].bx=-inf;while(n--){int knd;read(knd);if(knd==1){int ax,ay,bx,by;read(ax);read(ay);read(bx);read(by);ax=(ax+ans)%39989+1;ay=(ay+ans)%1000000000+1;bx=(bx+ans)%39989+1;by=(by+ans)%1000000000+1;++tot;if(ax==bx){
// puts("cdy cdy");if(ay<by) swap(ay,by);if(fro[ax].first<ay) fro[ax].first=ay,fro[ax].second=tot;}else{
// puts("wzy wzy");if(ax>bx) swap(ax,bx),swap(ay,by);
// printf("(%d , %d) (%d , %d)\n",ax,ay,bx,by);e[tot]=(Node){((D)(by-ay))/((D)(bx-ax)),by-bx*((D)(by-ay))/((D)(bx-ax))};update(1,1,maxn,ax,bx,tot);}}else{int x;read(x);x=(x+ans)%39989+1;pair<D,int> tmp=qury(1,1,maxn,x);if(tmp.first==-inf&&fro[x].first==-inf) ans=0,puts("0");else{if(fabs(tmp.first-fro[x].first)<eps) {if(tmp.second<fro[x].second) printf("%d\n",ans=tmp.second);else printf("%d\n",ans=fro[x].second);}else{if(tmp.first>fro[x].first) printf("%d\n",ans=tmp.second);else printf("%d\n",ans=fro[x].second); }}}}fclose(stdin);fclose(stdout);return 0;
}\(leige\) :省选考这玩意我当场吃**
