资讯门户类网站/百度网页制作

plot3(x1,y1,z 1,.'b )';

plot3(x2,y2,z 2,.'b )';

创建交互式界面部分:创建界面图形,利用静态文本框添加提示文本信息,再利用编辑文本框输入相应参数并调用绘图文件。

图2为输入参数后的双点光源干涉图,其中两光源取在x 轴上关于原点对称相距为2mm ,波长K =

63218nm ,平面为-x -10g+1000=0,观察窗口宽度为20@20mm 2可以看出平面中间部分为等间距干

涉条纹,两边为弧形条纹;若取平面x =250mm 时得到一组同心圆条纹。如果改变输入参数即任意改变平面的位置,及改变观察窗口的位置和大小,将得到三维空间任意位置的干涉图。

若考虑双点光源发射的是球面光波,光场各处的光强随着传播距离增大而变小,则可以通过公式

(3)计算平面上各点光强。其中I W 1/r 2,假设振幅为1,则程序中光强计算式为

I =1r 21+1r 22+2r 1r 2

cos D (5)假设两光源位于x 轴关于原点对称相距为014mm ,波长K =0106mm ,则在y =-6mm 的平面得到如图3所示干涉图样。

从图3可以看出平面上距离光源最近处(即平面中心)干涉条纹最亮,随着平面上的位置到光源的距离的增大干涉条纹逐渐变暗,即光强变弱。如果以所选取的平面为xy 平面,以平面上各个点的光强为该点的z 轴坐标,则可以绘出如图4所示干涉条纹光强度的变化图,该图很好的反映了平面上各点

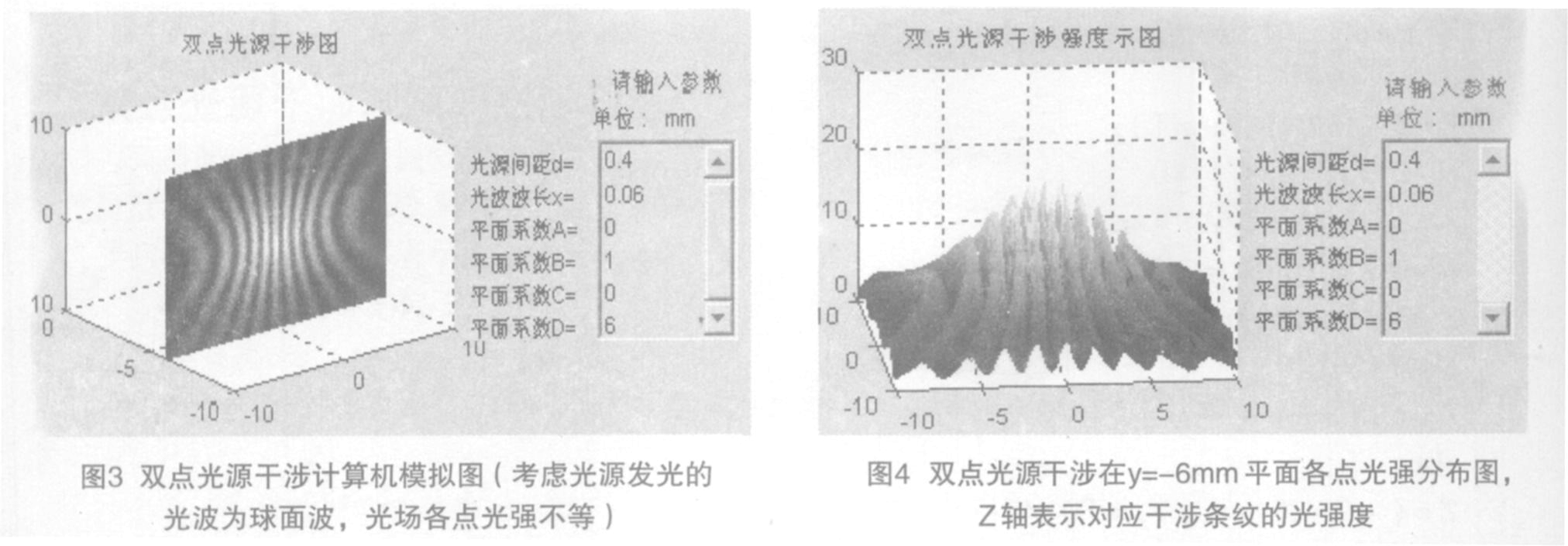
光强度的变化情况。

在模拟过程中可以看到,干涉条纹间距随着平面被观察位置到光源的距离的增大而增大、随着波长的增大而增大、随着点光源之间距离的增大而减小。当平面到光源的距离过小时,出现干涉条纹模糊不清(亦即肉眼所不能分辨),若放大观察窗口的尺寸比例,干涉条纹将又变得清晰。特别地,当观察位置包括点光源时,由于观察面上光强度对比太大,所以只能看到光源点。模拟的结果很好的反应了双点光源干涉特性。

4 结束语

本文从数学模型出发,利用MATL AB 语言模拟双点光源的干涉现象,并且建立交互式界面,可以方便的通过改变输入参数来观察在不同条件下(不同平面、不同光波波长、不同的点光源间距)三维空间任意平面的干涉条纹及其光强度分布,这弥补了实验的不足,给实验教学带来了便利。

参考文献:

[1]宋清,熊万杰.光学现象的计算机模拟[J].中山大学学报论丛,2005,25(3):24-30.

[2]梁齐,许晓琳,王明虎.光干涉现象的计算机模拟[J].大学物理实验,2003,16(3):61-63.

[3]姚启钧.光学教程[M ].北京:高等教育出版社,1995.

[4]羊国光,宋菲君.高等物理光学[M ].合肥:中国科学技术大学出版社,1991.

[5]尹泽明,丁春利.精通MATLAB6[M ].北京:清华大学出版社,2002.

#48#贵州大学学报(自然科学版)第24卷