用python实现PID控制器 (PyCharm)

PID框图

PID 的控制框图如下图所示：

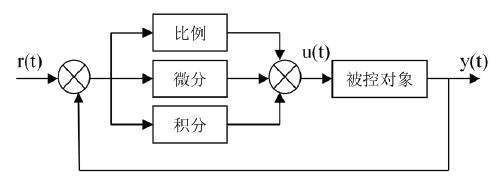
python实现

控制器

PID的三个参数一般是我们自己设计的，而且一般是固定的，所以最好在初始化的时候设置一下。

在具体实现的时候，当前误差需要知道系统的输出和目标值，因此误差作为参数传入。dt是系统的步长，即调节周期，也将其作为参数传入

为了适应某些变参数算法（al，bp），设计一个函数仅用来改变三个参数

控制器代码如下：

class PID_Controller:# 给pid的三个参数赋初值def __init__(self, kp, ki, kd):self.kp = kpself.ki = kiself.kd = kdself.last_error = 0.0self.integral = 0.0def change_para(self, kp, ki, kd):self.kp = kpself.ki = kiself.kd = kddef control_action(self, error, dt):"""Args:error: 当前误差dt: 步长Returns: pid的输出"""p = self.kp * errorself.integral += errori = self.ki * self.integralderivative = (error - self.last_error) / dtd = self.kd * derivativeself.last_error = errorreturn p + i + d

被控对象

被控对象一般是用传递函数表示的，这边可以用欧拉公式实现

对传递函数为：

$$G(S)=\frac{3.1877}{S^2+4900}$$

进行变换

import numpy as npclass levitationSys:def __init__(self, ncount, x10, x20, y10, y20):self.x10 = x10self.x20 = x20self.X1 = np.zeros(ncount)self.y10 = y10self.y20 = y20self.Y1 = np.zeros(ncount)self.Y2 = np.zeros(ncount)def system_io(self, i, input, h, f):y1 = self.y10 + h * self.y20y2 = self.y20 + h * (-4900 * self.y10 + 3.1877 * input);self.Y1[i] = self.y10self.Y2[i] = self.y20self.y10 = y1self.y20 = y2return y1

主函数

控制器和传递函数设计好之后，我们只需要建立一个主函数去调用它即可

from pid import PID_Controller
from system import levitationSysimport matplotlib.pyplot as plt
import numpy as npif __name__ == '__main__':wc = 50kp = wc * wc / 3.2ki = 15kd = wc / 1.6ncount = 200000    # 循环次数h = 0.0002  #步长ts = np.zeros(ncount)# 被控对象sys = levitationSys(ncount, 0, 0, 0, 0)# 控制器PID = PID_Controller(kp, ki, kd)gap = 0.0gap_last = 0.0for i in range(ncount):gap = sys.system_io(i, PID.control_action(0.004 - gap_last, h), h, 0)ts[i] = i * hprint(gap)gap_last = gap# 图像输出plt.plot(ts, sys.Y1)plt.xlabel('x-axis')plt.ylabel('y-axis')plt.title('Simple Line Plot')plt.show()

运行结果:

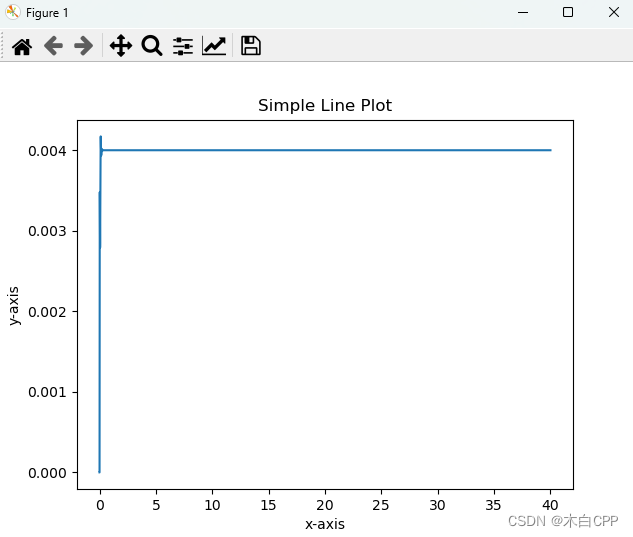
调参顺序建议

1. 先调节比例系数 kp，使系统的响应能够快速达到稳定状态，并具有合理的超调量。因为它是最基本的参数，可以快速反应出控制效果。
2. 然后调节积分时间常数 ki，使系统的静态误差消失或达到最小值。增加 ki 可以减小稳态误差，但过大的 ki 会引起系统的震荡和不稳定。
3. 调节微分时间常数 kd，使系统的稳定性和动态响应之间取得平衡。增加 kd 可以使系统更加稳定,减小系统的超调和振荡,但过大的 kd 会引起系统的噪声和抖动。
4. 最后综合进行微调

需要注意的是，这只是一种基本的调参顺序，实际情况可能因为不同系统的特点而有所不同

程序下载

https://mp.csdn.net/mp_download/manage/download/UpDetailed