鄂尔多斯网站制作/盐城网站优化
记忆
函数可以利用对象去记住先前操作的结果,从而能避免无谓的运算。这种优化被称为记忆。JavaScript的对象和数组要实现这种优化是非常方便的。
使用递归函数计算fibonacci数列。
var fibonacci=function(n){return n<2?n:fibonacci(n-1)+fibonacci(n-2);
};
for(var i=0;i<=10;i+=1){document.write("<br/>"+i+';'+fibonacci(i));
}
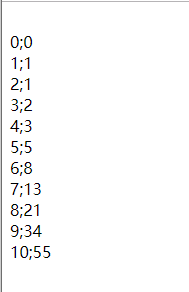
使用临时变量保存存储结构,存储结果隐藏在闭包中。
var fibonacci=(function(){var memo=[0,1];var fib=function(n){var result=memo[n];if(typeof result !=='number'){result=fib(n-1)+fib(n-2);memo[n]=result;}return result;};return fib;
}());
for(var i=0;i<=10;i+=1){document.write('<br/>'+i+';'+fibonacci(i));
}

构建模块
使用函数和闭包可以构建模块。所谓模块,就是一个提供接口却隐藏状态与实现的函数或对象。通过使用函数构建模块,可以完全摒弃全局变量的使用,从而规避JavaScript语言缺陷。全局变量是JavaScript最为糟糕的特征之一,在一个大中型web应用中,全局变量简直就是一个魔鬼,会带来无穷的灾难。
var serial_marker=function(){var prefix='';var seq=0;return {set_prefix:function(p){prefix=String(p);},set_seq:function(s){seq=s;},gensym:function(){var result=prefix+seq;seq+=1;return result;}};
};
var seqer=serial_marker();
seqer.set_prefix('Q');
seqer.set_seq(1000);
var unique=seqer.gensym();
document.write(unique);
document.write("<br/>");
var unique=seqer.gensym();
document.write(unique);

柯里化
柯里化是把接收多个参数的函数变换成接收一个单一参数的函数,并且返回一个新函数,这个新函数能够接收原函数的参数。
function adder(num){return function(x){return num+x;}
}
var add5=adder(5);
var add6=adder(6);
document.write(add5(1));
document.write("<br/>")
document.write(add6(5));

函数柯里化的主要功能是提供强大的动态函数创建支持。通过调用另一个函数并为它传入要柯里化(currying)的函数和必要的参数,通俗地说就是利用已有的函数,再创建一个动态函数,该动态函数内部还是通过已有的函数来发生作用,只是传入更多的参数来简化函数的参数方面的调用。
函数柯里化的基本方法和函数绑定是一样的;使用一个闭包返回一个函数。
创建柯里化函数的通用方式:
function curry(fn){var args=Array.prototype.slice.call(arguments,1);return function(){var innerArgs=Array.prototype.slice.call(arguments);var finalArgs=args.concat(innerArgs);return fn.apply(null,finalArgs);};
}
高阶函数
高阶函数作为函数编程众多风格中的一项显著特征,经常被使用。实际上,高阶函数是对函数的进一步抽象。
高阶函数至少满足下列条件之一:
- 接收函数作为输入。
- 输出一个函数。
在函数式语言中,函数不但是一种特殊的对象,还是一种类型,因此函数本身是一个可以传来传去的值。也就是说,某个一个函数在刚开始执行的时候,可以送入一个函数的参数。传入的参数本身就是一个函数。当然,这个输入的函数相当于某一个函数的另外一个函数。当函数执行完毕之后,又可以返回另外一个新的函数,这个返回函数取决于return fn(){……}。
例子-函数作为参数
alert([2,6,4,9,0,2,5].sort());

高阶函数
function map(array,func){var res=[];for(var i=0,len=array.length;i<len;i++){res.push(func(array[i]));}return res;
}
var mapped=map([1,3,5,7,8],function(n){return n=n+1;
});
document.write(mapped);
var mapped2=map(["one","two","three","four"],function(item){return "("+item+")";
});
document.write("<br/>");
document.write(mapped2);

递归算法
递归是函数对自身的调用。任何一个有意义的递归总是由两部分组成的:递归调用和递归终止条件,递归运算在无限制的情况下,会无休止地自身调用。。显然,程序不应该出现这种无休止的递归调用,只应出现有限次数、有终止的调用。为此,一般递归运算中要结合if语句来进行控制。只有在某条件成立才可以继续执行递归调用,否则就不再继续。
问题的定义是递归的
数学上常用阶乘函数、幂函数和斐波那契数列。
var f=function(x){if(x<2){return 1;}else{return x*arguments.callee(x-1);}
}
alert(f(5));

问题所涉及的数据结构是递归的
问题本身虽然不是递归定义的,但是它所用到的数据结构是递归的。
function f(n){var a=1;if(n.nodeType==1){a++;}var child=n.childNodes;for(var i=0;i<child.length;i++){i+=f(child[i]);}return 1;
}
window.onload=function(){var body=document.getElementsByTagName("body")[0];alert(f(body));
}

问题的解决满足递归的特性
Hanoi(汉诺)塔问题
function f(n,a,b,c){if(n==1){document.write(a+"→"+c+"<br/>");}else{f(n-1,a,c,b);document.write(a+"→"+c+"<br/>");f(n-1,b,a,c);}
}
f(3,"A","B","C");

尾递归算法
尾递归是针对传统递归算法的一种优化算法,它是从最后开始计算,每递归一次就是出相应的结果。也就是说,函数调用出现在调用函数的尾部,因为是尾部,所以就不用去保存任何局部变量,返回时调用函数就可以直接越过调用者,返回调用者的调用者。
阶乘的一种普通线性递归运算。
function f(n){return (n==1)?1:n*f(n-1);
}
alert(f(5));

尾递归算法
function f(n){return (n==1)?1:e(n,1);
}
function e(n,a){return (n==1)?a:e(n-1,a*n);
}
alert(f(5));

比较:
- 线性递归:f(n),返回值会被调用者使用。
- 尾递归:f(m,n),返回值不会被调用者使用。
尾递归由于 直接返回值,不需要保存临时变量,所以性能不会产生线性增加,并且JavaScript解释器会将尾递归形式优化。
