网站设计哪家专业/网络营销软文范例500字
2-1 图的分类
图是一个用线 或 边连接在一起的顶点的集合,可以说,图是有限 顶点V 和 边E 的有序对。顶点(Vertex),边(Edge)
图a中的边没有方向,称为无向图。图b中边存在方向称为有向图。
1.1(a)所示的图可以表示为 G1(V, E)。其中顶点集合 V(G1) = { 1, 2, 3, 4, 5, 6 },集合
中的元素为顶点(用序号代表,在其他图中,顶点集合中的元素也可以是其他标识顶点的符号,
如字母 A、B、C 等);
边的集合为:E(G1) = { (1, 2), (1, 3), (2, 3), (2, 4), (2, 5), (2, 6), (3, 4), (3, 5), (4, 5) }
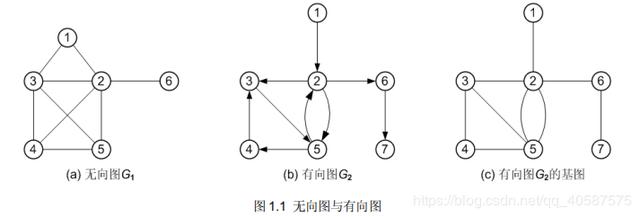
图 1.1(b)所示的图可以表示为 G2(V, E),其中顶点集合 V(G2) = { 1, 2, 3, 4, 5, 6, 7 },集合中的元素也为顶点的序号;
边的集合为:
E(G2) = { <1, 2>, <2, 3>, <2, 5>, <2, 6>, <3, 5>, <4, 3>, <5, 2>, <5, 4>, <6, 7> }。
在上述边的集合中,每个元素为一对顶点构成的有序对(用尖括号括起来),
表示从点 u 到顶点 v 的有向边(directed Edge)
权值(weight):某些图的边具有与它相关的数,称为权值。
下列图示分别表示:无向有权图,有向有权图
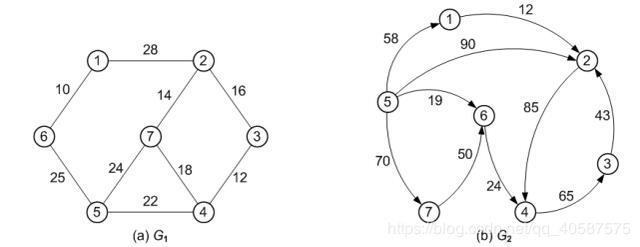
上图a中:所示的无向网可表示为 G1(V, E),其中顶点集合 V(G1) = { 1, 2, 3, 4, 5, 6, 7 };
边的集合为:
E(G1) = { (1, 2, 28), (1, 6, 10), (2, 3, 16), (2, 7, 14), (3, 4, 12), (4, 5, 22), (4, 7, 18), (5, 6, 25), (5, 7, 24) }。
在边的集合中,每个元素的第 3 个分量表示该边的权值。
所以依据图的有无方向和权值可以分为4类:
1.无向无权图
2.有向无权图
3.无向有权图
4.有向有权图
2-2 图的基本概念
顶点的度(degree):对于无向图来说,一个顶点的度就是这个顶点的相邻的边的数量。如第一张图a中点1的度就是 2 。
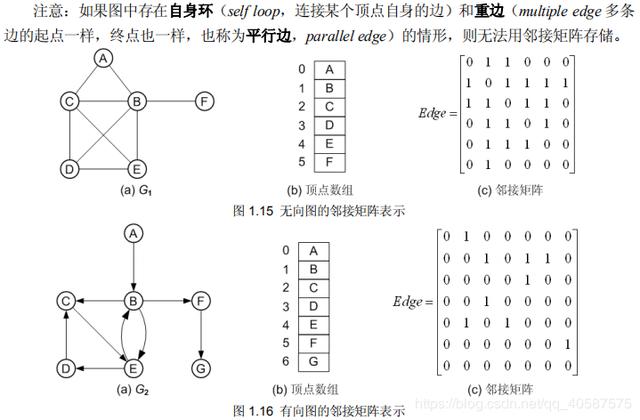
简单图:没有自环边,没有平行边
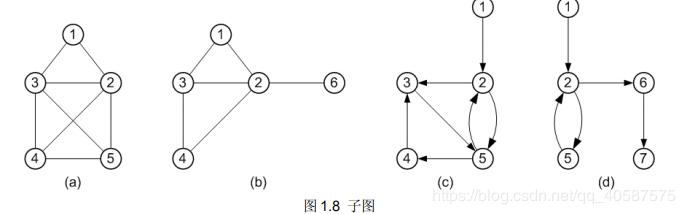
子图:例如,图 1.8(a)、(b)所示的无向图都是图 1.1(a)所示的无向图 G1的子图
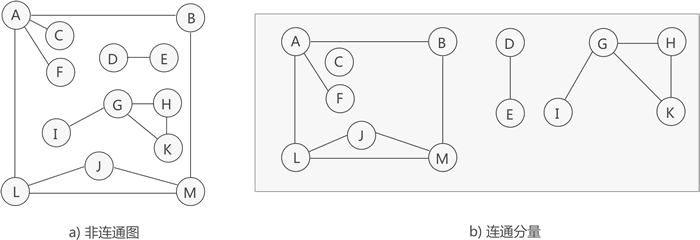
联通图和非联通图:
在无向图中,若从顶点 u 到 v 有路径,则称顶点 u 和 v是连通的(connected)。
如果无向图中任意一对顶点都是连通的,则称此图是连通图(connected graph);
相反,如果一个无向图不是连通图,则称为非连通图(disconnected graph)。
如果一个无向图不是连通的,则其极大连通子图称为连通分量(connected component)
树是一种无环图,任意结点都可以看做是根节点。联通的无环图是树。
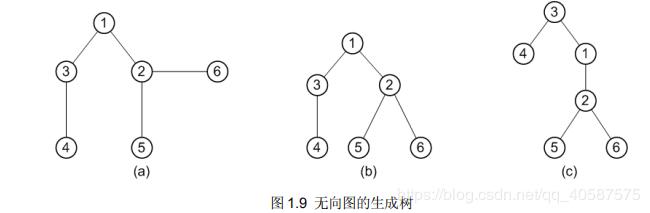
生成树(Spanning Tree):一个无向连通图的生成树是它的包含所有顶点的极小连通子图,这里所谓的极小就是边的数目极小。
如果图中有 n 个顶点,则生成树有 n-1 条边。一个无向连通图可能有多个生成树。
图1.1(a) 所示的无向图 G1的一个生成树如图 1.9(a)所示。为了更形象地表示这个生成树,
在图 1.9 中,图(b)把它画成了以顶点 1 为根结点的树,图(c)把它画成了以顶点 3 为根结点的树。
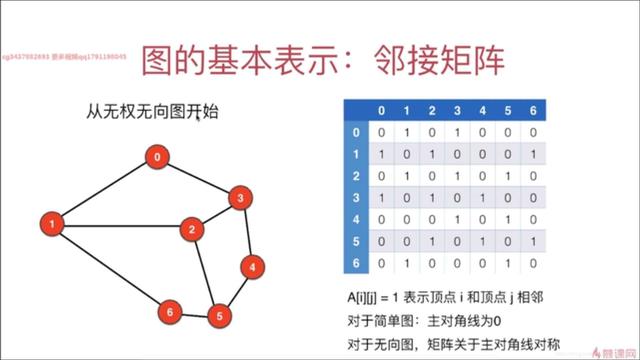
2-3 图的基本表示:邻接矩阵
在邻接矩阵存储方法中,除了一个记录各个顶点信息的顶点数组外,还有一个表示各个顶点
之间关系的矩阵,称为邻接矩阵(adjacency matrix)。两顶点相邻则为1, 不相邻则为 0
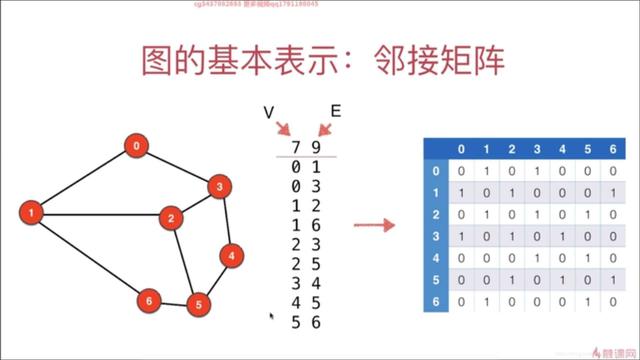
其中 V = 7 表示顶点的数量, E = 9 表示边的数量
欢迎关注工纵号:不止于编程,更多干货。
练习的是简单图,不包含自环边和平行边
java代码实现
import java.io.File;import java.io.IOException;import java.util.ArrayList;import java.util.Scanner;//只是处理简单的图public class AdjMatrix {private int V; // 图的顶点的数量private int E; // 图的边的数量private int[][] adj; // 邻接矩阵public AdjMatrix(String filename) {File file = new File(filename);try {// 读取文件Scanner scanner = new Scanner(file);V = scanner.nextInt();// 判断顶点数量是否有误if (V < 0) throw new IllegalArgumentException("V 必须是个不为负数的数值");adj = new int[V][V]; // 创建二维矩阵E = scanner.nextInt();if (V < 0) throw new IllegalArgumentException("E 必须是个不为负数的数值");for (int i = 0; i< E; i++) {int a = scanner.nextInt();validateVertex(a);int b = scanner.nextInt();validateVertex(b);// 判断是否是自环边if (a == b) throw new IllegalArgumentException("不允许存在自环边");if (adj[a][b] == 1) throw new IllegalArgumentException("不允许存在平行边");adj[a][b] = 1;adj[b][a] = 1;}} catch (IOException e) {e.printStackTrace();}}private void validateVertex(int v) {if (v < 0 || v > V) {throw new IllegalArgumentException("输入的数值" + v +"不合法");}}// 获取指定结点相邻的结点public ArrayList adj(int v){validateVertex(v);ArrayList res = new ArrayList<>();for (int i = 0; i < V; i++) { // 顶点的数量if (adj[v][i] == 1) {res.add(i);}}return res;}// 获取指定结点的度,即相邻的结点的数量public int degree(int v) {return adj(v).size();}public int V() {return V;}public int E() {return E;}public boolean hasEdge(int x, int y) { // 依据两个顶点判断边是否存在validateVertex(x);validateVertex(y);return adj[x][y] == 1;}public String toString() {StringBuilder stringBuilder = new StringBuilder();stringBuilder.append(String.format("V = %d, E = %d ", V, E)); // 打印出矩阵for (int i =0; i< V; i++) {for (int j = 0; j < V; j++) {stringBuilder.append(String.format("%d ", adj[i][j]));}stringBuilder.append("");}return stringBuilder.toString();}public static void main(String[] args) {AdjMatrix adjMatrix = new AdjMatrix("g.txt");System.out.println(adjMatrix);//V = 7, E = 9 //0 1 0 1 0 0 0 //1 0 1 0 0 0 1 //0 1 0 1 0 1 0 //1 0 1 0 1 0 0 //0 0 0 1 0 1 0 //0 0 1 0 1 0 1 //0 1 0 0 0 1 0 System.out.println(adjMatrix.adj(2).toString());System.out.println(adjMatrix.degree(2));}}
欢迎关注工纵号:不止于编程,更多干货。


