集合及其应用

一.集合的概念

何为集合

①不严格定义

​ 看过这篇博客的人可以构成一个集合，通过百度搜索引擎找到这篇博客的人可以构成一个集合，在CSDN内部搜索到这篇博客的人可以构成一个集合，通过关键字搜索遇到这篇博客的人可以构成一个集合，浏览的时候无意间看到这篇博客的人也可以构成一个集合…
​ 在朴素集合论体系中,“ 集合”是一个原始概念， 在朴素集合论中“集合”不能严格定义，直观一点说，把一些事物汇集到一起组成一个整体就称作集合(通常用大写英文字母来标记)，而这些事物就是这个集合的元素。
​ 我们的键盘上就可以找出好多集合：如26个字母键的集合，10个数字键的集合，功能键组成的集合，光标控制键组成的集合等等

​ 集合是最基本的离散结构，其他所有离散结构都建立于集合之上。

②集合与元素关系

​ 集合与其元素就两种关系，要么元素$\in$(属于)集合，要么元素$\notin$（or$\overline{\in }$)（不属于）集合（集合的确定性） ，“属于”其实也是一个原始概念。

③集合的表示方法

（1）列举法

​ 可以想成花名册，要罗列出来.，格式为：列出元素，用逗号隔开，用花括号括起来，如果元素很多，且符合一定常识，可以用" ⋯ " "⋯"来替代一部分。

​ 如：设A是小于5的正整数的集合，则A={1,2,3,4}A=\{1,2,3,4\}A={1,2,3,4}

​ 注意无序性（元素不能重复出现）和互异性（集合中元素无顺序之分），

（2）描述法

​ 就是通过描述作为集合的元素所具有的性质来刻画一个集合，一般形式为：{x∣x具有性质P}\{x|x具有性质P\}{x∣x具有性质P}，读作满足P的所有x的集合

​ 如：还是上面那个例子，设A是小于5的正整数的集合，则A={x∣x是小于5的正整数}A=\{x|x是小于5的正整数\}A={x∣x是小于5的正整数}

（3）两种方法转换

​ 有时可以互相转换，上面所举的例子说明了这一点；而有时候不行，如[0,1]中的所有实数构成的集合就无法用列举法来表示。

二.子集、集合的相等

1. 子集

①定义

​ 设$A$、$B$是两个集合，若$A$中的每个元素都是$B$中的元素，则称$A$是B的子集，记作$A\subseteq B$

​ 还是用前面那段中二的话来表述😆，通过百度搜索引擎找到这篇博客的人可以构成一个集合，在CSDN内部搜索到这篇博客的人可以构成一个集合，这两个集合是看到这篇博客的人所构成的集合的子集

​ 同时，还是前面那个{1,2,3,4}\{1,2,3,4\}{1,2,3,4}的例子，{1,2,3}⊆{1,2,3,4}\{1,2,3\}\subseteq\{1,2,3,4\}{1,2,3}⊆{1,2,3,4}

​

②符号语言

$$\begin{gathered} A\subseteq B⟺\forall x,x\in A\to x\in B \\ orA\subseteq B⟺\forall x\in A,x\in B \\ orA\subseteq B⟺\forall x\notin B\to x\notin A \end{gathered}$$

③“$\subseteq$”的性质

（1）$A\subseteq A$

{1,2,3,4}⊆{1,2,3,4}\{1,2,3,4\}\subseteq\{1,2,3,4\} {1,2,3,4}⊆{1,2,3,4}

（2）如果$A\subseteq B$，且$B\subseteq C$，则$A\subseteq C$

{1,2}⊆{1,2,3},{1,2,3}⊆{1,2,3,4}⟹{1,2}⊆{1,2,3,4}\{1,2\}\subseteq\{1,2,3\},\{1,2,3\}\subseteq\{1,2,3,4\}\Longrightarrow\{1,2\}\subseteq\{1,2,3,4\} {1,2}⊆{1,2,3},{1,2,3}⊆{1,2,3,4}⟹{1,2}⊆{1,2,3,4}

④辨析$\in 和\subseteq$

（1）元素有时也是集合，集合有时也是元素

(2 ) 对于集合A、B，$A\in B$和$A\subseteq B$可能同时成立

​ 如：

​
{a}∈{a,{a}}且{a}⊆{a,{a}}\{a\}\in\{a,\{a\}\}\ \qquad 且\qquad\{a\}\subseteq\{a,\{a\}\} {a}∈{a,{a}} 且{a}⊆{a,{a}}
​ {a}是集合{a,{a}}中的元素，同时它也是由一个元素a构成的集合

2.真子集

①定义

​ 设$A,B$是两个集合，且$A\subseteq B$，$\exists x\in B,x\notin A$,则称A为B的真子集，记作$A\subset B$

②符号语言

​
$$A\subset B⟺A\subseteq B并且\exists x(x\in B并且x\notin A)$$

③“$\subset$”的性质

（1）$A\not\subset A$

{1,2,3,4}⊄{1,2,3,4}\{1,2,3,4\}\not\subset\{1,2,3,4\} {1,2,3,4}​⊂{1,2,3,4}

（2）如果$A\subset B$，且$B\subset C$，则$A\subset C$

{1,2}⊂{1,2,3},{1,2,3}⊂{1,2,3,4}⟹{1,2}⊂{1,2,3,4}\{1,2\}\subset\{1,2,3\},\{1,2,3\}\subset\{1,2,3,4\}\Longrightarrow\{1,2\}\subset\{1,2,3,4\} {1,2}⊂{1,2,3},{1,2,3}⊂{1,2,3,4}⟹{1,2}⊂{1,2,3,4}

（3）$A\subset B$,则$B\not\subset A$

3.集合的相等

①定义

设$A,B$是两个集合，且$A ⊆ B , B ⊆ A $，则称$A$ 与$B$相等，记作$A$ =$B$

②符号语言

$$A=B⟺\forall x(x\in A\leftrightarrow x\in B)$$

③性质

（1）$A\ne B⟺A⊈BorB⊈A$

{1,2,3}≠{1,2,3,4}\{1,2,3\}\ne\{1,2,3,4\} {1,2,3}​={1,2,3,4}

（2）$A\subset B⟺$$A\subseteq B$且$A\ne B$

{1,2,3}⊂{1,2,3,4}⟺{1,2,3}⊆{1,2,3,4}且{1,2,3}≠{1,2,3,4}\{1,2,3\}\subset\{1,2,3,4\}\iff\{1,2,3\}\subseteq\{1,2,3,4\}且\{1,2,3\}\ne\{1,2,3,4\} {1,2,3}⊂{1,2,3,4}⟺{1,2,3}⊆{1,2,3,4}且{1,2,3}​={1,2,3,4}

4.空集

①定义

​ 不拥有任何元素的集合称为空集，记作Ø。

②注意：{∅}\{\emptyset\}{∅}不是空集

③定理

​ 空集是一切集合的子集

推论：空集是唯一的

证明空集唯一（反证法）

$$设\varnothing 和{\varnothing }^{\prime }都是空集，则由空集是一切集合的子集可知，\varnothing \subseteq {\varnothing }^{\prime }且{\varnothing }^{\prime }\subseteq \varnothing ,则\varnothing ={\varnothing }^{\prime },从而空集唯一$$

5.集族

①定义

​ 以集合为元素的集合称为集族

②表示方法

​ 集族的表示方法： 设 A={A1,A2,A3,…An}A=\{A_1,A_2,A_3,… A_n\}A={A1​,A2​,A3​,…An​} 为一个集族，若令 I={1,2,3,…n}I= \{1,2,3,… n\}I={1,2,3,…n} ，则$\forall i\in I,i$ 确定了一个唯一的集合$A_i$,于是集族$A$又常写成{Ah}h∈I\{A_h\}_{h\in I}{Ah​}h∈I​

③例子

​ 大学中，每个学院的学生形成一个集合，全校各个学院就形成一个集族

6.幂集

①定义

​ 集合S的所有子集(包括空集$\varnothing$和S本身）形成的集族称为S的幂集，并记为$2^S$，或记为$P(S)$

​ 2S={A∣A⊆S}2^S=\{A|A\subseteq S\}2S={A∣A⊆S}

②定理(幂集元素个数，集合子集个数)

​ 设集合$A$的元素个数$|A|=n$($n$为自然数)，则$|P(A)|=2^n$(证明：二项式定理)

③注

​ 2Ø={Ø}2^ Ø =\{Ø\}2Ø={Ø} ，$\varnothing$是空集，而{∅}\{\empty\}{∅}是一个集族
∅≠{∅}∅∈{∅}∅⊆{∅}\empty \ne \{\empty\}\quad \empty\in \{\empty\}\quad \empty\subseteq \{\empty\} ∅​={∅}∅∈{∅}∅⊆{∅}

三.集合的基本运算

1.并集

①定义

设$A,B$ 是两个集合,至少属于这两个集合之一的元素构成的集合称为$A$与$B$ 的并集,记作$A\cup B$

公式化表述为A∪B={x∣x∈A或x∈B}A ∪ B = \{ x ∣ x ∈ A 或 x ∈ B \}A∪B={x∣x∈A或x∈B}

②定理(并运算规律)

设$A , B , C $为任意三个集合,则对于并运算,满足以下几个规律:

$1.交换律:A\cup B=B\cup A$
$2.结合律:A\cup (B\cup C)=(A\cup B)\cup C$
$3.幂等律:A\cup A=A$

$4.\varnothing \cup A=A$

$5.A\cup B=B⟺A\subseteq B$

③推广

（1）多个集合的并集

集合的并运算可以推广到多个集合的并集

$A_1\cup A_2\cup ...\cup A_n$ 定义为至少属于$A_1,A_2,...,A_n$ 中之一的那些元素构成的集合,简记为$\underset{i=1}{\overset{n}{\cup }}{A}_i$

若$A_1,A_2,...,A_n,...$是一个集合的无穷序列，则并集可以记为$A_1\cup A_2\cup ...\cup A_n,...$，简记为$\underset{i=1}{\overset{\infty }{\cup }}{A}_i$

（2）集族中元素的并集

一般地, , 若 {Al}l∈I\{A_l\}_{l\in I}{Al​}l∈I​是任一集族, , 则集族中那些集合的并集记为∪l∈IAl={x∣∃l∈I使得x∈Al}\mathop\cup\limits_{l\in I}A_l=\{x|\exists l \in I\ 使得 x\in A_l\}l∈I∪​Al​={x∣∃l∈I 使得x∈Al​}

2.交集

①定义

设$A,B$ 是两个集合,由既属于$A$又属于$B$ 的一切元素构成的集合称为$A$与$B$的交集记作 $A\cap B$

公式化表示为A∩B={x∣x∈A且x∈B}A∩B=\{ x ∣ x ∈ A 且 x ∈ B \}A∩B={x∣x∈A且x∈B}

②定理(交运算规律)

设$A , B , C $为任意三个集合,则对于交运算,满足以下几个规律:

$1.交换律:A\cap B=B\cap A$
$2.结合律:A\cap (B\cap C)=(A\cap B)\cap C$
$3.幂等律:A\cap A=A$

$4.\varnothing \cap A=\varnothing$
$5.A\cap B=A⟺A\subseteq B$

③推广

(1)多个集合的交集

​ 与并运算类似，可将集合的交推广到有限个或可数个集合
A1∩A2∩...∩An=∩i=1nAi={x∣∀i∈{1,2,...,n},x∈Ai}A_1\cap A_2\cap...\cap A_n=\mathop\cap\limits^n_{i=1}A_i=\{x|\forall i\in\{1,2,...,n\},x\in A_i\} A1​∩A2​∩...∩An​=i=1∩n​Ai​={x∣∀i∈{1,2,...,n},x∈Ai​}

A1∩A2∩...∩An∩...=∩i=1∞Ai={x∣∀n∈N,x∈An}A_1\cap A_2\cap...\cap A_n\cap...=\mathop\cap\limits^\infty_{i=1}A_i=\{x|\forall n\in N,x\in A_n\} A1​∩A2​∩...∩An​∩...=i=1∩∞​Ai​={x∣∀n∈N,x∈An​}

(2)集族中元素的交集

一般地, , 若 {Al}l∈I\{A_l\}_{l\in I}{Al​}l∈I​是任一集族, , 则集族中那些集合的交集记为$\underset{l\in I}{\cap }{A}_l$,其定义为∩l∈IAl={x∣∀ξ∈I,x∈Aξ}\mathop\cap\limits_{l\in I}A_l=\{x|\forall \xi \in I,x\in A_{\xi}\}l∈I∩​Al​={x∣∀ξ∈I,x∈Aξ​}

3.交并运算律

①定理：分配律

设$A , B , C $为任意三个集合,则

交运算对并运算满足分配律,$A\cap (B\cup C)=(A\cap B)\cup (A\cap C)$
并运算对交运算满足分配律,$A\cup (B\cap C)=(A\cup B)\cap (A\cup C)$

其实记忆这些分配律就可以用小学学的乘法对加法的分配律来记住

对于集族，也成立：

设$A$为一集合,{Bl}l∈I\{ B_ l \}_{l ∈ I }{Bl​}l∈I​为任一集族，则：
$$\begin{gathered} A\cap (\underset{l\in I}{\cup }{B}_l)=\underset{l\in I}{\cup }(A\cap B_l) \\ A\cup (\underset{l\in I}{\cap }{B}_l)=\underset{l\in I}{\cap }(A\cup B_l) \end{gathered}$$

②定理：吸收律

对任何集合 $A,B$, 吸收律成立:
$$\begin{gathered} A\cap (A\cup B)=A \\ A\cup (A\cap B)=A \end{gathered}$$

证明：
$$\begin{gathered} (P\cup \varnothing )\cap (P\cup Q)=P\cup (\varnothing \cap Q)=P\cup \varnothing =P \\ (P\cap S)\cup (P\cap Q)=P\cap (S\cup Q)=P\cap S=P \end{gathered}$$

4.两两不相交的集序列

定义

设$A,B$ 为任意集合，若$A\cap B=Ø$，则称A, B 不相交。若集序列$A_1,A_2,...,A_n,...$对于任意的$A_i$与$A_j(i\ne j)$不相交,
则称$A_1,A_2,A_n,...$ 是两两不相交的集序列

5.差集

①定义

设$A,B$为两个任意集合，由属于$A$而不属于$B$ 的全体元素组成的集合称为$A$ 与$B$的差集，记作$A\setminus B$

②符号语言

A∖B={x∣x∈A且x∉B}A\setminus B=\{x|x\in A 且x\notin B\} A∖B={x∣x∈A且x∈/​B}

③差运算

（1）定理：交对差的分配律

​ 设$A,B,C$为任意三个集合，则$A\cap (B\setminus C)=(A\cap B)\setminus (A\cap C)$

（2）一般情况下，差运算不满足交换律，不满足结合律

即：一般$A\setminus B\ne B\setminus A(A\setminus B)\setminus C\ne A\setminus (B\setminus C)$

例如

A={1,2,3},B={1,2},C={3}A∖B={3}B∖A=∅(A∖B)∖C=∅A∖(B∖C)={3}A=\{1,2,3\},B=\{1,2\},C=\{3\}\\A\setminus B=\{3\}\qquad B\setminus A=\empty\\(A\setminus B)\setminus C =\empty \qquad A\setminus (B\setminus C)=\{3\}A={1,2,3},B={1,2},C={3}A∖B={3}B∖A=∅(A∖B)∖C=∅A∖(B∖C)={3}

（3）定理：差判定子集

​ 设 $A,B$ 为任意二个集合, 则$(A\setminus B)\cup B=A⟺B\subseteq A$

（4）对称差

定义

设 $A,B$为任意两个集合，称$A\setminus B与B\setminus A$ 的并集称为$A$与$B$的对称差，记作$A\Delta B$( 也记作$A\oplus B$）

AΔB=(A∖B)∪(B∖A)={x∣(x∈A且x∉B)或(x∉A且x∈B}={x∣x∈A∪B且x∉A∩B}=(A∪B)∖(A∩B)A\Delta B=(A\setminus B)\cup(B\setminus A)\\\quad \quad=\{x|(x\in A且x\notin B)或(x\notin A且x\in B\}\\\quad \quad=\{x|x\in A\cup B且x\notin A \cap B\}\\\quad \quad=(A\cup B)\setminus(A\cap B)AΔB=(A∖B)∪(B∖A)={x∣(x∈A且x∈/​B)或(x∈/​A且x∈B}={x∣x∈A∪B且x∈/​A∩B}=(A∪B)∖(A∩B)

性质

$$\begin{gathered} 1.交换律,A\Delta B=B\Delta A \\ 2.结合律,A\Delta (B\Delta C)=(A\Delta B)\Delta C \\ 3.交运算关于对称差满足分配律,即A\cap (B\Delta C)=(A\cap B)\Delta (A\cap C) \\ 4.A\Delta \varnothing =A \\ 5.A\Delta A=\varnothing \end{gathered}$$

四.余集、DE Morgan公式

1.全集

①概念

一般的，如果一个集合含有我们所研究问题中涉及的所有元素，那么就称这个集合为全集

②性质

​ 任何集合都可以看做是全集，包括空集

③文氏图

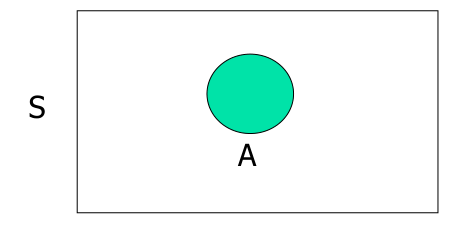
2.余集

①定义

设$S$ 是一个集合 ,$A\subseteq S$, 差集$S\setminus A$ 称为集$A$ 对集$S $的余集（也称为补集）
记为 $A^c$ 或$C_{S}A$或$\overline{A}$ 即$A^c=S\setminus A$

②文氏图表示

③性质

设$A\subseteq S$,则有下述结论.

$1.S对S的余集为空集,即C_{S}S=S^c=\varnothing$

$2.{\varnothing }^c=S(C_S\varnothing =S)$.
$3.A\cap A^c=\varnothing$
$4.A\cup A^c=S$
若$A、B\subseteq S$则$A^c=B$当且仅当$A\cap B=\varnothing$ 并且$A\cup B=S$

3.De Morgan 公式

①定理：并集的余集等于各余集的交集

$$(\underset{\xi \in I}{\cup }{A}_{\xi }{)}^c=\underset{\xi \in I}{\cap }{A}_{\xi }^c$$

②定理：交集的余集等于各余集的并集

$$(\underset{\xi \in I}{\cap }{A}_{\xi }{)}^c=\underset{\xi \in I}{\cup }{A}_{\xi }^c$$

定理①、②中若集合数为2，可得到

$(A\cup B{)}^c=A^c\cap B^c$

$(A\cap B{)}^c=A^c\cup B^c$

③定理（余集、差集、对称差之间的联系）

​ $A\setminus B=A\cap B^c$

​ $A\Delta B=(A\cap B^c)\cup (B\cap A^c)$

​ $A^c=S\Delta A$

五.笛卡尔乘积

1.有序对

​ 两个对象a 和 b( 允许 a=b) 按 一定的次序排列 的整体叫做一个二元组或有序对。

​ 规定 (a,b)=(c,d) 当且仅当 a=c,b=d

注：此系列博客用{a,b}{b,a}表示无序对，（a,b)表示有序对（参考教材为《离散数学引论》哈尔滨工业大学出版社），其他教材上有的用（a,b)表示无序对，<a,b>表示有序对

2.笛卡尔积

①定义

设$A$ 与$B$ 为任意两个集合, , 则称集合{(a,b)∣a∈A且b∈B}\{( a,b) | a\in A 且b \in B \}{(a,b)∣a∈A且b∈B}为$A$与$B$的笛卡尔乘积, , 记为$A\times B$

A×B={(a,b)∣a∈A且b∈B}A\times B=\{( a,b) | a\in A 且b \in B \}A×B={(a,b)∣a∈A且b∈B}

由定义可知，对任一集合$A$ ，有：$A\times \varnothing =\varnothing \times A=\varnothing$

②两个集合笛卡尔积的元素个数

对任意有穷集合$Ａ,B,$ 如果用$|A|,|B|$ 分别表示Ａ和B 中元素的个数，那么$|A\times B|＝|A|\times |B|$。

③定理：笛卡尔积的集合运算律

一般情况下笛卡尔积不满足交换律，即$A\times B\ne B\times A$

设$A,B,C$为任意三个集合，则笛卡尔积运算对并、交差运算分别满足分配律，即：
$$\begin{gathered} A\times (B\cup C)=(A\times B)\cup (A\times C) \\ A\times (B\cap C)=(A\times B)\cap (A\times C) \\ A\times (B\setminus C)=(A\times B)\setminus (A\times C) \end{gathered}$$

④笛卡尔积的扩展

​ 有序对也叫二元组, 二元组可推广到三元组, 四元组,一直到n元组。
​ 三元组就是三个元素按一定次序组成的整体，设第一个元素为x, 第二个元素为y, 第三个元素为z, 则这个三元组就
记为(x,y,z)。

​ 一般地，一个n 元组就是n 个元素按一定次序组成的整体，设第一个元素为$x_1$ , 第二个元素为$x_2$ ,…, 第n 个元素
为 为$x_n$ , 则这个n 元组就记为$(x_1,x_2,...,x_n)$
称两个n 元组$(x_1,x_2,...,x_n)$与$(y_1,y_2,...,y_n)$ 相等当且仅当 $x_1＝y_1,x_2＝y_2,...,x_n=y_n$。
设$A_1,A_2,...,A_n(n\ge 2)$ 为n个集合，集合{(a1,a2,...,an)∣ai∈Ai,i=1,2,...,n}\{(a_1,a_2 , ..., a_n)|a_i\in A_i,i=1,2,...,n\}{(a1​,a2​,...,an​)∣ai​∈Ai​,i=1,2,...,n}称为$A_1,A_2,...,A_n$的笛卡尔乘积,并记为: $A_1\times A_2\times ...\times A_n$。
当 $A_1=A_2=...=A_n=A$时，$A_1\times A_2\times ...\times A_n$。 就简记为 $A^n$ 。

六.有穷集合的基数

1.一一对应

①定义

​ 设$A$ 和$B$是两个集合, 如果有一个法则$\phi$ 使$\forall x\in A$, 根据法则$\phi$ 在$Ｂ$中有唯一的一个$y$与$x$对应，这个$y$常记为$\phi (x)$, 而且$y\in B$, 在$A $中也有唯一的一个$x $使$x $在$\varphi$下对应于$y $。这个法则称为从$A$ 到$B$的一个一一对应

②性质

​ 若集合$A$ 和集合$B$ 之间存在一一对应，则$|A|=|B|$

③定义（一一对应与笛卡尔积关系）

一个集合$A$ 到集合$B$的一一对应是$A\times B$ 的子集$\phi$ 使之满足：
(1)$\forall x\in A,\exists y\in B$ 使 $(x,y)\in \phi$ 如果$(x,y),(x,z)\in \phi$, 则 y=z
(2)$\forall y\in B,\exists x\in A$ 使得 $(x,y)\in \phi$ ; 并且如果$(x,y)、(x^{\prime },y)\in \phi$, , 则$x=x^{\prime }$。
如果 $(x,y)\in \phi$ ，则把$y记为\phi (x)$, 即 $y=\phi (x)$

④定义（有限集）

​ 集合A称为有限集，若存在一个自然数n使得A与集合{1,2,...,n}\{1,2,...,n\}{1,2,...,n}间存在一个一一对应。数n称为A的基数

（1）A为空集

​ 基数n=0

（2）A不是空集

​ A的基数为|A|

​ 若A不是有穷集，则称A为无穷集

⑤定义（|A|<|B|)

​ 若A与B的一个真子集间有一个一一对应存在，但A与B之间不存在一一对应，则称|A|<|B|,记为|A|<|B|，

2.容斥原理

①定理（加法法则）

(1)两个有限集

​ 设$A,B$为两个不相交的有限集，则$|A\cup B|=|A|+|B|$

（2）多个有限集

​ 设$A_1,A_2,...,A_n$为$n$个两两不相交的有限集，则：$|\underset{i=1}{\overset{n}{\cup }}{A}_i|=\underset{i=1}{\overset{n}{\Sigma }}{A}_i$

②定理（乘法法则）

(1)两个有限集

​ 设$A,B$为两个不相交的有限集，则$|A\times B|=|A|\cdot |B|$

（2）多个有限集

设$A_1,A_2,...,A_n$为$n$个两两不相交的有限集，则：$|B_1\times B_2\times ...\times B_n|=|B_1|\cdot |B_2|\cdot ...|B_n|$

③定理（减法法则与淘汰原理）

​ 设$S$为有穷集，$A\subseteq S$,则$|A^c|=|S|-|A|$

④定理（并运算）

​ 设$A,B$为两个有限集，则$|A\cup B|=|A|+|B|-|A\cap B|$

⑤定理（对称差运算）

​ 设$A,B$为两个有限集，则$|A\Delta B|=|A|+|B|-2|A\cap B|$

⑥定理（逐步淘汰原理or容斥原理）

​ 设$A_1,A_2,...A_n为n$个有穷集，则：

（1）形式一

$$|\underset{i=1}{\overset{n}{\cup }}{A}_i|=\sum _{i=1}^n|A_i|-\sum _{1\le i<j\le n}^n|A_i\cap A_j|+\sum _{1\le i<j<k\le n}^n|A_i\cap A_j\cap A_k|-...+(-1{)}^{n-1}|A_1\cap A_2\cap ...\cap A_n|$$

（2）形式二

$$|\underset{i=1}{\overset{n}{\cap }}{A}_i|=|S|-\sum _{i=1}^n|A_i|+\sum _{1\le i<j\le n}^n|A_i\cap A_j|-\sum _{1\le i<j<k\le n}^n|A_i\cap A_j\cap A_k|+...+(-1{)}^n|A_1\cap A_2\cap ...\cap A_n|$$

由上可得：
$$|\underset{i=1}{\overset{n}{\cap }}{A}_i|=|S|-|\underset{i=1}{\overset{n}{\cup }}{A}_i|$$

（1）形式一

$$|\underset{i=1}{\overset{n}{\cup }}{A}_i|=\sum _{i=1}^n|A_i|-\sum _{1\le i<j\le n}^n|A_i\cap A_j|+\sum _{1\le i<j<k\le n}^n|A_i\cap A_j\cap A_k|-...+(-1{)}^{n-1}|A_1\cap A_2\cap ...\cap A_n|$$

（2）形式二

$$|\underset{i=1}{\overset{n}{\cap }}{A}_i|=|S|-\sum _{i=1}^n|A_i|+\sum _{1\le i<j\le n}^n|A_i\cap A_j|-\sum _{1\le i<j<k\le n}^n|A_i\cap A_j\cap A_k|+...+(-1{)}^n|A_1\cap A_2\cap ...\cap A_n|$$

由上可得：
$$|\underset{i=1}{\overset{n}{\cap }}{A}_i|=|S|-|\underset{i=1}{\overset{n}{\cup }}{A}_i|$$