温江做网站哪家好搜索引擎排名优化方案

Description

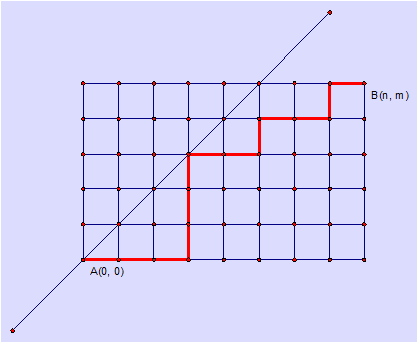
某城市的街道呈网格状，左下角坐标为A(0, 0)，右上角坐标为B(n, m)，其中n >= m。现在从A(0, 0)点出发，只能沿着街道向正右方或者正上方行走，且不能经过图示中直线左上方的点，即任何途径的点(x, y)都要满足x >= y，请问在这些前提下，到达B(n, m)有多少种走法。

 

题解

• 从(0,0)到(n,m)随便走的方案数为C(n+m,m)
• 然后题目要求不能穿过y=x这条直线，也就是不能碰到y=x+1的直线
• 那么我们考虑将一条不合法的路线沿着y=x+1对称过去，那么(n,m)对称过去的点就是(m-1,n+1)
• 考虑Catalan数的证明过程，发现从原点走到对称点(m-1,n+1)的一条路径都可以对称回来，并对应着一条从原点走到终点(n,m)穿过y=x的直线的路径
• 所以穿过y=x的路径数就是从原点走向对称终点的路径是也就是C(n+1+m-1,m-1)=C(n+m,m-1)
• 所有答案就是C(n+m,m)=C(n+m,m-1)
• 可以把式子化简一下：
• 
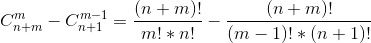
• 通分后得：
• 
• 最后打个高精度就ok了

 

代码

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int N=10000,M=N*10;
struct num
{
    int shu[N];
    friend num operator-(num y,num z) 
    {
        num x;memset(x.shu,0,sizeof(x.shu)),x.shu[0]=y.shu[0];
        for (int i=1;i<=x.shu[0];i++) 
        {
            x.shu[i]+=y.shu[i]-z.shu[i];
            if (x.shu[i]<0) x.shu[i]+=M,x.shu[i+1]--;
        }
        while (!x.shu[x.shu[0]]) x.shu[0]--;
        return x;
    }
    friend num operator*(num y,int z) 
    {
        num x;memset(x.shu,0,sizeof(x.shu)),x.shu[0]=y.shu[0];
        for (int i=1;i<=x.shu[0];i++) x.shu[i]+=y.shu[i]*z,x.shu[i+1]+=x.shu[i]/M,x.shu[i]%=M;
        while (x.shu[x.shu[0]+1]) x.shu[0]++;
        return x;
    }
}ans;
int p[N+5],c[N+5],n,m;
void recout(int x,int f) { for(;x!=1;x/=p[x]) c[p[x]]+=f; }
num C(int m,int n) 
{
    num x;memset(x.shu,0,sizeof(x.shu)),x.shu[0]=x.shu[1]=1,memset(c,0,sizeof(c));
    for (int i=n+1;i<=m;i++) recout(i,1);
    for (int i=1;i<=m-n;i++) recout(i,-1);
    for (int i=1;i<=N;i++) for (int j=1;j<=c[i];j++) x=x*i;
    return x;
}
int main() 
{
    for (int i=2;i<=N;i++) if (!p[i]) for (int j=1;j<=N/i;j++) p[i*j]=i;
    scanf("%d%d",&n,&m),ans=C(m+n,m)-C(m+n,m-1),printf("%d",ans.shu[ans.shu[0]]);
    for (int i=ans.shu[0]-1;i>=1;i--) printf("%05d",ans.shu[i]);
}